Giải phương trình: x2+3y2+2xy-18(x+y)=73
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TL
2
7 tháng 8 2023
a) \(x^4+8x+63\)
\(=x^4+4x^3+9x^2-4x^3-16x^2-36x+7x^2+28x+63\)
\(=x^2\left(x^2+4x+9\right)-4x\left(x^2+4x+9\right)+7\left(x^2+4x+9\right)\)
\(=\left(x^2+4x+9\right)\left(x^2-4x+7\right)\)
7 tháng 8 2023
c) \(\left(x^2+2x+7\right)+\left(x^2-2x+4\right)\left(x^2+2x+3\right)\left(1\right)\)
Ta có : \(x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)
\(\Rightarrow x^2+2x+4=\dfrac{x^3-8}{x-2}\)
\(\left(1\right)\Rightarrow\left[\left(\dfrac{x^3-8}{x-2}+3\right)\right]+\left(x^2-2x+4\right)\left[\left(\dfrac{x^3-8}{x-2}-1\right)\right]\)
\(=\left[\left(\dfrac{x^3-3x-14}{x-2}\right)\right]+\left(x^2-2x+4\right)\left[\left(\dfrac{x^3-2x-5}{x-2}\right)\right]\)
\(=\dfrac{1}{x-2}\left[x^3-3x-14+\left(x^2-2x+4\right)\left(x^3-2x-5\right)\right]\)
6 tháng 8 2023
A= 8x3 - 12x2y + 12xy2 - y3 + 12x2 - 12xy + 3y2 + 6x - 3y + 11
Ta có:
8x3 - 12x2y + 12xy2 - y3 = (2x - y)3 = 93 = 729
12x2 - 12xy + 3y2 = 4x2 - 4xy + y2 + 8x2 - 8xy + 2y2
= (2x - y)2 + 2 (4x2 - 4xy + y2)
= (2x - y)2 + 2(2x - y)2
= 92 + 2.92
= 243
6x - 3y = 3(2x - y) = 3.9 = 27
Vậy A= 8x3 - 12x2y + 12xy2 - y3 + 12x2 - 12xy + 3y2 + 6x - 3y + 11 = 729 + 243 + 27 =999
HQ
Hà Quang Minh
Giáo viên
6 tháng 8 2023
\(2,\left(x+3\right)^2-\left(x+3\right)\left(x-3\right)-6\left(x+1\right)+2050y\\ =x^2+6x+9-x^2+9-6x-6+2050y\\ =2050y+12\\ 3,\left(x+y\right)\left(x^2-xy+y^2\right)+\left(x-y\right)\left(x^2+xy+y^2\right)-2x^3\\ =x^3+y^3+x^3-y^3-2x^3\\ =0\)
6 tháng 8 2023
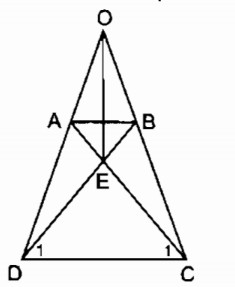
a ) Xét Δ∆ADC và Δ∆BCD, ta có:
AD = BC (tính chất hình thang cân)
∠∠(ADC) = ∠∠(BCD) (gt)
DC chung
Do đó: Δ∆ADC = Δ∆BCD (c.g.c) ⇒ ∠C1∠�1= ∠D1∠�1
Trong Δ∆OCD ta có: ∠C1∠�1= ∠D1∠�1 ⇒ Δ∆OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
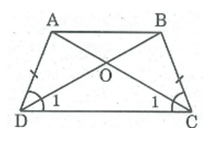
ADC=ˆBCD(gt)⇒ˆODC=ˆOCD���^=���^(��)⇒���^=���^
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
⇒ˆD1=ˆC1⇒�^1=�^1
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
E≢ O. Vậy OE là đường trung trực của AB.
HQ
Hà Quang Minh
Giáo viên
6 tháng 8 2023
Bài 5:
\(3,\left(-a-b\right)^2\\ =\left(-1\right)^2\cdot\left(a+b\right)^2\\ =1\cdot\left(a+b\right)^2\\ =\left(a+b\right)^2\\ 4,\left(a+b\right)^3+\left(a-b\right)^3\\ =\left(a+b+a-b\right)\left[a^2+2ab+b^2-\left(a+b\right)\left(a-b\right)+a^2-2ab+b^2\right]\\ =2a\left(2a^2+2b^2-a^2+b^2\right)\\ =2a\left(a^2+3b^2\right)\)
\(5,\left(3x+2y\right)\left(3x-2y\right)-\left(x+y\right)\left(x-y\right)\\ =9x^2-4y^2-x^2+y^2\\ =8x^2-3y^2\)
AH
Akai Haruma
Giáo viên
6 tháng 8 2023
Bài 5:
3.
$(-a-b)^2=[-(a+b)]^2=(-1)^2(a+b)^2=(a+b)^2$
4. $(a+b)^3+(a-b)^3=(a^3+3a^2b+3ab^2+b^3)+(a^3-3a^2b+3ab^2-b^3)$
$=2a^3+6ab^2=2a(a^2+3b^2)$
5.
$(3x+2y)(3x-2y)-(x+y)(x-y)=(9x^2-4y^2)-(x^2-y^2)=9x^2-4y^2-x^2+y^2=8x^2-3y^2$
Bài 6:
3. $29,9.30,1=(30-0,1)(30+0,1)=30^2-0,1^2=900-0,01=899,99$
4. $31,8^2-2.31,8.21,8+21,8^2+68.66=(31,8-21,8)^2+68.66$
$=10^2+4488=100+4488=4588$
5. $144^2+44^2-288.44=144^2+44^2-2.144.44=(144-44)^2=100^2=10000$
\(x^2+3y^2+2xy-18\left(x+y\right)=73\)
\(\Leftrightarrow x^2+3y^2+2xy-18x-18y-73=0\)
\(\Leftrightarrow x^2-2\left(9-y\right)x+3y^2-18y-73=0\)
\(\Delta'=\left(9-y\right)^2-\left(3y^2-18y-73\right)\)
\(=81-18y+y^2-3y^2+18y+73\)
\(=-2y^2+154\)
\(=-2\left(y^2-77\right)\)
Phương trình có nghiệm khi \(\)
\(\Delta'\ge0\Leftrightarrow-2\left(y^2-77\right)\ge0\Leftrightarrow y^2-77\le0\)
\(\Leftrightarrow y^2\le77\Leftrightarrow-\sqrt[]{77}\le y\le\sqrt[]{77}\)
Phương trình có 2 nghiệm là
\(\left[{}\begin{matrix}x_1=9-y+\sqrt[]{-2\left(y^2-77\right)}\\x_2=9-y-\sqrt[]{-2\left(y^2-77\right)}\end{matrix}\right.\) \(\left(-\sqrt[]{77}\le y\le\sqrt[]{77}\right)\)