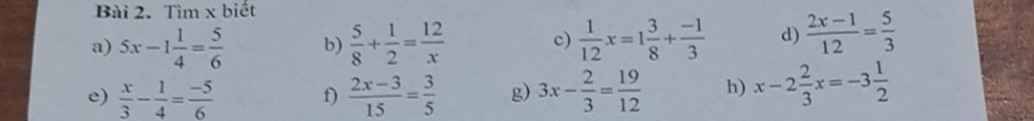 giusp em bai nay em cam on ah
giusp em bai nay em cam on ah
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b; \(\dfrac{2}{3}\) + \(\dfrac{5}{6}\): 5 - \(\dfrac{1}{18}\).(-3)2
= \(\dfrac{2}{3}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{18}\).9
= \(\dfrac{5}{6}\) - \(\dfrac{1}{2}\)
= \(\dfrac{1}{3}\)
c; \(\dfrac{1}{2}\) + \(\dfrac{-1}{6}\) + \(\dfrac{-1}{12}\) + \(\dfrac{-1}{20}\) + \(\dfrac{-1}{30}\) + \(\dfrac{-1}{42}\)
= \(\dfrac{1}{2}\) - (\(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\))
= \(\dfrac{1}{2}\) - (\(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}-\dfrac{1}{7}\))
= \(\dfrac{1}{2}\) - (\(\dfrac{1}{2}\) - \(\dfrac{1}{7}\))
= \(\dfrac{1}{2}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{7}\)
= \(\dfrac{1}{7}\)

Vì A là trung điểm của OM nên
OM = 2OA = 7 x 2 = 14 (cm)
Vì B là trung điểm của ON nên
ON = 2OB = 11 x 2 = 22 (cm)
MN = ON - OM = 22 - 14 = 8 (cm)
Bạn tham khảo:
Để tính độ dài MN, ta sử dụng định lí về trung điểm:
Nếu A là trung điểm của OM và B là trung điểm của ON, thì AB sẽ là đường chính giữa của hình chữ nhật O AMN. Vì AB là đường chính giữa, nên AB sẽ cắt MN tại trung điểm C.
Do đó, ta có MN = 2 X MC
Ta cần tính độ dài MC. Vì M là trung điểm của OA, nên MC = 1/2 OA
Từ đây, ta có:
MC = 1/2 OA = 1/2 7cm = 3.5cm
Do đó:
MN = 2 x MC = 2 x 3.5 = 7cm
Vậy, độ dài MN là 7cm
#hoctot

\(M=1+2.\left(\dfrac{3}{2.5}+\dfrac{5}{5.10}+\dfrac{7}{10.17}+\dfrac{9}{17.26}\right)\)
\(=1+2\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{17}+\dfrac{1}{17}-\dfrac{1}{26}\right)\)
\(=1+2\left(\dfrac{1}{2}-\dfrac{1}{26}\right)\)
\(=1+1-\dfrac{1}{13}=\dfrac{25}{13}\)

Đặt \(A=\dfrac{1}{2^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}\)
\(=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\right)\)
Đặt \(B=1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{50^2}< \dfrac{1}{49\cdot50}=\dfrac{1}{49}-\dfrac{1}{50}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
=>\(B=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}< 2-\dfrac{1}{50}\)
=>\(A=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\right)< \dfrac{1}{2^2}\left(2-\dfrac{1}{50}\right)=\dfrac{1}{2}-\dfrac{1}{200}< \dfrac{1}{2}\)
\(\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{4}\right)^2+\left(\dfrac{1}{6}\right)^2+...+\left(\dfrac{1}{100}\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}.\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}.\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{2}.\dfrac{1}{50}\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2.\left[1+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{50}\right)^2\right]\)
Ta có:
\(\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2.2}< \dfrac{1}{2.1}=\dfrac{2-1}{2.1}=\dfrac{2}{2.1}-\dfrac{1}{2.1}=1-\dfrac{1}{2}\)
\(\left(\dfrac{1}{3}\right)^2=\dfrac{1}{3.3}< \dfrac{1}{3.2}=\dfrac{3-2}{3.2}=\dfrac{3}{3.2}-\dfrac{2}{3.2}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\left(\dfrac{1}{50}\right)^2=\dfrac{1}{50.50}< \dfrac{1}{50.49}=\dfrac{50-49}{50.49}=\dfrac{50}{50.49}-\dfrac{49}{50.49}=\dfrac{1}{49}-\dfrac{1}{50}\)
Khi đó
\(1+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{50}\right)^2< 1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}=2-\dfrac{1}{50}< 2\)
\(=\left(\dfrac{1}{2}\right)^2.\left[1+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{50}\right)^2\right]< \dfrac{1}{4}.2=\dfrac{1}{2}\)
Vậy \(\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{4}\right)^2+\left(\dfrac{1}{6}\right)^2+...+\left(\dfrac{1}{100}\right)^2< \dfrac{1}{2}\left(đpcm\right)\)
Tick cho mk nha :>>



A = \(\dfrac{n+4}{3n+5}\) (n \(\ne\) - \(\dfrac{5}{3}\))
A \(\in\) Z ⇔ n + 4 \(⋮\) 3n + 5
3(n + 4) ⋮ 3n + 5
3n + 12 ⋮ 3n + 5
3n + 5 + 7 ⋮ 3n + 5
7 ⋮ 3n + 5
3n + 5 \(\in\) Ư(7) = {-7; -1; 1; 7}
Lập bảng ta có:
| 3n + 5 | - 7 | - 1 | 1 | 7 |
| n | - 4 | - 2 | - \(\dfrac{4}{3}\) | \(\dfrac{2}{3}\) |
| A = \(\dfrac{n+4}{3n+5}\) | 0 | - 2 | \(\dfrac{8}{3}\) | \(\dfrac{2}{3}\) |
| A \(\in\) Z | loại | loại |
Theo bảng trên ta có n \(\in\) {-4; - 2}
Kết luận A = \(\dfrac{n+4}{3n+5}\) có giá trị nguyên khi và chi khi n \(\in\) {- 4; - 2}
Ta có:
Để \(\dfrac{n+4}{3n+5}\) đạt giá trị nguyên thì \(\left(n+4\right)⋮\left(3n+5\right)\)
\(\Rightarrow3\left(n+4\right)⋮3n+5\)
\(\Rightarrow\left(3n+5+7\right)⋮\left(3n+5\right)\)
\(\Rightarrow7⋮\left(3n+5\right)\)
\(\Rightarrow3n+5\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow3n\in\left\{-12;-6;-4;2\right\}\)
\(\Rightarrow n\in\left\{-4;-2;-\dfrac{4}{3};\dfrac{2}{3}\right\}\)
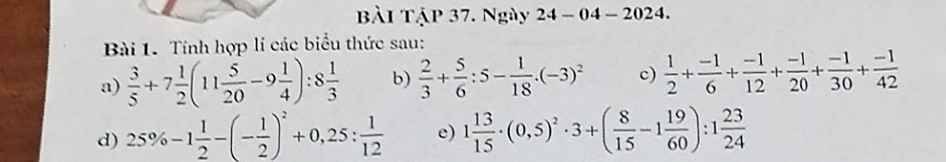
d; \(\dfrac{2x-1}{12}\) = \(\dfrac{5}{3}\)
2\(x\) - 1 = \(\dfrac{5}{3}\).12
2\(x\) - 1 = 20
2\(x\) = 20 + 1
2\(x\) = 21
\(x\) = 21 : 2
\(x=\dfrac{21}{2}\)
Vậy \(x=\dfrac{21}{2}\)
e; \(\dfrac{x}{3}\) - \(\dfrac{1}{4}\) = \(\dfrac{-5}{6}\)
\(\dfrac{x}{3}\) = \(\dfrac{-5}{6}\) + \(\dfrac{1}{4}\)
\(\dfrac{x}{3}\) = - \(\dfrac{7}{12}\)
\(x\) = - \(\dfrac{7}{12}\) x 3
\(x\) = - \(\dfrac{7}{4}\)
Vậy \(x\) = - \(\dfrac{7}{4}\)