
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{1}{3^6}=\dfrac{1}{3^4\cdot3^2}=\dfrac{1}{81\cdot9}=\dfrac{1}{729}\)
\(\dfrac{1}{3^6}\) = \(\dfrac{1}{3^4.3^2}\) = \(\dfrac{1}{81.9}\) = \(\dfrac{1}{729}\)

Bài 2:
a: \(27^{11}=\left(3^3\right)^{11}=3^{33};81^8=\left(3^4\right)^8=3^{32}\)
mà 33>32
nên \(27^{11}>81^8\)
b: \(625^5=\left(5^4\right)^5=5^{20};125^7=\left(5^3\right)^7=5^{21}\)
mà 20<21
nên \(625^5< 125^7\)
c: \(3^{2n}=\left(3^2\right)^n=9^n;2^{3n}=\left(2^3\right)^n=8^n\)
mà 9>8
nên \(3^{2n}>2^{3n}\)
Bài 3:
a: \(3^{1234}=\left(3^2\right)^{617}=9^{617};2^{1851}=\left(2^3\right)^{617}=8^{617}\)
mà 9>8
nên \(3^{1234}>2^{1851}\)
b: \(6^{30}=\left(6^2\right)^{15}=36^{15}>12^{15}\)
c: \(5^{36}=\left(5^3\right)^{12}=125^{12};11^{24}=\left(11^2\right)^{12}=121^{12}\)
mà 125>121
nên \(5^{36}>11^{24}\)
d: \(6^3=6\cdot6^2< 7\cdot6^2\)


\(\widehat{C}=\widehat{B}+10^0=\widehat{A}+10^0+10^0=\widehat{A}+20^0\)
\(\widehat{D}=\widehat{C}+10^0=\widehat{A}+20^0+10^0=\widehat{A}+30^0\)
Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{A}+\widehat{A}+10^0+\widehat{A}+20^0+\widehat{A}+30^0=360^0\)
=>\(4\cdot\widehat{A}=300^0\)
=>\(\widehat{A}=75^0\)
\(\widehat{B}=75^0+10^0=85^0\)
\(\widehat{C}=75^0+20^0=95^0\)
\(\widehat{D}=75^0+30^0=105^0\)

a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{C}+\widehat{D}=360^0-110^0-70^0=180^0\)
=>\(\dfrac{1}{3}\cdot\widehat{D}+\widehat{D}=180^0\)
=>\(\dfrac{4}{3}\cdot\widehat{D}=180^0\)
=>\(\widehat{D}=135^0\)
\(\widehat{C}=\dfrac{1}{3}\cdot135^0=45^0\)
b:
Sửa đề: Cho tứ giác ABCD.
Đặt \(\widehat{B}=x;\widehat{C}=y;\widehat{D}=z\)
\(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)
=>\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(x+y+z=360^0-90^0=270^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{270}{9}=30^0\)
=>\(x=2\cdot30^0=60^0;y=3\cdot30^0=90^0;z=4\cdot30^0=120^0\)
Vậy: \(\widehat{B}=x=60^0;\widehat{C}=y=90^0;\widehat{D}=z=120^0\)

\(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\)

\(\left(-5\right)^5=\left(-5\right)^4\cdot\left(-5\right)=5^4\cdot\left(-5\right)=625\cdot\left(-5\right)=-3125\)


\(\left(x^2-1\right)\left(x^2+2\right)< 0\)
mà \(x^2+2>0\forall x\)
nên \(x^2-1< 0\)
=>\(x^2< 1\)
=>-1<x<1

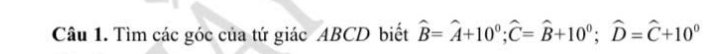
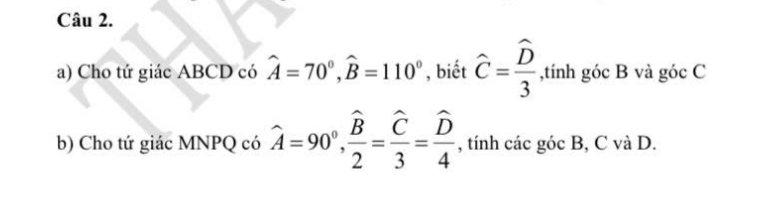
bài 3:
105,7-477:36
=105,7-13,25
=92,45
26,84:22+67,49:17
=1,22+3,97
=5,19
6,58:28x3,02
=0,235x3,02
=0,7097
Bài 4:
13,1:100=0,131; 13,1x0,01=0,131
Do đó: 13,1:100=13,1x0,01
43,05x0,1=4,305; 43,05x0,01=0,4305
Do đó: 43,05x0,1>43,05x0,01
6,33:10=0,633; 6,33x0,01=0,0633
Do đó: 6,33:10>6,33x0,01