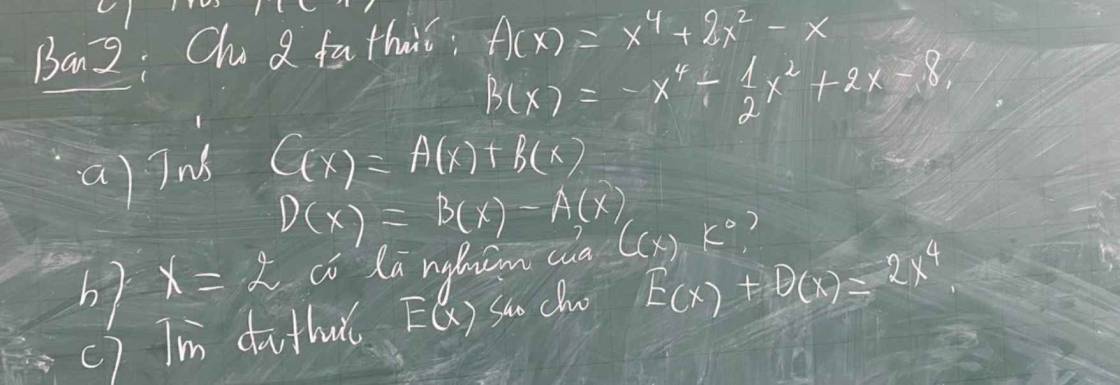 giúp mình vs cần gấp
giúp mình vs cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: DE\(\perp\)AC
AB\(\perp\)AC
Do đó: DE//AB
=>\(\widehat{CHE}=\widehat{CBA}=65^0\)
b: Sửa đề: ΔBAD cân
Xét ΔBIA vuông tại I và ΔBID vuông tại I có
BI chung
IA=ID
Do đó; ΔBIA=ΔBID
=>BA=BD
=>ΔBAD cân tại B
c: Xét ΔCAD có
CI,DE là các đường cao
CI cắt DE tại H
Do đó: H là trực tâm của ΔCAD
=>AH\(\perp\)CD

\(\left(x-5\right)\left(x+1\right)-x\left(x-7\right)=2x+1\)
\(\Leftrightarrow x^2+x-5x-5-\left(x^2-7x\right)=2x+1\)
\(\Leftrightarrow x^2-4x-5-x^2+7x=2x+1\)
\(\Leftrightarrow-4x+7x-2x=1+5\)
\(\Leftrightarrow x=6\)

a.
\(P\left(x\right)=5x^4+x^3+4x^2+4x-6\)
\(P\left(x\right)\) có bậc 4, hệ số cao nhất là 5 và hệ số tự do là -6
\(Q\left(x\right)=-5x^4-x^3-4x^2-3x+2\)
Q(x) có bậc 4, hệ số cao nhất là -5, hệ số tự do là 2
b.
\(M\left(x\right)-P\left(x\right)=Q\left(x\right)\Rightarrow M\left(x\right)=P\left(x\right)+Q\left(x\right)\)
\(\Rightarrow M\left(x\right)=x-4\)
c.
\(M\left(x\right)=0\Rightarrow x-4=0\)
\(\Rightarrow x=4\)
Vậy \(x=4\) là nghiệm của đa thức M(x)

Do tam giác ABC đều và G là trọng tâm nên \(\widehat{AGB}=\widehat{BGC}=\widehat{CGA}\)
Mà \(\widehat{AGB}+\widehat{BGC}+\widehat{CGA}=360^0\)
\(\Rightarrow3\widehat{BGC}=360^0\)
\(\Rightarrow\widehat{BGC}=120^0\)

\(x^3\) + \(x^2\) + 7x
Ta có:
P ( x )= [ x ( \(x^3\) + \(x^2\) + 7x ) = 0 ]
P (x) = [ \(x^4\) + \(x^3\) + \(7x^2\) = 0 ]
Giải phương trình:
1. ( \(x^4\) = 0 ): Ta có nghiệm ( x = 0)
2. ( \(x^3\) = 0): Ta có nghiệm ( x = 0 )
3. ( \(7x^2\) = 0 ): Ta có nghiệm ( x = 0 )
=> Nghiệm là x = 0
Vậy nghiệm của đa thức P (x) là x = 0
Đặt P(x)=0
=>\(x^3+x^2+7x=0\)
=>\(x\left(x^2+x+7\right)=0\)
mà \(x^2+x+7=x^2+x+\dfrac{1}{4}+\dfrac{27}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{27}{4}>=\dfrac{27}{4}\forall x\)
nên x=0

a: ΔABC vuông cân tại A
mà AD là đường trung tuyến
nên AD\(\perp\)BC
ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
Xét ΔDAB vuông tại D có \(\widehat{DBA}=45^0\)
nên ΔDAB vuông cân tại D
Xét ΔDAC vuông tại D có \(\widehat{DCA}=45^0\)
nên ΔDAC vuông cân tại D
b: Ta có: \(\widehat{EAB}+\widehat{EAC}=90^0\)
\(\widehat{EAC}+\widehat{FCA}=90^0\)
Do đó: \(\widehat{EAB}=\widehat{FCA}\)
Xét ΔEAB vuông tại E và ΔFCA vuông tại F có
AB=CA
\(\widehat{EAB}=\widehat{FCA}\)
Do đó: ΔEAB=ΔFCA
=>EB=FA
c: Xét tứ giác AEDB có \(\widehat{AEB}=\widehat{ADB}=90^0\)
nên AEDB là tứ giác nội tiếp
=>\(\widehat{AED}+\widehat{ABD}=180^0\)
mà \(\widehat{AED}+\widehat{MED}=180^0\)(kề bù)
nên \(\widehat{MED}=\widehat{MBA}=45^0\)
Xét tứ giác ADFC có \(\widehat{ADC}=\widehat{AFC}=90^0\)
nên ADFC là tứ giác nội tiếp
=>\(\widehat{ACD}=\widehat{AFD}=45^0\)
Xét ΔDEFcó \(\widehat{DEF}=\widehat{DFE}=45^0\)
nên ΔDEF vuông cân tại D

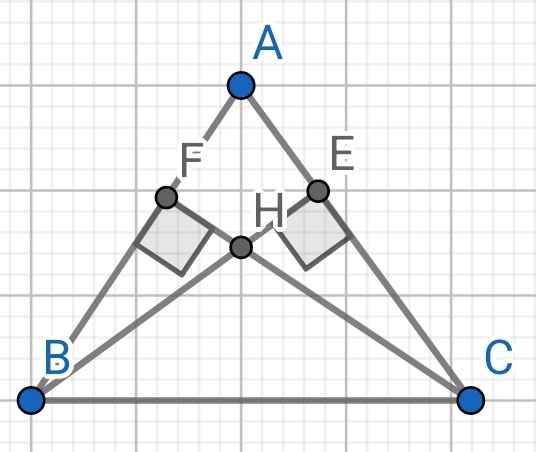
a) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB
⇒ ∠FBC = ∠ECB
Xét hai tam giác vuông: ∆BEC và ∆CFB có:
BC là cạnh chung
∠ECB = ∠FBC (cmt)
⇒ ∆BEC = ∆CFB (cạnh huyền - góc nhọn)
⇒ BE = CF (hai cạnh tương ứng)
b) Do ∆BEC = ∆CFB (cmt)
⇒ ∠EBC = ∠FCB (hai góc tương ứng)
⇒ ∠HBC = ∠HCB
∆BHC có:
∠HBC = ∠HCB (cmt)
⇒ ∆BHC cân tại H
c)
∆ABC có:
∠BAC + ∠ABC + ∠ACB = 180⁰ (tổng ba góc trong ∆ABC)
Mà ∠ABC = ∠ACB (cmt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2
= (180⁰ - 50⁰) : 2
= 65⁰

a.
\(6\left(x+11\right)-7\left(2-x\right)=26\)
\(\Leftrightarrow6x+66-14+7x=26\)
\(\Leftrightarrow6x+7x=26-66+14\)
\(\Leftrightarrow13x=-26\)
\(\Leftrightarrow x=-2\)
b.
\(\dfrac{x+23}{2021}+\dfrac{x+22}{2022}-\dfrac{x+21}{2023}-\dfrac{x+20}{2024}=0\)
\(\Leftrightarrow\dfrac{x+23}{2021}+1+\dfrac{x+22}{2022}+1-\dfrac{x+21}{2023}-1-\dfrac{x+20}{2024}-1=0\)
\(\Leftrightarrow\dfrac{x+2044}{2021}+\dfrac{x+2044}{2022}-\dfrac{x+2044}{2023}-\dfrac{x+2044}{2024}=0\)
\(\Leftrightarrow\left(x+2024\right)\left(\dfrac{1}{2021}+\dfrac{1}{2022}-\dfrac{1}{2023}-\dfrac{1}{2024}\right)=0\)
\(\Leftrightarrow x+2024=0\) (do \(\dfrac{1}{2021}+\dfrac{1}{2022}-\dfrac{1}{2023}-\dfrac{1}{2024}\ne0\))
\(\Leftrightarrow x=-2024\)
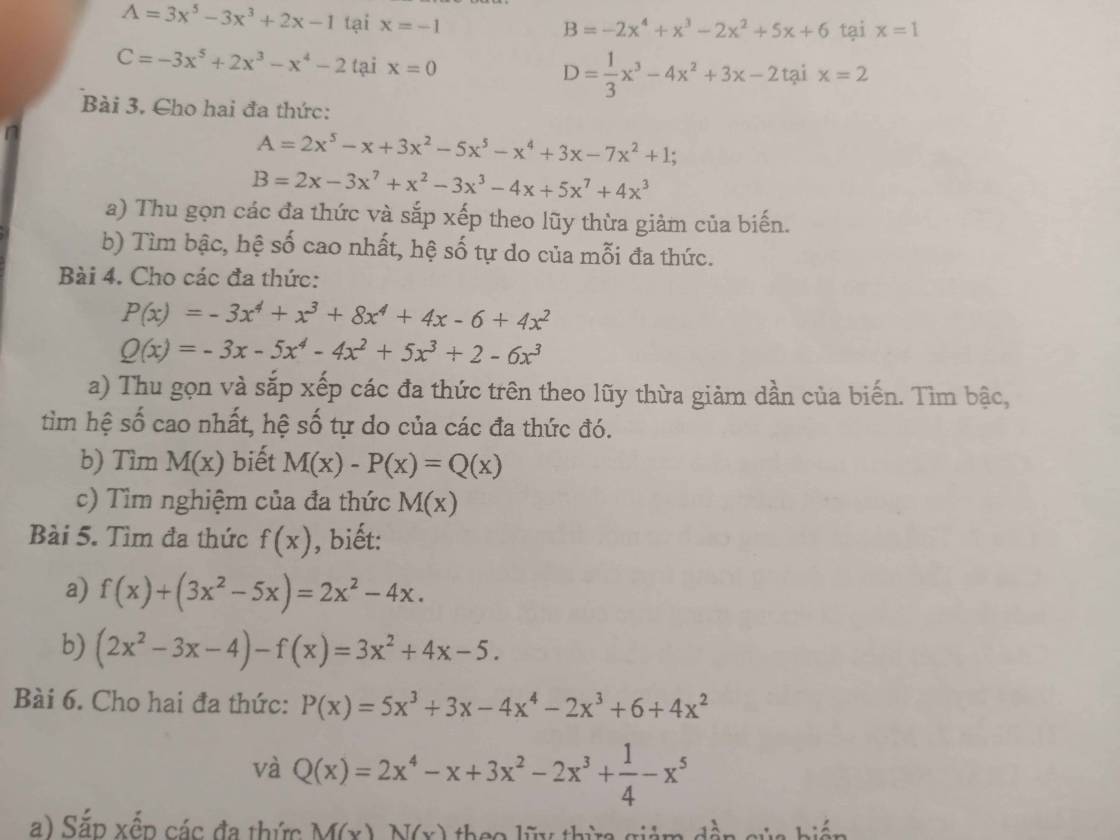

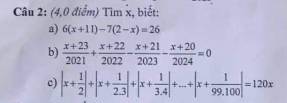
Có: \(A\left(x\right)=x^4+2x^2-x\) và \(B\left(x\right)=-x^4-\dfrac{1}{2}x^2+2x-8\)
+, \(C\left(x\right)=A\left(x\right)+B\left(x\right)\)
\(=\left(x^4+2x^2-x\right)+\left(-x^4-\dfrac{1}{2}x^2+2x-8\right)\)
\(=x^4+2x^2-x-x^4-\dfrac{1}{2}x^2+2x-8\)
\(=\dfrac{3}{2}x^2+x-8\)
+, \(D\left(x\right)=B\left(x\right)-A\left(x\right)\)
\(=\left(-x^4-\dfrac{1}{2}x^2+2x-8\right)-\left(x^4+2x^2-x\right)\)
\(=-x^4-\dfrac{1}{2}x^2+2x-8-x^4-2x^2+x\)
\(=-2x^4-\dfrac{5}{2}x^2+3x-8\)
b) Ta có: \(C\left(x\right)=\dfrac{3}{2}x^2+x-8\)
\(\Rightarrow C\left(2\right)=\dfrac{3}{2}\cdot2^2+2-8=0\)
\(\Rightarrow x=2\) là 1 nghiệm của \(C\left(x\right)\)
c) Có: \(E\left(x\right)+D\left(x\right)=2x^4\)
\(\Rightarrow E\left(x\right)=2x^4-D\left(x\right)\)
\(=2x^4-\left(-2x^4-\dfrac{5}{2}x^2+3x-8\right)\)
\(=2x^4+2x^4+\dfrac{5}{2}x^2-3x+8\)
\(=4x^4+\dfrac{5}{2}x^2-3x+8\)