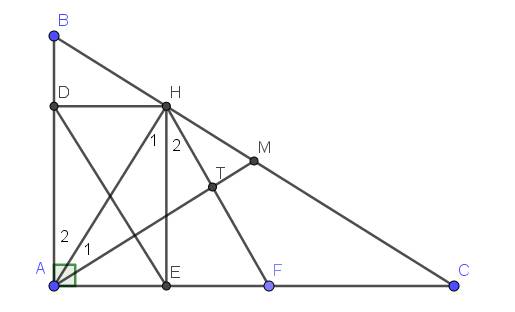
cho tam gvác abc vuông tại a trung tuyến am, đường cao ah .kẻ hd vuông góc với ab tại d ,he vuông góc ac tại e .a,chứng minh ah=de b,kẻ mf vuông góc vớv ab tại f lấy điểm k sao cho f là trung điểm của mk chứng minh tứ giác ambk la hinhf thoi và am vuông góc với de c, chứng minh bd.ac+ce.ab=ab.ac
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x+1\right)^2-3\left(x+1\right)=\left(x+1\right)\left(x+1-3\right)=\left(x+1\right)\left(x-2\right)\)
\(2x\left(x-2\right)-\left(x-2\right)^2=\left(x-2\right)\left[2x-\left(x-2\right)\right]=\left(x-2\right)\left(2x-x+2\right)=\left(x-2\right)\left(x+2\right)\)
\(4x^2-20xy+25y^2=\left(2x\right)^2-2.2x.5y+\left(5y\right)^2=\left(2x-5y\right)^2\)
\(x^2+3x-x-3=x\left(x+3\right)-\left(x+3\right)=\left(x-1\right)\left(x+3\right)\)
\(x^2-xy+x-y=x\left(x-y\right)+\left(x-y\right)=\left(x-y\right)\left(x+1\right)\)
\(2y\left(x+2\right)-3x-6=2y\left(x+2\right)-3\left(x+2\right)=\left(x+2\right)\left(2y-3\right)\)


Lời giải:
$PT \Leftrightarrow (x+1)(x-8)(x-4)(x+2)+4x^2=0$
$\Leftrightarrow (x^2-7x-8)(x^2-2x-8)+4x^2=0$
Đặt $x^2-2x-8=a$ thì:
$(a-5x)a+4x^2=0$
$\Leftrightarrow a^2-5ax+4x^2=0$
$\Leftrightarrow (a-x)(a-4x)=0$
$\Leftrightarrow a-x=0$ hoặc $a-4x=0$
Nếu $a-x=0$
$\Leftrightarrow x^2-3x-8=0\Leftrightarrow x=\frac{3\pm \sqrt{41}}{2}$
Nếu $a-4x=0$
$\Leftrightarrow x^2-6x-8=0$
$\Leftrightarrow x=3\pm \sqrt{17}$

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
=>ΔABE đồng dạng với ΔACF
=>AB/AC=AE/AF
=>AE/AB=AF/AC và AE*AC=AB*AF
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ACB
c; góc AFH=góc AEH=90 độ
=>AFHE nội tiếp (I)
=>IF=IE
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp (M)
=>MF=ME
=>MI là trung trực của EF
=>MI vuông góc EF

Ta có \(x^2+y^2+xy+x=y-1\)
\(\Leftrightarrow2x^2+2y^2+2xy+2x-2y+2=0\)
\(\Leftrightarrow\left(x+y\right)^2+\left(x+1\right)^2+\left(y-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=0\\x+1=0\\y-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
\(\Rightarrow B=\left(-1+1-1\right)^{2023}\) \(=\left(-1\right)^{2023}\) \(=-1\)

Lời giải:
a.
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$AM=\frac{BC}{2}=10:2=5$ (cm) - tính chất đường trung tuyến ứng với cạnh huyền thì bằng 1/2 cạnh huyền.
b.
Tứ giác $ADHE$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}$ nên $ADHE$ là hcn
$\Rightarrow AH=DE$.
c.
Do $AM=\frac{BC}{2}=BM$ nên tam giác $MAB$ cân tại $M$
$\Rightarrow \widehat{B}=\widehat{MAB}$
Gọi $T$ là giao điểm $HF$ và $AM$
Do $F$ đối xứng với $A$ qua $E$ nên $E$ là trung điểm của $AF$.
Tam giác $HAF$ có đường cao $HE$ đồng thời là trung tuyến nên $HAF$ cân tại $H$
$\Rightarrow HE$ cũng là đường phân giác.
$\Rightarrow \widehat{H_1}=\widehat{H_2}$
$\Rightarrow \widehat{AHT}=\widehat{H_1}+\widehat{H_2}=2\widehat{H_1}=2\widehat{A_2}=\widehat{A_2}+\widehat{A_2}$
$=\widehat{A_2}+90^0-\widehat{B}=\widehat{A_2}+90^0-\widehat{MAB}=\widehat{A_2}+90^0-(\widehat{A_1}+\widehat{A_2})$
$=90^0-\widehat{A_1}$
Vậy: $\widehat{AHT}+\widehat{A_1}=90^0$
$\Rightarrow \widehat{HTA}=180^0-(\widehat{AHT}+\widehat{A_1})=180^0-90^0=90^0$
$\Rightarrow AM\perp HF$


a, Trị giá xuất khẩu (triệu đô la Mỹ)
| Năm | 2018 | 2019 | 2020 | 2021 |
| Trị giá xuất khẩu | 3172,1 | 2879 | 2257 | 2506,6 |
b, Tổng giá trị xuất khẩu hàng hóa của ngành khai khoáng qua các năm 2018; 2019; 2020; 2021 là:
3172,1 + 2879 + 2275 + 2506,6 = 10832,7(đô)
c, So với năm 2018 thì năm 2021 giá trị xuất khẩu giảm:
3172,1 - 2506,6 = 665,5 (đô)
So với năm 2020 thì giá trị xuất khẩu năm 2021 tăng số phần trăm là:
(2506,6 - 2275):2257 x100 ≈ 10,2 %
Vậy nhận định của bài báo cáo là đúng