(x+7)^n+1-(x+7)^n-3=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x-2011|+|2025-x|\geq |x-2011+2025-x|=4$
$|x-2023|\geq 0$ với mọi $x$
$\Rightarrow P=|x-2011|+|2025-x|+|x-2023|\geq 4+0=4$
Vậy $P_{\min}=4$
Giá trị này đạt tại $(x-2011)(2025-x)\geq 0$ và $x-2023=0$
Hay $x=2023$.

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
c: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
=>\(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Gọi H là giao điểm của AB và CK
Xét ΔBHC có
BK,CA là các đường cao
BK cắt CA tại D
Do đó: D là trực tâm của ΔBHC
=>DH\(\perp\)BC
mà DE\(\perp\)BC
và DH,DE có điểm chung là D
nên H,D,E thẳng hàng
=>BA,DE,CK đồng quy

a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
=>\(\widehat{ACB}=47^0\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=180^0-2\cdot47^0=86^0\)
b: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
c Xét ΔAMB có AM+BM>AB
mà AB=AC(ΔABC cân tại A)
nên AM+BM>AC

i: Đặt x2+2x+3=0
=>\(x^2+2x+1+2=0\)
=>\(\left(x+1\right)^2+2=0\)(vô lý)
=>\(x\in\varnothing\)
k: \(3x^2+8x-11=0\)
=>\(3x^2+11x-3x-11=0\)
=>(3x+11)(x-1)=0
=>\(\left[{}\begin{matrix}x=-\dfrac{11}{3}\\x=1\end{matrix}\right.\)
m: Đặt \(x^2+8x+20=0\)
=>\(x^2+8x+16+4=0\)
=>\(\left(x+4\right)^2+4=0\)(vô lý)
=>\(x\in\varnothing\)

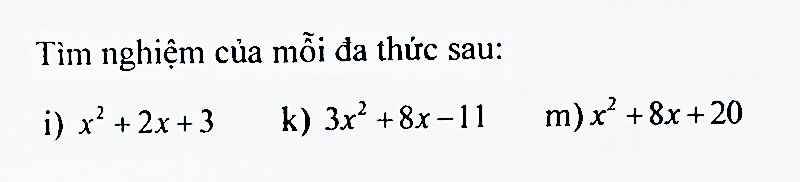
Lời giải:
$(x+7)^{n+1}-(x+7)^{n-3}=0$
$(x+7)^{n-3}[(x+7)^4-1]=0$
$\Rightarrow (x+7)^{n-3}=0$ hoặc $(x+7)^4-1=0$
Nếu $(x+7)^{n-3}=0$
$\Rightarrow x+7=0\Rightarrow x=-7$
Nếu $(x+7)^4-1=0$
$\Rightarrow (x+7)^4=1=1^4=(-1)^4$
$\Rightarrow x+7=1$ hoặc $x+7=-1$
$\Rightarrow x=-6$ hoặc $x=-8$.