B C P A H I O K x

Gọi I là giao của CP với AH; K là giao của CA với BP

\(sđ\widehat{CAx}=\dfrac{1}{2}sđcungAC\) (góc giữa tiếp tuyến và dây cung) (1)

\(sđ\widehat{BKC}=\dfrac{1}{2}\left(sđcungBC-sđcungAB\right)\) (góc có đỉnh ở ngoài hình tròn)

Ta có

\(sđcungBC=sđcungBAC\)

\(\Rightarrow sđcungBC-sđcungAB=sđcungBAC-sđcungAB=sđcungAC\)

\(\Rightarrow sđ\widehat{BKC}=\dfrac{1}{2}sđcungAC\) (2)

\(\widehat{CAx}=\widehat{KAP}\) (góc đối đỉnh) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{KAP}=\widehat{BKC}\) => tg APK cân tại P

=> PA=PK

Mà PA=PB (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)

=> PK=PB

Ta có

\(BK\perp BC;AH\perp BC\) => AH//BK

Xét tg BCK có

\(\dfrac{IA}{PK}=\dfrac{IH}{PB}\) mà PK=PB (cmt) => IA=IH => I là trung điểm của AH

Số tự nhiên 2 chữ số  \(\overline{xy}=10x+y\)

Hai lần chữ số hàng chục hơn chữ số hàng đơn vị : \(2x-y=1\left(1\right)\)

Khi viết ngược lại :

\(10y+x-\left(10x+y\right)=27\)

\(\Rightarrow10y+x-10x-y=27\)

\(\Rightarrow-9x+9y=27\left(2\right)\)

\(\left(1\right),\left(2\right)\) ta có hệ phương trình

\(\left\{{}\begin{matrix}2x-y=1\\-9x+9y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}18x-9y=9\\-18x+18y=54\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}9y=63\\2x-y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=7\\x=\dfrac{y+1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=7\end{matrix}\right.\)

Vậy số tự nhiên đó là 47

 Ta nhận thấy \(AH^2=\left(2\sqrt{5}\right)^2=20\) và \(BH.CH=4.5=20\) và \(AH\perp BC\) tại H nên tam giác ABC sẽ là tam giác vuông tại A. chỉ cần làm như sau:

 Vẽ đường thẳng d bất kì. Trên đó lấy 3 điểm B, C, H sao cho H nằm giữa B và C thỏa mãn \(BH=4cm,CH=5cm\)

Sau đó, ta chỉ cần dựng đường thẳng qua H vuông góc với BC cắt đường tròn đường kính BC tại A là xong.

Sau đó ta xóa đi các chi tiết thừa và được hình vẽ đúng theo ycbt.

Lê Song Phương, em ơi, em vẽ hình đẹp quá, thế điểm I; K đối xứng với H qua AB và AC của cô đâu rồi nhỉ? 

Bài này chỉ cần vẽ hình,nhưng cô tìm mãi vẫn chưa thấy I và K đâu em ha!

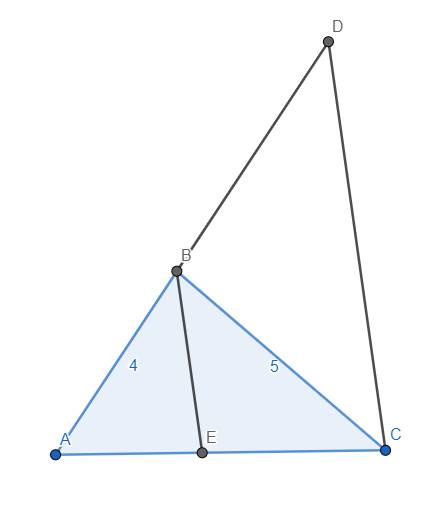
a) Xét tam giác ACB và ADC, có \(\widehat{A}\) chung và \(\widehat{ACB}=\widehat{ADC}\left(gt\right)\), suy ra đpcm.

b) Từ câu a) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AC}{AD}\) \(\Rightarrow AC^2=AB.AD\)

Kẻ phân giác BE của tam giác ABC. Vì \(\widehat{B}=2\widehat{C}\)  nên \(\widehat{ABE}=\widehat{ADC}\) hay BE//CD. Mặt khác, \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{4}{5}\) nên suy ra \(\dfrac{BA}{BD}=\dfrac{4}{5}\Leftrightarrow\dfrac{4}{BD}=\dfrac{4}{5}\Leftrightarrow BD=5\),  suy ra \(AD=AB+BD=4+5=9\).

\(\Rightarrow AC^2=AB.AD=4.9=36\) \(\Rightarrow AC=6\).

Vậy \(AC=6\)

 Dạ thưa cô, cái này em áp dụng tính chất đường phân giác trong tam giác ạ. Cái này lớp 9 được dùng luôn không cần chứng minh ạ.

đoán xem

Đặt y = 0, ta có:
-5x - 1 = 0

Giải phương trình trên, ta có:
-5x = 1
x = -1/5

Vậy, đồ thị hàm số y = -5x - 1 đi qua điểm (-1/5, 0).