giúp em tip với ạ=))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2:
a: \(x-\dfrac{1}{3}=\dfrac{5}{2}\)
=>\(x=\dfrac{5}{2}+\dfrac{1}{3}=\dfrac{15}{6}+\dfrac{2}{6}=\dfrac{17}{6}\)
b: \(\left(1-2x\right)^2=\dfrac{4}{9}\)
=>\(\left(2x-1\right)^2=\dfrac{4}{9}\)
=>\(\left[{}\begin{matrix}2x-1=\dfrac{2}{3}\\2x-1=-\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{5}{3}\\2x=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{6}\\x=\dfrac{1}{6}\end{matrix}\right.\)
Câu 1:
a: \(-\dfrac{4}{3}+\dfrac{3}{2}:\dfrac{9}{4}\)
\(=\dfrac{-4}{3}+\dfrac{3}{2}\cdot\dfrac{4}{9}\)
\(=\dfrac{-4}{3}+\dfrac{2}{3}=-\dfrac{2}{3}\)
b: \(\left(\dfrac{10}{9}+\dfrac{13}{7}\right)-\left(\dfrac{19}{9}-\dfrac{1}{7}\right)\)
\(=\dfrac{10}{9}+\dfrac{13}{7}-\dfrac{19}{9}+\dfrac{1}{7}=\left(\dfrac{10}{9}-\dfrac{19}{9}\right)+\left(\dfrac{13}{7}+\dfrac{1}{7}\right)\)
=-1+2
=1

1/5 giờ=12 phút
\(1\dfrac{1}{3}phút=80\left(giây\right)\)
7m45cm=745cm

\(-\dfrac{4}{3}+\dfrac{3}{2}:\dfrac{27}{12}=\dfrac{-4}{3}+\dfrac{3}{2}\cdot\dfrac{12}{27}\)
\(=\dfrac{-4}{3}+\dfrac{3}{2}\cdot\dfrac{4}{9}=\dfrac{-4}{3}+\dfrac{2}{3}=-\dfrac{2}{3}\)

a: Vì \(32⋮4\)
nên \(32\cdot27\cdot14⋮4\)
=>\(A⋮4\)
b: \(20⋮4\)
=>\(20\cdot43\cdot41⋮4\)
=>\(B⋮4\)
c: \(124⋮4\)
=>\(124\cdot45\cdot29⋮4\)
=>\(C⋮4\)
d: \(22\cdot2=44⋮4\)
=>\(22\cdot127\cdot2\cdot15⋮4\)
=>\(D⋮4\)
a) A = 32 . 27 . 14
= 4 . 8 . 27 . 14 chia hết cho 4
b) B = 20 . 43 . 41
= 4 . 5 . 43 . 41 chia hết cho 4
c) C = 124 . 45 . 29
= 4 . 31 . 45 . 29 chia hết cho 4
d) D = 22 . 127 . 2 . 15
= 2 . 11 . 127 . 2 . 15
= ( 2 . 2 ) . 11 . 127 . 15
= 4 . 11 . 127 . 15 chia hết cho 4
Vậy tất cả các tích trên đều chia hết cho 4

Bạn hỏi rõ hơn được không ?
Nếu như vậy thì sẽ có số 8 nằm ngang số có đúng một chữ số 7
Có bao nhiêu chữ số có đúng một chữ số thì chỉ có 1 chữ số thôi em nhé.
Trong toán học có 10 chữ số và chỉ có duy nhất 1 chữ số 7 thôi em.

`#3107.101107`
Mình có tham khảo cách làm nha.
`2016^{2017}` và `2017^{2016}`
Ta có:
$2016^{2017} = 2016^{2,017 \cdot 1000} = (2016^{2,017})^{1000}$
$2017^{2016} = 2017^{2,016 \cdot 1000} = (2017^{2,016})^{1000}$
Vì `2016^{2,017} > 2017^{2,016}`
`\Rightarrow (2016^{2,017})^{1000} > (2017^{2,016})^{1000}`
`\Rightarrow 2016^{2017} > 2017^{2016}.`

Để xác định số nguyên lớn nhất không vượt quá số A = 2020^2021 + (2021^2022 / 2020^2020 + 2021^2021), chúng ta cần thực hiện các bước sau:
-
Tính giá trị của A:
- 2020^2021 = 2,8 × 10^2728
- 2021^2022 = 2,1 × 10^2833
- 2020^2020 = 2,6 × 10^2728
- 2021^2021 = 1,6 × 10^2833
- A = 2,8 × 10^2728 + (2,1 × 10^2833 / 2,6 × 10^2728 + 1,6 × 10^2833)
- A ≈ 2,8 × 10^2728 + 1,3 × 10^105 ≈ 2,8 × 10^2728
-
Tìm số nguyên lớn nhất không vượt quá A:
- Số nguyên lớn nhất không vượt quá 2,8 × 10^2728 là 2,8 × 10^2728 - 1 = 2,799999999999999... × 10^2728
Vì vậy, số nguyên lớn nhất không vượt quá số A = 2020^2021 + (2021^2022 / 2020^2020 + 2021^2021) là 2,799999999999999... × 10^2728.

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.
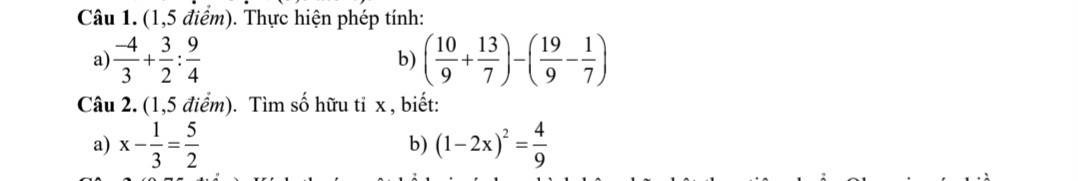
Bài 2:
a: \(\dfrac{5}{2}-x=\dfrac{27}{8}\)
=>\(x=\dfrac{5}{2}-\dfrac{27}{8}=\dfrac{20}{8}-\dfrac{27}{8}=-\dfrac{7}{8}\)
b: \(-\dfrac{1}{3}+\dfrac{4}{10}x=0,2\)
=>\(\dfrac{2}{5}x=0,2+\dfrac{1}{3}=\dfrac{1}{5}+\dfrac{1}{3}=\dfrac{8}{15}\)
=>\(x=\dfrac{8}{15}:\dfrac{2}{5}=\dfrac{8}{15}\cdot\dfrac{5}{2}=\dfrac{40}{30}=\dfrac{4}{3}\)
c: \(\left(3x+2\right)^2=\dfrac{25}{49}\)
=>\(\left[{}\begin{matrix}3x+2=\dfrac{5}{7}\\3x+2=-\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{5}{7}-2=-\dfrac{9}{7}\\3x=-\dfrac{5}{7}-2=-\dfrac{19}{7}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{3}{7}\\x=-\dfrac{19}{21}\end{matrix}\right.\)
Bài 1:
a: \(\dfrac{5}{6}+\dfrac{-11}{30}+\dfrac{7}{5}\)
\(=\dfrac{25}{30}-\dfrac{11}{30}+\dfrac{42}{30}=\dfrac{56}{30}=\dfrac{28}{15}\)
b: \(\left(-\dfrac{4}{5}\right)^2\cdot\dfrac{57}{2}+\dfrac{-7}{2}\cdot\left(-\dfrac{4}{5}\right)^2\)
\(=\left(-\dfrac{4}{5}\right)^2\left(\dfrac{57}{2}-\dfrac{7}{2}\right)=\dfrac{16}{25}\cdot25=16\)
c: \(\left(\dfrac{7}{25}-1\dfrac{2}{9}\right)-\left(\dfrac{23}{54}-\dfrac{18}{25}\right)+\dfrac{-31}{54}\)
\(=\dfrac{7}{25}-\dfrac{11}{9}-\dfrac{23}{54}+\dfrac{18}{25}-\dfrac{31}{54}\)
\(=\left(\dfrac{7}{25}+\dfrac{18}{25}\right)-\left(\dfrac{23}{54}+\dfrac{31}{54}\right)-\dfrac{11}{9}=1-1-\dfrac{11}{9}=-\dfrac{11}{9}\)