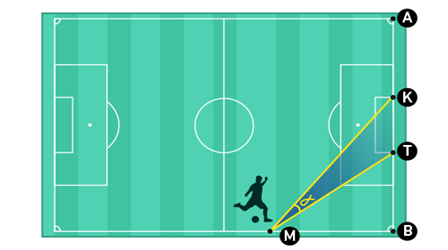
Cho tam giác đều \(ABC\) có độ dài cạnh bằng \(a\). Gọi \(M\) là 1 điểm nằm trong tam giác. \(MI,MP,MQ\) theo thứ tự là khoảng cách từ \(M\) đến các cạnh \(BC,AB,AC\). Gọi \(O\) là trung điểm của cạnh \(BC\). Các điểm \(D\) và \(E\) theo thứ tự chuyển động trên các cạnh \(AB\) và \(AC\) sao cho \(\widehat{DOE}=60^o\).
\(a\)) Chứng minh: \(MI+MP+MQ\) không đổi.
\(b\)) Chứng minh: Đường thẳng \(DE\) luôn tiếp xúc với một đường tròn cố định.
\(c\)) Xác định vị trí của \(D\) và \(E\) để diện tích tam giác \(DOE\) đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo \(a\).

Bài 3 (3 điểm)

1) Cho đường tròn $(O)$ và một điểm $P$ nằm ngoài đường tròn $(O)$. Từ $P$ vẽ hai tiếp tuyến $PA$, $PB$ của đường tròn $(O)$ ($A$ và $B$ là hai tiếp điểm tiếp điểm). Gọi $H$ là giao điểm của $OP$ và $AB$.

a) Chứng minh $OP$ vuông góc với $AB$ tại $H$.

b) Từ $A$ vẽ đường kính $AD$ của $(O)$, đường thẳng $PD$ cắt $(O)$ tại $E$ (khác $D$). Chứng minh: $PD.PE = PH.PO$.

2) Chiều rộng của sân bóng đá và của khung thành là $AB = 64,32$ m, $KT = 7,32$ m và $AK = TB$.

Một cầu thủ điều khiển bóng tấn công dọc theo đường biên và sút bóng tại vị trí $M$ cách $B$ một khoảng $35$ m. Tính góc sút $\alpha $ khi bóng đi trúng khung thành $KT$ (làm tròn đến độ).

Câu 6. (3,0 điểm) Từ một điểm ${{A}}$ nằm ngoài đường tròn ${{(O ; R)}}$, kẻ hai tiếp tuyến ${{AB, A C}}$ với $(O;R)\,\,\,(B$ và ${{C}}$ là hai tiếp điểm).

a) Chứng minh bốn điểm $A, \, B, \, O, \, C$ cùng thuộc một đường tròn và $A O \perp B C$ tại ${{H}}$.

b) Vẽ đường kính ${{B D}}$. Đường thẳng qua ${{O}}$ và vuông góc với ${{A D}}$ cắt tia ${{B C}}$ tại ${{E}}$. Chứng minh $D C$ // $O A$ và ${{C D \cdot C O=A B \cdot C E}}$.

c) Chứng minh ${{D E}}$ là tiếp tuyến của đường tròn ${{(O ; R)}}$.