Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Olm chào em, đây là dạng toán nâng cao giải phương trình nghiệm nguyên. cấu trúc thi chuyên. Hôm nay olm.vn sẽ hướng dẫn em giải dạng này bằng phương pháp chặn kết hợp với lập bảng chi tiết như sau:
Bước 1: Chặn để giới hạn nghiệm cần tìm trong một khoảng nào đó.
Bước 2: Kết hợp với điều kiện lập bảng tìm nghiệm nguyên
Bước 3 kết luận:
Giải:
\(x^2\) + y2 + 2\(x\) = 17
\(x^2\) + y2 + 2\(x\) + 1 = 17 + 1
(\(x^2\) + 2\(x\) + 1) + y2 = 18
(\(x\) + 1)2 + y2 = 18
Vì y2 ≥ 0 ∀ y nên 0 ≤ y2 ≤ 18
Vì y \(\in\) Z nên y2 \(\in\) {0; 1; 4; 9; 16; 25; ...;}
Vì 0 ≤ y2 ≤ 18 nên y2 \(\in\) {0; 1; 4; 9; 16}
Lập bảng ta có:
| y2 | 0 | 1 | 4 | 9 | 16 |
| (\(x+1\))2 = 18 - y2 | 18 | 17 | 14 | 9 | 2 |
| \(y\) \(\in\) Z | -3; 3 | ||||
| \(x\) + 1 | loại | (loại) | loại | -3; 3 | loại |
| \(x\in\) Z | -4; 2 |
Theo bảng trên ta có các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) = (-4; -3); (-4; 3); (2; -3); (2; 3)
Vậy (\(x;y\)) = (-4; -3); (-4; 3); (2; -3); (2; 3) là nghiệm nguyên của phương trình.

A B C D E F I M
b/
\(C_{MCE}=MC+ME+CE\)
Mà ME=MF (cmt)
\(\Rightarrow C_{MCE}=MC+MF+CE=MC+MD+DF+CE=\)
\(=CD+DF+CE\) Mà DF=BE (gt)
\(\Rightarrow C_{MCE}=CD++BE+CE=CD+BC=2.BC\) không đổi

a: Ta có; ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25=5^2\)
=>BC=5
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{DC}=\dfrac{BA}{BC}=\dfrac{3}{5}\)(1)
b: Ta có: AH\(\perp\)BC
DE\(\perp\)BC
Do đó: AH//DE
Xét ΔCAH có DE//AH
nên \(\dfrac{HE}{EC}=\dfrac{AD}{DC}\)(2)
Từ (1),(2) suy ra \(\dfrac{HE}{EC}=\dfrac{BA}{BC}\)

a: Xét ΔABC có
M,N lần lượt là trung điểm của BA,BC
=>MN là đường trung bình của ΔABC
=>MN//AC và \(MN=\dfrac{AC}{2}\)
=>\(AC=2\cdot MN=2\cdot7=14\left(cm\right)\)
b: Xét ΔCAB có
Y,N lần lượt là trung điểm của CA,CB
=>YN là đường trung bình của ΔCAB
=>YN//AB và YN=AB/2
Ta có: YN//AB
M\(\in\)AB
Do đó: YN//MB
Ta có: \(YN=\dfrac{AB}{2}\)
\(MB=\dfrac{AB}{2}\)
Do đó: YN=MB
Xét tứ giác YNBM có
YN//MB
YN=MB
Do đó: YNBM là hình bình hành
=>YB cắt NM tại trung điểm của mỗi đường
=>K là trung điểm của MN

Sửa đề: ΔABC vuông tại A
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB^2=10^2-8^2=36=6^2\)
=>AB=6(cm)
Xét ΔABC có CD là phân giác
nên \(\dfrac{AD}{AC}=\dfrac{BD}{CB}\)
=>\(\dfrac{AD}{8}=\dfrac{BD}{10}\)
=>\(\dfrac{AD}{4}=\dfrac{BD}{5}\)
mà AD+BD=AB=6cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{4}=\dfrac{BD}{5}=\dfrac{AD+BD}{4+5}=\dfrac{6}{9}=\dfrac{2}{3}\)
=>\(AD=\dfrac{2}{3}\cdot4=\dfrac{8}{3}\left(cm\right);BD=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)

Lời giải:
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
Tiếp tục áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)



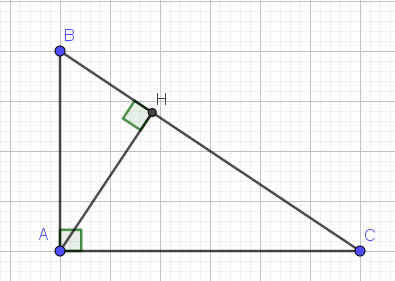
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔABD~ΔACE
b: Xét ΔOEB vuông tại E và ΔODC vuông tại D có
\(\widehat{EOB}=\widehat{DOC}\)(hai góc đối đỉnh)
Do đó: ΔOEB~ΔODC
=>\(\dfrac{OE}{OD}=\dfrac{OB}{OC}\)
=>\(OE\cdot OC=OD\cdot OB\)