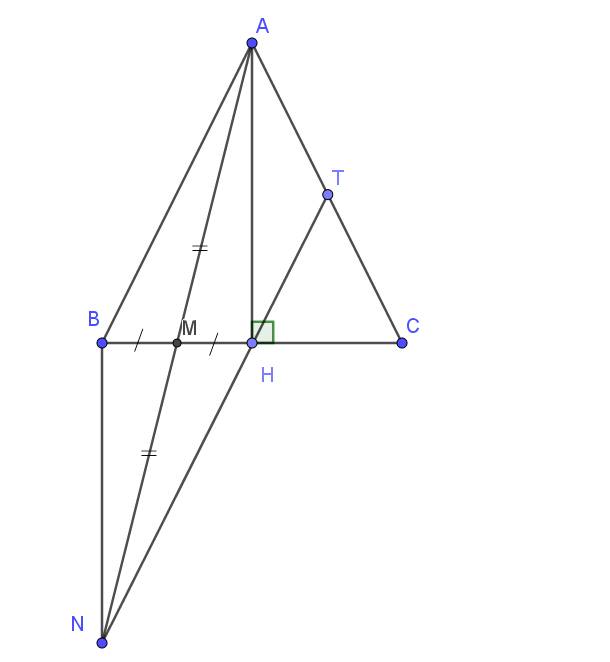
a: ΔABC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-\widehat{A}}{2}=\dfrac{180^0-50^0}{2}=65^0\)

b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

c: ΔAHB=ΔAHC

=>HB=HC

=>H là trung điểm của BC

Xét ΔABC có

AH,BD là các đường trung tuyến

AH cắt BD tại G

Do đó: G là trọng tâm của ΔABC

=>\(GH=\dfrac{GA}{2}\)

d: Xét ΔABC có

H là trung điểm của BC

HE//AC

Do đó: E là trung điểm của AB

Xét ΔABC có

G là trọng tâm

E là trung điểm của AB

Do đó: C,G,E thẳng hàng

Trong các số đo chiều cao của tầng hầm không có chiều cao nào lớn hơn 25 m.

\(\dfrac{-2}{7}>\dfrac{-3}{4}\)

A.47

Lấy 38+9=47

\(\dfrac{1}{-5}>\dfrac{-3}{5}\)

\(\dfrac{1}{-5}=\dfrac{-1}{5}\)

\(=>\dfrac{-1}{5}>\dfrac{-3}{5}\)

ab chia 5 dư \(1.2=2\)

\(\dfrac{4}{-7}=\dfrac{-4}{7};\dfrac{3}{-7}=\dfrac{-3}{7}\)

\(=>\dfrac{-4}{7}< \dfrac{-3}{7}\)

\(\dfrac{4}{-7}\)<\(\dfrac{3}{-7}\)

Các phân số biểu thị: \(-\dfrac{8}{18},-\dfrac{12}{27};-\dfrac{4}{9}.\)

Các phân số cùng biểu diễn \(\dfrac{4}{-9}\) là: \(\dfrac{-8}{18};\dfrac{-12}{27};\dfrac{-4}{9}\)

Lời giải:
a.

Xét tam giác $ABH$ và $ACH$ có:

$AH$ chung

$\widehat{AHB}=\widehat{AHC}=90^0$

$AB=AC$ (do $ABC$ cân tại $A$)

$\Rightarrow \triangle ABH=\triangle ACH$ (ch-cgv)

b.

Xét tam giác $AHM$ và $NBM$ có:

$AM=NM$

$HM=BM$
$\widehat{AMH}=\widehat{NMB}$ (đối đỉnh)

$\Rightarrow \triangle AHM=\triangle NBM$ (c.g.c)

$\Rightarrow \widehat{NBM}=\widehat{AHM}=90^0$

$\Rightarrow NB\perp BM$ hay $NB\perp BC$

c.

Từ tam giác bằng nhau phần b suy ra $BN=AH$. Mà $AH< AB$ (trong tam giác vuông cạnh huyền là lớn nhất)

$\Rightarrow BN< AB$

$\Rightarrow \widehat{BAN}< \widehat{BNA}$

d.

Gọi $T$ là giao điểm của $NH$ và $AC$

Dễ thấy $\triangle BAM=\triangle HNM$ (c.g.c)

$\Rightarrow \widehat{BAM}=\widehat{HNM}$

Mà 2 góc này ở vị trí so le trong nên $HN\parallel AB$

Hay $NT\parallel AB$

$\Rightarrow \widehat{BAH}=\widehat{H_1}$

Mà $\widehat{BAH}=\widehat{A_2}$ (do $\triangle ABH=\triangle ACH$)

$\Rightarrow \widehat{H_1}=\widehat{A_2}$

$\Rightarrow \triangle ATH$ cân tại $T$

$\Rightarrow AT=TH(1)$

Lại có:

$\widehat{H_1}=\widehat{A_2}$
$\Rightarrow 90^0-\widehat{H_1}=90^0-\widehat{A_2}$

$\Rightarrow \widehat{H_2}=\widehat{C_1}$

$\Rightarrow THC$ cân tại $T$

$\Rightarrow TH=TC(2)$

Từ $(1); (2)\Rightarrow AT=TC\Rightarrow T$ là trung điểm $AC$
$\Rightarrow T\equiv K$

$\Rightarrow N,H,K$ thẳng hàng.

Hình vẽ: