 giúp tớ bài 9 với
giúp tớ bài 9 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đây là toán nâng cao của nâng cao chuyên đề dãy số cách đều, cấu trúc
Giải:
Cứ 3 lon bia đổi được 1 lon bia nên số lon bia mất đi sau mỗi lần đổi là:
3 - 1 = 2 (lon bia)
Sau lần đổi thứ nhất số lon bia còn lại là: 30 - 2 = 28 (lon)
Sau lần đổi cuối cùng số lon bia còn lại là 2 lon (vì 2 < 3 nên không thể đổi được nữa)
Số lần đổi vỏ lon bia là: (28 - 2) : 2 + 1 = 14 (lần)
Vậy tổng số lon bia mà ngườ đó có thể uống được khi mua 30 lon bia và được tặng là:
3 x 14 + 2 = 44 (lon bia)
Đáp số: 44 lon bia

a: ΔABC có BH\(\perp\)AC
nên \(S_{ABC}=\dfrac{1}{2}\cdot BH\cdot AC\)
ΔACB có CK\(\perp\)AB
nên \(S_{ABC}=\dfrac{1}{2}\cdot CK\cdot AB\)
b: \(S_{ABC}=\dfrac{1}{2}\cdot CK\cdot AB\)
\(S_{ABC}=\dfrac{1}{2}\cdot BH\cdot AC\)
Do đó: \(CK\cdot AB=BH\cdot AC\)
mà AB=AC
nên BH/CK=1
c: Vì BH/CK=1
nên BH=CK

\(A\left(1\right)=a\cdot1^2+b\cdot1+c=a+b+c\)
\(A\left(-3\right)=a\cdot\left(-3\right)^2+b\cdot\left(-3\right)+c=9a-3b+c\)
Ta có:
\(A\left(1\right)+A\left(-3\right)=\left(a+b+c\right)+\left(9a-3b+c\right)\\ =10a-2b+2b\\ =2\left(5a+c\right)-2b\\ =2b-2b=0\\ =>A\left(1\right)+A\left(-3\right)=0=>A\left(1\right)=-A\left(-3\right)\)
Ta có:\(A\left(1\right)\cdot A\left(-3\right)=A\left(-1\right)\cdot\left[-A\left(-1\right)\right]=-\left[A\left(-1\right)\right]^2\le0\)
A(1)=a⋅12+b⋅1+c=a+b+c
�(−3)=�⋅(−3)2+�⋅(−3)+�=9�−3�+�A(−3)=a⋅(−3)2+b⋅(−3)+c=9a−3b+c
Ta có:
�(1)+�(−3)=(�+�+�)+(9�−3�+�)=10�−2�+2�=2(5�+�)−2�=2�−2�=0=>�(1)+�(−3)=0=>�(1)=−�(−3)A(1)+A(−3)=(a+b+c)+(9a−3b+c)=10a−2b+2b=2(5a+c)−2b=2b−2b=0=>A(1)+A(−3)=0=>A(1)=−A(−3)
Ta có:�(1)⋅�(−3)=�(−1)⋅[−�(−1)]=−[�(−1)]2≤0A(1)⋅A(−3)=A(−1)⋅[−A(−1)]=−[A(−1)]2≤0

Cái đó thì còn phải trông chờ vào điểm tổng kết các môn khác nữa nhé!

a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
b: ΔABD=ΔACD
=>DB=DC
=>D nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AD là đường trung trực của BC
=>AD\(\perp\)BC tại I và I là trung điểm của BC
c: Xét ΔIMB vuông tại I và ΔIDC vuông tại I có
IM=ID
IB=IC
Do đó: ΔIMB=ΔIDC
=>\(\widehat{IMB}=\widehat{IDC}\)
=>MB//DC
mà DC\(\perp\)AC
nên BM\(\perp\)AC

Lời giải:
ĐK: $-3\leq x\leq 3$
$B=\frac{3}{4}-\frac{1}{4}\sqrt{9-x^2}$
Ta thấy: $\sqrt{9-x^2}\geq 0$ với mọi $x\in$ ĐKXĐ
$\Rightarrow B\leq \frac{3}{4}-\frac{1}{4}.0=\frac{3}{4}$
Vậy $B_{\max}=\frac{3}{4}$. Giá trị này đạt tại $9-x^2=0\Leftrightarrow x=\pm 3$
---------------
Lại có:
$x^2\geq 0$ với mọi $x\in$ ĐKXĐ
$\Rightarrow 9-x^2\leq 9$
$\Rightarrow \sqrt{9-x^2}\leq 3$
$\Rightarrow B\geq \frac{3}{4}-\frac{1}{4}.3=0$
Vậy $B_{\min}=0$. Giá trị này đạt tại $x=0$

ĐKXĐ: \(\left[{}\begin{matrix}x>=2\\x< =-2\end{matrix}\right.\)
\(\dfrac{1}{4}\sqrt{x^2-4}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{1}{4}\sqrt{x^2-4}< =0\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{1}{4}\sqrt{x^2-4}+1< =1\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(x^2-4=0\)
=>\(x^2=4\)
=>\(\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

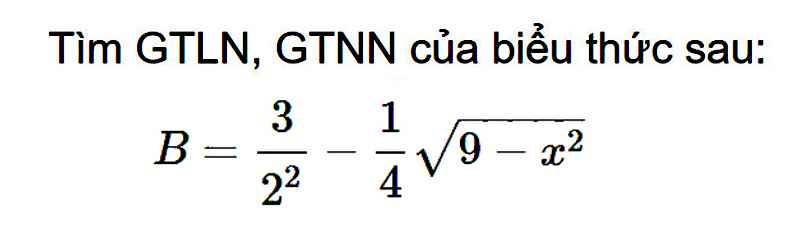
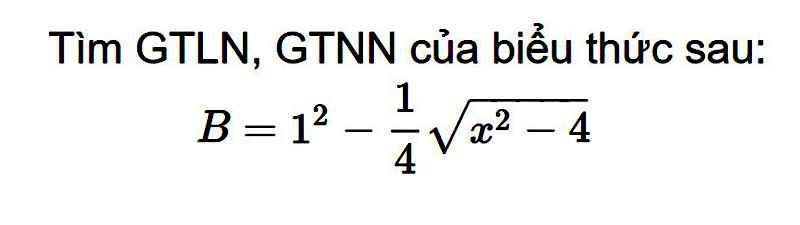
Bài 9:
\(A=A_1A_2A_3...A_{100}=(\frac{1}{2}x)(\frac{2}{3}x^2)(\frac{3}{4}x^3)...(\frac{100}{101}x^{100})\)
\(=(\frac{1}{2}.\frac{2}{3}.\frac{3}{4}....\frac{100}{101})(x.x^2.x^3...x^{100})\\ =\frac{1.2.3...100}{2.3.4...100.101}.x^{1+2+3+...+100}\\ =\frac{1}{101}.x^{100.101:2}=\frac{x^{5050}}{101}\)