
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(\dfrac{8^{10}}{4^8}=\dfrac{\left(2^3\right)^{10}}{\left(2^2\right)^8}=\dfrac{2^{30}}{2^{16}}=2^{30-16}=3^{14}\)
2) \(\dfrac{4^2\cdot4^3}{2^{10}}=\dfrac{4^{2+3}}{\left(2^2\right)^5}=\dfrac{4^5}{4^5}=1\)
3) \(\dfrac{8^2\cdot4^5}{2^{20}}=\dfrac{\left(2^3\right)^2\cdot\left(2^2\right)^5}{2^{20}}=\dfrac{2^6\cdot2^{10}}{2^{20}}=\dfrac{2^{16}}{2^{20}}=\dfrac{1}{2^4}=\dfrac{1}{16}\)
4) \(\dfrac{2^7\cdot9^3}{6^5\cdot8^2}=\dfrac{2^7\cdot\left(3^2\right)^3}{2^5\cdot3^5\cdot\left(2^3\right)^2}=\dfrac{2^7\cdot3^6}{2^5\cdot3^5\cdot2^6}=\dfrac{2^7\cdot3}{2^{11}}=\dfrac{3}{2^4}=\dfrac{3}{16}\)
5) \(\dfrac{2^{15}\cdot9^4}{6^6\cdot8^3}=\dfrac{2^{15}\cdot\left(3^2\right)^4}{3^6\cdot2^6\cdot\left(2^3\right)^3}=\dfrac{2^{15}\cdot3^8}{3^6\cdot2^6\cdot2^9}=\dfrac{2^{15}\cdot3^2}{2^{15}}=3^2=9\)
6) \(\dfrac{2^7\cdot9^3}{6^3\cdot8^2}=\dfrac{2^7\cdot\left(3^2\right)^3}{2^3\cdot3^3\cdot\left(2^3\right)^2}=\dfrac{2^7\cdot3^6}{2^3\cdot3^3\cdot2^6}=\dfrac{2^7\cdot3^3}{2^9}=\dfrac{3^3}{2^2}=\dfrac{27}{4}\)

\(1,\left(1\right)\cdot x=1\)
\(\Rightarrow x=\dfrac{1}{1,\left(1\right)}\)
\(\Rightarrow x=1:\dfrac{10}{9}\)
\(\Rightarrow x=\dfrac{9}{10}=0,9\)
Vậy số thập phân x thỏa mãn là 0,9
\(1,\left(1\right).x=1\)
\(\left(1+\dfrac{1}{9}\right).x=1\)
\(\dfrac{10}{9}.x=1\)
\(x=1:\dfrac{10}{9}\)
\(x=\dfrac{9}{10}\)
\(x=0,9\)

\(-\dfrac{1}{1\times4}-\dfrac{1}{4\times7}-\dfrac{1}{7\times10}-\dfrac{1}{10\times13}\)
\(=-\left(\dfrac{1}{1\times4}+\dfrac{1}{4\times7}+\dfrac{1}{7\times10}+\dfrac{1}{10\times13}\right)\)
\(=-\dfrac{1}{3}\cdot\left(\dfrac{3}{1\times4}+\dfrac{3}{4\times7}+\dfrac{3}{7\times10}+\dfrac{3}{10\times13}\right)\)
\(=-\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}\right)\)
\(=-\dfrac{1}{3}\cdot\left(1-\dfrac{1}{13}\right)\)
\(=\dfrac{-1}{3}\cdot\dfrac{12}{13}\)
\(=\dfrac{-4}{13}\)

Ta có:
2024 ≡ 2024 (mod 2025)
2024² ≡ 1 (mod 2025)
2024³ ≡ 2024.2024² (mod 2025) ≡ 2024.1 (mod 2025) ≡ 2024 (mod 2025)
2024⁴ ≡ (2024²)² (mod 2025) ≡ 1² (mod 2025) ≡ 1 (mod 2025)
⇒ 2024 + 2024² + 2024³ + 2024⁴ ≡ 2024 + 1 + 2024 + 1 (mod 2025) 4050 ≡ (mod 2025) ≡ 0 (mod 2025)
Vậy (2024 + 2024² + 2024³ + 2024⁴) ⋮ 2025
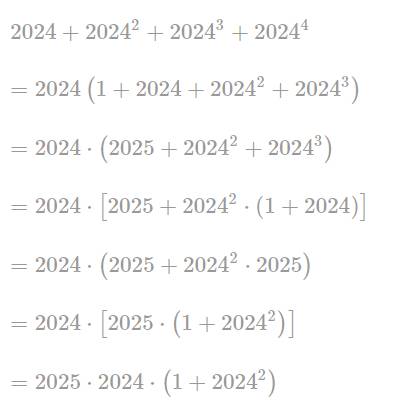
\(\Rightarrow2025\cdot2024\cdot\left(1+2024^2\right)\) ⋮ 2025
\(\Rightarrow\left(2024+2024^2+2024^3+2024^4\right)⋮2025\)

3x=4y=5z
=>\(\dfrac{3x}{60}=\dfrac{4y}{60}=\dfrac{5z}{60}\)
=>\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{12}\)
mà x-y-z=-21
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{12}=\dfrac{x-y-z}{20-15-12}=\dfrac{-21}{-7}=3\)
=>\(x=3\cdot20=60;y=15\cdot3=45;z=12\cdot3=36\)

\(a,M\left(x\right)=A\left(x\right)-2\cdot B\left(x\right)+C\left(x\right)\\ =\left(2x^5-4x^3+x^2-2x+2\right)-2\left(x^5-2x^4+x^2-5x+2\right)+\left(x^4+4x^3+3x^2-8x+2\dfrac{3}{4}\right)\\ =2x^5-4x^3+x^2-2x+2-2x^5+4x^4-2x^2+10x-4+x^4+4x^3+3x^2-8x+2,75\\ =\left(2x^5-2x^5\right)+\left(4x^4+x^4\right)+\left(-4x^3+4x^3\right)+\left(x^2-2x^2+3x^2\right)+\left(-2x+10x-8x\right)+\left(2-4+2,75\right)\\ =5x^4+2x^2+0,75\)
b, Thay x = -√0,25 = -0,5 vào M(x)
\(M\left(-0,5\right)=5\cdot\left(-0,5\right)^4+2\cdot\left(-0,5\right)^2+0,75\\ =0,3125+0,5+0,75\\ =1,5625\)
c, Vì \(5x^4\ge0;2x^2\ge0=>M\left(x\right)\ge0,75\)
Vậy không có giá trị nào của x để M(x) = 0


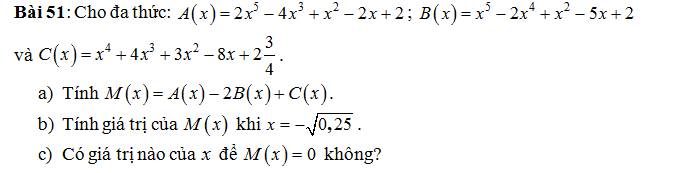
1) \(\dfrac{4^2}{2^3}=\dfrac{\left(2^2\right)^2}{2^3}=\dfrac{2^4}{2^3}=2\)
2) \(\dfrac{25^5}{125^3}=\dfrac{\left(5^2\right)^5}{\left(5^3\right)^3}=\dfrac{5^{10}}{5^9}=5\)
3) \(\dfrac{27^6}{9^9}=\dfrac{\left(3^3\right)^6}{\left(3^2\right)^9}=\dfrac{3^{18}}{3^{18}}=1\)
4) \(\dfrac{16^{13}}{32^{10}}=\dfrac{\left(2^4\right)^{13}}{\left(2^5\right)^{10}}=\dfrac{2^{52}}{2^{50}}=2^2-4\)
5) \(\dfrac{16^5}{64^4}=\dfrac{\left(4^2\right)^5}{\left(4^3\right)^4}=\dfrac{4^{10}}{4^{12}}=\dfrac{1}{4^2}=\dfrac{1}{16}\)
6) \(\dfrac{81^8}{27^{11}}=\dfrac{\left(3^4\right)^8}{\left(3^3\right)^{11}}=\dfrac{3^{32}}{3^{33}}=\dfrac{1}{3}\)
7) \(\dfrac{6^3}{2^3}=\dfrac{2^3\cdot3^3}{2^3}=3^3=27\)
8) \(\dfrac{5^4}{15^3}=\dfrac{5^4}{3^3\cdot5^3}=\dfrac{5}{3^3}=\dfrac{5}{27}\)
9) \(\dfrac{7^{15}}{14^{13}}=\dfrac{7^{15}}{7^{13}\cdot2^{13}}=\dfrac{7^2}{2^{13}}=\dfrac{49}{2^{13}}\)
10) \(\dfrac{\left(-2\right)^6}{24^2}=\dfrac{2^6}{8^2\cdot3^2}=\dfrac{2^6}{\left(2^3\right)^2\cdot3^2}=\dfrac{2^6}{2^6\cdot3^2}=\dfrac{1}{3^2}=\dfrac{1}{9}\)
11: \(\dfrac{27^2}{\left(-18\right)^3}=\dfrac{-3^6}{\left(3^2\cdot2\right)^3}=\dfrac{-3^6}{3^6\cdot2^3}=\dfrac{-1}{8}\)
12: \(\dfrac{\left(-10\right)^8}{8^3\cdot25^4}=\dfrac{2^8\cdot5^8}{2^6\cdot5^8}=2^2=4\)
13: \(\dfrac{4^4\cdot8^3}{16^4}=\dfrac{2^8\cdot2^9}{2^{16}}=2\)
14: \(\dfrac{5^7\cdot9^2}{15^5}=\dfrac{5^7\cdot3^4}{5^5\cdot3^5}=\dfrac{5^2}{3}=\dfrac{25}{3}\)
15: \(\dfrac{21^{13}}{49^6\cdot\left(-27\right)^4}=\dfrac{-7^{13}\cdot3^{13}}{7^{12}\cdot3^{12}}=-7\cdot3=-21\)
16: \(\dfrac{\left(-18\right)^{21}\cdot27^4}{81^{13}\cdot16^5}=\dfrac{-3^{42}\cdot2^{21}\cdot3^{12}}{3^{52}\cdot2^{20}}=\dfrac{-3^{54}}{3^{52}}\cdot2=-3^2\cdot2=-18\)
17: \(\dfrac{45^{14}\cdot8^2}{6^5\cdot125^4\cdot81^6}=\dfrac{3^{28}\cdot5^{14}\cdot2^6}{2^5\cdot3^5\cdot3^{24}\cdot5^{12}}=\dfrac{3^{28}}{3^{29}}\cdot\dfrac{5^{14}}{5^{12}}\cdot\dfrac{2^6}{2^5}=\dfrac{5^2\cdot2}{3}=\dfrac{50}{3}\)
18: \(\dfrac{11\cdot3^{22}\cdot3^7-9^{15}}{\left(2\cdot3^{14}\right)^2}=\dfrac{11\cdot3^{29}-3^{30}}{2^2\cdot3^{28}}=\dfrac{3^{29}\left(11-3\right)}{3^{28}\cdot2^2}=3\cdot\dfrac{8}{4}=3\cdot2=6\)
19: \(\dfrac{8^5\cdot\left(-5\right)^8+\left(-2\right)^5\cdot10^9}{16^4\cdot5^7+20^8}\)
\(=\dfrac{2^{15}\cdot5^8-2^{14}\cdot5^9}{2^{16}\cdot5^7+2^{16}\cdot5^8}=\dfrac{2^{14}\cdot5^8\cdot\left(2-5\right)}{2^{16}\cdot5^7\cdot\left(1+5\right)}=\dfrac{1}{4}\cdot5\cdot\dfrac{-3}{6}=\dfrac{5}{4}\cdot\dfrac{-1}{2}=-\dfrac{5}{8}\)