Cho tứ giác ABCD nội tiếp (O;R) sao cho 2 tiếp tuyến tại B,D và đường thẳng AC đồng quy (AC không đi qua O)
1) Chứng minh rằng : AB.CD = AD.BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(x^2-2x-15=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot-15=64>0\)
Phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{2+\sqrt{64}}{2\cdot1}=5\)
\(x_2=\dfrac{2-\sqrt{64}}{2\cdot1}=-3\)
2) \(x^2-2mx+m-2=0\)
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(m-2\right)=4m^2-4m+8=\left(2m-1\right)^2+7>0\forall m\)
Theo vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-2m\right)}{1}=2m\\x_1x_2=\dfrac{m-2}{1}=m-2\end{matrix}\right.\)
Ta có: \(\left(3+x_1\right)\left(2-x_2\right)-\left(3+x_2\right)\left(x_1-2\right)=x^2_1+x^2_2+18\)
\(\Leftrightarrow6-3x_2+2x_1-x_1x_2-\left(-6+3x_1-2x_2+x_1x_2\right)=x^2_1+x^2_2+18\)
\(\Leftrightarrow6-3x_2+2x_1-x_1x_2+6-3x_1+2x_2-x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2+18\)
\(\Leftrightarrow12-3\left(x_1+x_2\right)+2\left(x_1+x_2\right)-2x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2+18\)
\(\Leftrightarrow12-\left(x_1+x_2\right)=\left(x_1+x_2\right)^2+18\)
\(\Leftrightarrow12-2m=\left(2m\right)^2+18\)
\(\Leftrightarrow12-2m=4m^2+18\)
\(\Leftrightarrow4m^2+2m+6=0\)
\(\Leftrightarrow m\in\varnothing\)
Vậy không có m thỏa mãn

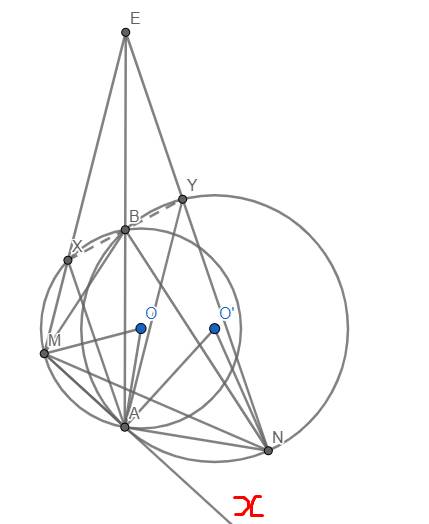
Gọi X và Y lần lượt là giao điểm thứ hai của EM với (O), EN với (O').
Ta có \(\widehat{MAO'}=\widehat{NAO}\left(=90^o\right)\) nên \(\widehat{MAO}=\widehat{NAO'}\). Hơn nữa tam giác MAO và NAO' đều là các tam giác cân nên \(\Rightarrow\widehat{MOA}=\widehat{NO'A}\)
Trong đường tròn (O), ta có: \(\widehat{MOA}=sđ\stackrel\frown{MA}=2.\dfrac{1}{2}sđ\stackrel\frown{MA}=2\widehat{MBA}\)
Tương tự, ta có \(\widehat{NO'A}=2\widehat{ABN}\)
\(\Rightarrow\widehat{MBA}=\widehat{ABN}\)
Hơn nữa có \(\widehat{MAB}=\widehat{ANB}\) (vì chúng lần lượt là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung nhỏ AB của (O').
\(\Rightarrow\Delta BAM\sim\Delta BNA\left(g.g\right)\)
\(\Rightarrow\dfrac{BA}{BN}=\dfrac{BM}{BA}\)
Do \(BA=BE\) nên \(\dfrac{BE}{BN}=\dfrac{BM}{BE}\)
Lại có \(\widehat{MBA}=\widehat{ABN}\left(cmt\right)\) \(\Rightarrow\widehat{EBM}=\widehat{EBN}\)
\(\Rightarrow\Delta MBE\sim\Delta EBN\left(c.g.c\right)\)
\(\Rightarrow\widehat{MEB}=\widehat{ENB}\)
Lại có \(\widehat{ENB}=\widehat{BNY}=\widehat{BAY}\) nên \(\widehat{MEB}=\widehat{BAY}\) \(\Rightarrow\) EX//AY
\(\Rightarrow\widehat{AYN}=\widehat{MEN}\)
Hơn nữa vì \(\widehat{NAx}=\widehat{AYN}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung nhỏ AN trong (O'))
\(\Rightarrow\widehat{NAx}=\widehat{MEN}\)
Từ đó suy ra tứ giác AMEN nội tiếp (góc ngoài bằng góc trong đối)
Ta có đpcm.

A B C E F H M K D I
a/
E và F bình đẳng nhau nên tôi chỉ c/m ME là tiếp tuyến với đường tròn đường kính AH. Còn c/m MF là tiếp tuyến làm tương tự bạn tự c/m nhé
Gọi I là tâm đường tròng đường kính AH => IA=IH
Gọi D là giao của AH với BC
Xét tg ABC có \(AH\perp BC\) (trong tg 3 đường cao đồng quy)
\(\Rightarrow AD\perp BC\)
Xét tg vuông ADC và tg vuông BEC có
\(\widehat{DAC}=\widehat{EBC}\) (cùng phụ với \(\widehat{C}\) ) (1)
Xét tg vuông AHE có
\(IA=IH\Rightarrow IE=IA=IH=\dfrac{AH}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
\(\Rightarrow E\in\left(I\right)\) và tg AIE cân tại I
\(\Rightarrow\widehat{DAC}=\widehat{AEI}\) (góc ở đáy tg cân) (2)
Xét tg vuông BEC có
\(MB=MC\left(gt\right)\Rightarrow ME=MB=MC=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg BME cân tại M
\(\Rightarrow\widehat{EBC}=\widehat{BEM}\) (góc ở đáy tg cân) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{AEI}=\widehat{BEM}\)
Mà \(\widehat{AEI}+\widehat{BEI}=\widehat{AEB}=90^o\)
\(\Rightarrow\widehat{BEM}+\widehat{BEI}=\widehat{MEI}=90^o\Rightarrow ME\perp IE\) => ME là tiếp tuyến với đường tròn đường kính AH
b/
Xét tg MEK và tg MAE có
\(\widehat{AME}\) chung
Ta có
\(sđ\widehat{MEK}=\dfrac{1}{2}sđcungEK\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MAE}=\dfrac{1}{2}sđcungEK\) (góc nội tiếp (O))
\(\Rightarrow\widehat{MEK}=\widehat{MAE}\)
=> tg MEK đồng dạng với tg MAE (g.g.g)
\(\Rightarrow\dfrac{ME}{MA}=\dfrac{MK}{ME}\Rightarrow MK.MA=ME^2\)

\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-m\right)\)
\(=4m^2-4m^2+4m=4m\)
Để phương trình có hai nghiệm dương phân biệt thì \(\left\{{}\begin{matrix}\text{Δ}>0\\-\dfrac{b}{a}>0\\\dfrac{c}{a}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m>0\\2m>0\\m^2-m>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>0\\m\left(m-1\right)>0\end{matrix}\right.\Leftrightarrow m>1\)
\(\sqrt{x_1}=\sqrt{3x_2}\)
=>\(\left\{{}\begin{matrix}x_1>=0\\x_2>=0\\x_1=3x_2\end{matrix}\right.\)
\(x_1+x_2=-\dfrac{b}{a}=2m\)
=>\(3x_2+x_2=2m\)
=>\(x_2=0,5m\)
=>\(x_1=1,5\cdot m\)
\(x_1\cdot x_2=\dfrac{c}{a}=m^2-m\)
=>\(m^2-m-0,75m^2=0\)
=>\(0,25m^2-m=0\)
=>\(m\left(0,25m-1\right)=0\)
=>\(\left[{}\begin{matrix}m=0\left(loại\right)\\m=4\left(nhận\right)\end{matrix}\right.\)
\(\Delta'=m^2-\left(m^2-m\right)=m>0\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-m\end{matrix}\right.\)
Để biểu thức đề bài xác định \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2m>0\\x_1x_2=m^2-m\ge0\end{matrix}\right.\)
\(\Rightarrow m\ge1\)
Khi đó:
\(\sqrt{x_1}=\sqrt{3x_2}\Rightarrow x_1=3x_2\)
Thế vào \(x_1+x_2=2m\Rightarrow4x_2=2m\Rightarrow x_2=\dfrac{m}{2}\)
\(\Rightarrow x_1=\dfrac{3m}{2}\)
Thế vào \(x_1x_2=m^2-m\)
\(\Rightarrow\dfrac{3m^2}{4}=m^2-m\)
\(\Rightarrow m^2-4m=0\Rightarrow\left[{}\begin{matrix}m=0\left(loại\right)\\m=4\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}y\ge\dfrac{3}{2}\\x\ge-5\end{matrix}\right.\)
Từ pt đầu:
\(x^2+6x+9=12y^2-4xy-4x+12y=0\)
\(\Leftrightarrow\left(x^2+4xy+4y^2\right)+10\left(x+2y\right)+25-16\left(y^2+2y+1\right)=0\)
\(\Leftrightarrow\left(x+2y+5\right)^2-\left(4y+4\right)^2=0\)
\(\Leftrightarrow\left(x+6y+9\right)\left(x-2y+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6y+9=0\\x-2y+1=0\end{matrix}\right.\)
- Với \(x+6y+9=0\Leftrightarrow\left(x+5\right)+6y+4=0\) (vô nghiệm do \(x\ge-5\) và \(y\ge\dfrac{2}{3}\))
- Với \(x=2y-1\) thay vào pt dưới:
\(\sqrt{3y-2}-\sqrt{y+2}=2y^2-3y-2\)
\(\Leftrightarrow\dfrac{2\left(y-2\right)}{\sqrt{3y-2}+\sqrt{y+2}}=\left(y-2\right)\left(2y+1\right)\)
\(\Rightarrow\left[{}\begin{matrix}y=2\Rightarrow x=3\\\dfrac{2}{\sqrt{3y-2}+\sqrt{y+2}}=2y+1\left(1\right)\end{matrix}\right.\)
Xét (1), do \(y\ge\dfrac{3}{2}\Rightarrow\dfrac{2}{\sqrt{3y-2}+\sqrt{y+2}}\le\dfrac{2\sqrt{14}}{7}< 2\)
Mà \(2y+1\ge\dfrac{4}{3}+1>2\)
\(\Rightarrow\left(1\right)\) vô nghiệm

a. Với mọi a;b;c ta có:
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca\ge3ab+3bc+3ca\)
\(\Leftrightarrow\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\)
Dấu "=" xảy ra khi \(a=b=c\)
b.
Ta có: \(\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab^2}{2b}=a-\dfrac{ab}{2}\)
Tương tự: \(\dfrac{b}{1+c^2}\ge b-\dfrac{bc}{2}\) ; \(\dfrac{c}{1+a^2}\ge c-\dfrac{ac}{2}\)
Cộng vế:
\(\dfrac{a}{1+b^2}+\dfrac{b}{1+c^2}+\dfrac{c}{1+a^2}\ge a+b+c-\dfrac{ab+bc+ca}{2}\ge a+b+c-\dfrac{\left(a+b+c\right)^2}{6}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

Đề bài chính xác là \(a;b;c>0\) (ko hiểu dấu = có ý nghĩa gì khi mà các mẫu số đều phải khác 0 nên hiển nhiên a;b;c đều khác 0)
Đặt \(P=\dfrac{1}{a^2+b^2+c^2}+\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\)
Do \(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\ge\dfrac{9}{ab+bc+ca}\)
\(\Rightarrow P\ge\dfrac{1}{a^2+b^2+c^2}+\dfrac{9}{ab+bc+ca}\)
\(P\ge\dfrac{1}{a^2+b^2+c^2}+\dfrac{1}{ab+bc+ca}+\dfrac{1}{ab+bc+ca}+\dfrac{7}{ab+bc+ca}\)
\(P\ge\dfrac{9}{a^2+b^2+c^2+2\left(ab+bc+ca\right)}+\dfrac{7}{\dfrac{\left(a+b+c\right)^2}{3}}\)
\(P\ge\dfrac{30}{\left(a+b+c\right)^2}=30\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)

đk: \(-2\le x\le4\)
Ta có \(P^2=\left(\sqrt{x+2}+\sqrt{4-x}\right)^2\)
\(\le2\left[\left(\sqrt{x+2}\right)^2+\left(\sqrt{4-x}\right)^2\right]\) (dùng BĐT \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\))
\(=2\left(x+2+4-x\right)\)
\(=12\)
\(\Rightarrow P\le2\sqrt{3}\) (vì \(P>0\))
Dấu "=" xảy ra \(\Leftrightarrow x+2=4-x\Leftrightarrow x=1\)
Vậy GTLN của P là \(2\sqrt{3}\) khi \(x=1\)
Ta có: \(P=\sqrt{x+2}+\sqrt{4-x}\left(-2\le x\le4\right)\)
\(\Leftrightarrow P^2=\left(\sqrt{x+2}+\sqrt{4-x}\right)^2\)
\(\Leftrightarrow P^2=x+2+4-x+2\sqrt{\left(x+2\right)\left(4-x\right)}\)
\(\Leftrightarrow P^2=6+2\sqrt{\left(x+2\right)\left(4-x\right)}\)
Mà: \(6+2\sqrt{\left(x+2\right)\left(4-x\right)}\le6+x+2+4-x=12\)
\(\Leftrightarrow P^2\le12\)
\(\Leftrightarrow P\le2\sqrt{3}\)
Dấu "=" xảy ra khi: \(x+2=4-x\Leftrightarrow2x=2\Leftrightarrow x=1\)
Vậy: \(P_{max}=2\sqrt{3}\Leftrightarrow x=1\)

Đây là bài toán lãi suất kép trong chương trình 12 chứ ko phải lớp 9
Gọi M là trung điểm của AC và T là điểm đồng quy của 2 tiếp tuyến tại B, D và đường thẳng AC.
Nhận thấy \(\widehat{OBT}=\widehat{ODT}=\widehat{OMT}=90^o\) nên 5 điểm O, M, B, T, D cùng thuộc đường tròn (OT).
Ta có \(\widehat{DCM}=\widehat{DCA}=\widehat{DBA}\)
Và \(\widehat{DMC}=180^o-\widehat{TMD}\) \(=180^o-\widehat{DBT}\) \(=180^o-\widehat{BCD}\) \(=\widehat{DAB}\)
Nên \(\Delta DAB\sim\Delta DMC\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{MC}=\dfrac{BD}{CD}\)
\(\Rightarrow AB.CD=MC.BD=\dfrac{1}{2}AC.BD\)
Tương tự, ta chứng minh được \(AD.BC=\dfrac{1}{2}AC.BD\) (hoặc cùng có thể dùng định lý Ptolemy trong tứ giác ngoại tiếp để suy ra điều này).
\(\Rightarrow AB.CD=AD.BC\left(=\dfrac{1}{2}AC.BD\right)\)
Ta có đpcm.
Mình trả lời rồi nhé bạn. Nếu bạn chưa xem được đáp án thì bạn vào trang cá nhân của mình xem nhé.