
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Mỗi chuyến xe chở số cây là: 6420 : 4 = 1605 (cây)
Tổng số xe tham gia chở cây là: 4 + 5 = 9 (cây)
Tổng số cây mà đội xe đã chở là: 1605 x 9 = 14445 (cây)
14445 < 15000
Vậy đội xe chưa chở đủ số cây đơn vị cần

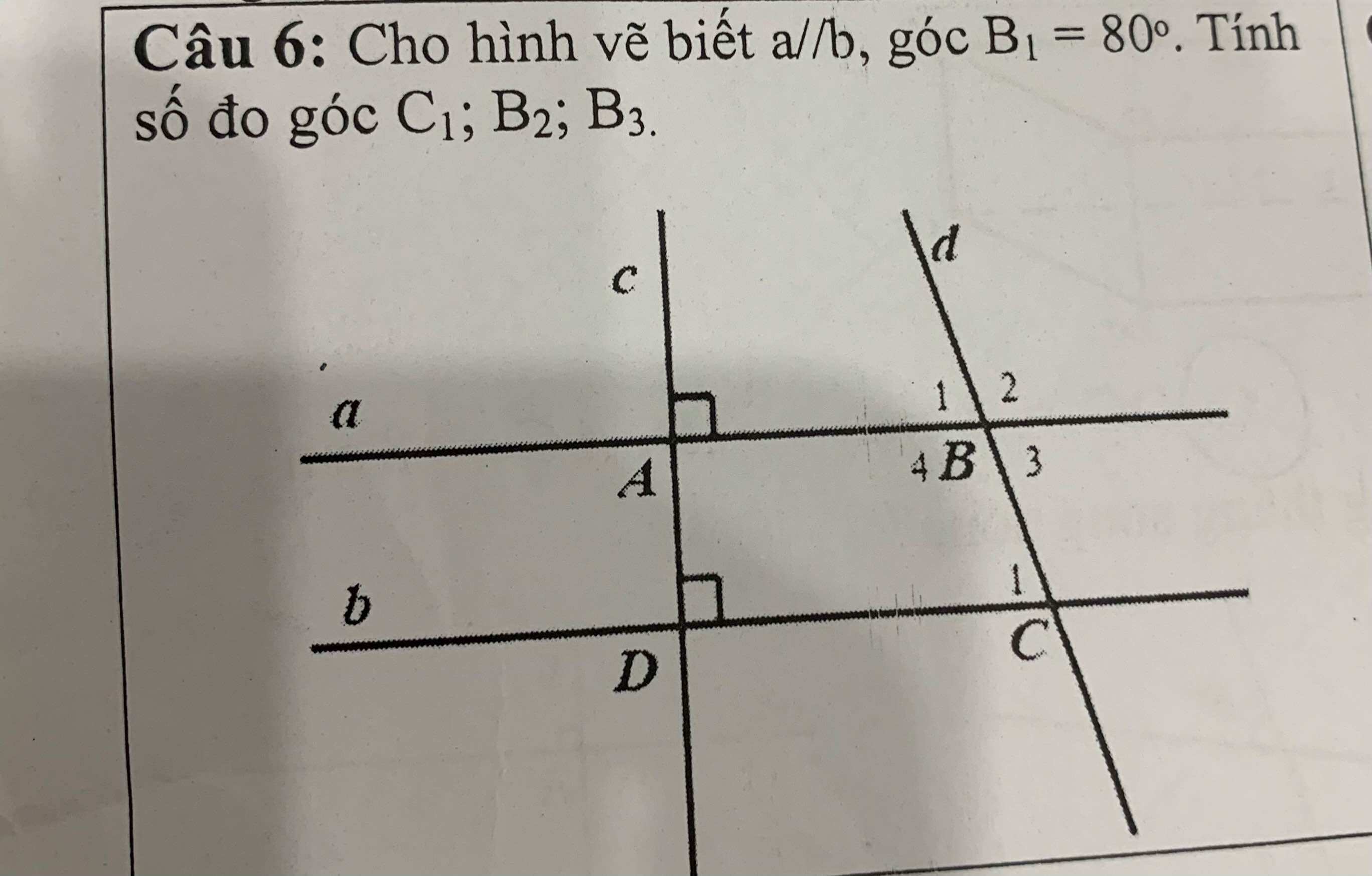
Ta có: \(\widehat{B_1}=\widehat{B_3}\)(hai góc đối đỉnh)
mà \(\widehat{B_1}=80^0\)
nên \(\widehat{B_3}=80^0\)
Ta có: \(\widehat{B_1}+\widehat{B_2}=180^0\)(hai góc kề bù)
=>\(\widehat{B_2}=180^0-80^0=100^0\)
Ta có: a//b
=>\(\widehat{C_1}=\widehat{B_3}\)(hai góc so le trong)
=>\(\widehat{C_1}=80^0\)

Giải đây là toán nâng cao chuyên đề thành phần phép tính, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng suy luận logic như sau:
Giải:
+ Vì tích là số gấp 125 lần thừ số thứ hai nên thừa số nhất là 125
+ Vì nhân một số với 42 nên thừa số thứ hai là 42.
+ Tích của phép nhân là: 125 x 42 = 5250
Đáp số: Thừa số thứ nhất 125; thừa số thứ hai là 42; tích là: 5250

A = 20240 + 20242025 + 20242026 + 20242027 + 20242028
A = 1 + (20242025 + 20242026) + (20242027 + 20242028)
A = 1 + 20242025.(1 + 2024) + 20242027.(1+ 2024)
A = 1 + (1 + 2024)(20242025 + 20242027)
A = 1 + 2025.(20242025 + 20242027)
2025 ⋮ 2025; 1 : 2025 dư 1
⇒ A : 2025 dư 1
Kết luận A chia 2025 dư 1

Kí hiệu số mũ trong lũy thừa mà học sinh hay dùng là ^
Ví dụ 2 lũy thừa 3 = 2^3

Giải:
a; Mô tả yếu tố cơ bản của hình vuông:
* Các cạnh của hình vuông bằng nhau
* Bốn góc hình vuông bằng nhau và bằng 900
* Đường chéo của hình vuông:
+ Hai đường chéo hình vuông bằng nhau
+ Hai đường chéo hình vuông vuông góc với nhau
+ Hai đường chéo hình vuông cắt nhau tại trung điểm của mỗi đường.
b; Mô tả nền nhà hình chữ nhật có kích thước 8m, 6m
Diện tích của nền nhà là: 8 x 6 = 48 (m2)
Kết luận diện tích căn nhà là 48m2

Đây là toán nâng cao chuyên đề giải phương trình chứa dấu giá trị tuyệt đối, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp lập bảng như sau:
Giải:
\(x\) + 1 = 0 ⇒ \(x=-1\); \(x+2\) = 0 ⇒ \(x\) = -2
Lập bảng ta có:
| \(x\) | -2 -1 |
| |\(x+1\)| | - \(x-1\) | - \(x-1\) 0 \(x+1\) |
| |\(x+2\)| | - \(x-2\) 0 \(x+2\) | \(x+2\) |
| |\(x\) + 1| + |\(x+2\)| | - 2\(x\) - 3 | 1 | 2\(x\) + 3 |
Theo bảng trên ta có:
TH1 : nếu \(x\) < - 2 ta có:
- 2\(x\) - 3 = 9 ⇒ 2\(x\) = - 3 - 9 = - -12 ⇒ \(x=-12:2\) = - 6
TH2: Nếu -2 ≤ \(x\) ≤ - 1 ta có: 1 = 9 (vô lý)
TH3: Nếu - 1 ≤ \(x\) ta có: 2\(x\) + 3 = 9 ⇒2\(x\) = 9 - 3 = 6⇒ \(x=6:2=3\)
Kết hợp các trường hợp trên ta có: \(x\) = -6; \(x=3\)
Vậy \(x\in\) {-6; 3}


Bài 1:
\(2x+1\) ⋮ \(x\) - 1 (\(x\) \(\in\) N)
2(\(x\) - 1) + 3 ⋮ \(x-1\)
3 ⋮ \(x-1\)
\(x-1\) \(\in\) Ư(3) = [-3; -1; 1; 3}
Lập bảng ta có:
| \(x-1\) | -3 | -1 | 1 | 3 |
| \(x\) | -2 | 0 | 2 | 4 |
| \(x\in\) N | loại | nhận | nhận | nhận |
Theo bảng trên ta có: \(x\) \(\in\) {0; 2; 4}
Vậy \(x\) \(\in\) {0; 2; 4}
Bài 2:
Vì số đó chia cho 15 được dư là 9 nên số đó có dạng:
15k + 9 (k \(\in\) N)
15k + 9 = 3(5k + 3) ⋮ 3
15k ⋮ 5; 9 không chia hết cho 5 nên số đó không chia hết cho 5
Kết luận số đó chia hết cho 3 nhưng không chia hết cho 5
Giải:
Tổng số cân nặng của tất cả các quả mít là:
4,8 + 3,19 + 2,13 + 5,8 + 6,63 + 3,25 + 4,3 + 3,9 = 34 (kg)
Cân nặng của quả mít mà Rô - bốt đã bỏ qua là:
34 - 31,87 = 2,13 (kg)
Quả Rô - bôt đã quên là: quả mít C.
WUT