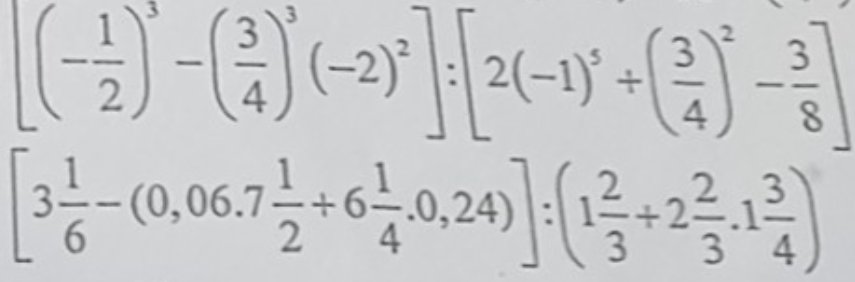
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
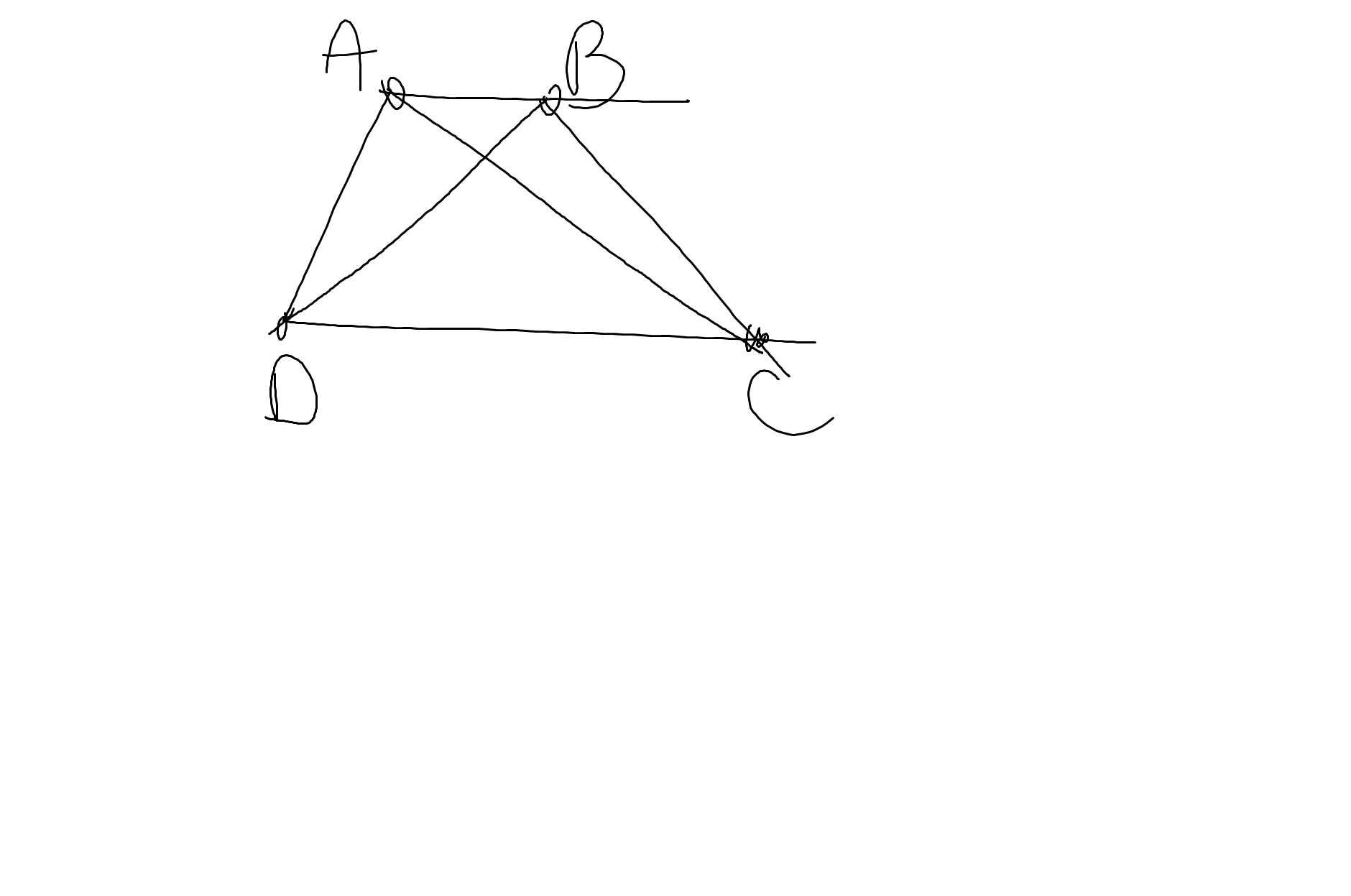
a: Hai cạnh đáy là AB,CD
Hai cạnh bên là AD,BC
b: Các cặp góc kề cạnh đáy là:
\(\widehat{BAD};\widehat{ABC}\)
\(\widehat{ADC};\widehat{BCD}\)
Các cặp góc kề cạnh bên là:
\(\widehat{BAD};\widehat{ADC}\)
\(\widehat{ABC};\widehat{BCD}\)
c: Hai đường chéo là AC,BD
Bài 2:
a: Ta có: ΔDAC vuông cân tại D
=>\(\widehat{DAC}=\widehat{DCA}=45^0\)
Ta có: ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
Ta có: \(\widehat{DAC}=\widehat{ACB}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//CB
=>ABCD là hình thang
Hình thang ABCD có AD\(\perp\)DC
nên ABCD là hình thang vuông
b: ABCD là hình thang vuông có hai đáy là AD,CB và AD\(\perp\)DC
=>CB\(\perp\)CD
=>\(\widehat{ADC}=\widehat{DCB}=90^0\)
Ta có: AD//CB
=>\(\widehat{DAB}+\widehat{ABC}=180^0\)
=>\(\widehat{DAB}=180^0-45^0=135^0\)

Bài 1:
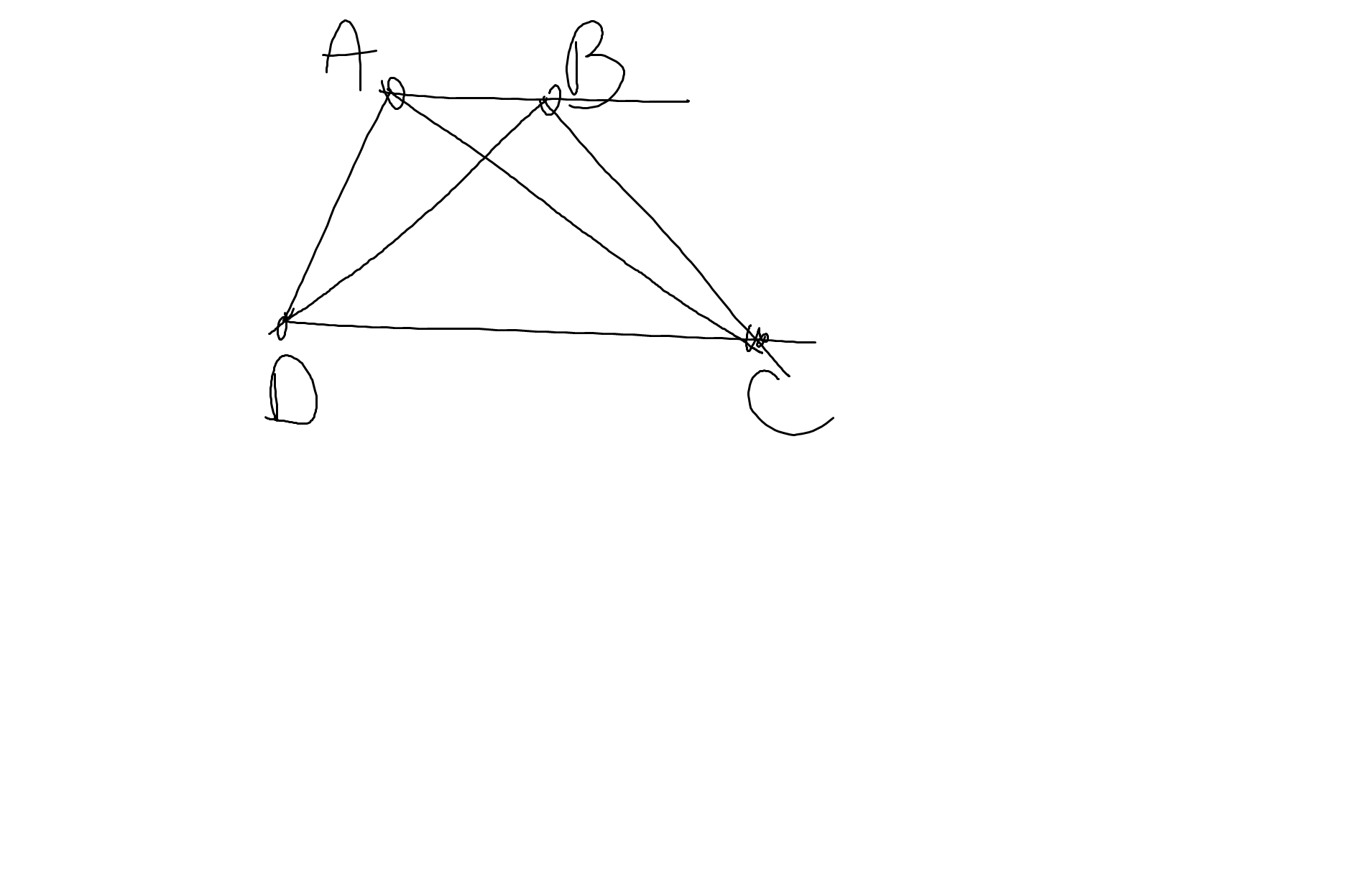
a: Hai cạnh đáy là AB,CD
Hai cạnh bên là AD,BC
b: Các cặp góc kề cạnh đáy là:
\(\widehat{BAD};\widehat{ABC}\)
\(\widehat{ADC};\widehat{BCD}\)
Các cặp góc kề cạnh bên là:
\(\widehat{BAD};\widehat{ADC}\)
\(\widehat{ABC};\widehat{BCD}\)
c: Hai đường chéo là AC,BD
Bài 2:
a: Ta có: ΔDAC vuông cân tại D
=>\(\widehat{DAC}=\widehat{DCA}=45^0\)
Ta có: ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
Ta có: \(\widehat{DAC}=\widehat{ACB}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//CB
=>ABCD là hình thang
Hình thang ABCD có AD\(\perp\)DC
nên ABCD là hình thang vuông
b: ABCD là hình thang vuông có hai đáy là AD,CB và AD\(\perp\)DC
=>CB\(\perp\)CD
=>\(\widehat{ADC}=\widehat{DCB}=90^0\)
Ta có: AD//CB
=>\(\widehat{DAB}+\widehat{ABC}=180^0\)
=>\(\widehat{DAB}=180^0-45^0=135^0\)

a)
\(\dfrac{8}{9}-\dfrac{1}{72}-\dfrac{1}{56}-\dfrac{1}{42}-\dfrac{1}{30}-\dfrac{1}{20}-\dfrac{1}{12}-\dfrac{1}{6}-\dfrac{1}{2}\\ =\dfrac{8}{9}-\left(\dfrac{1}{72}+\dfrac{1}{56}+\dfrac{1}{42}+\dfrac{1}{30}+\dfrac{1}{20}+\dfrac{1}{12}+\dfrac{1}{6}+\dfrac{1}{2}\right)\\ =\dfrac{8}{9}-\left(\dfrac{1}{8\cdot9}+\dfrac{1}{7\cdot8}+\dfrac{1}{6\cdot7}+\dfrac{1}{6\cdot5}+\dfrac{1}{4\cdot5}+\dfrac{1}{3\cdot4}+\dfrac{1}{2\cdot3}+\dfrac{1}{1\cdot2}\right)\\ =\dfrac{8}{9}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\right)\\ =\dfrac{8}{9}-\left(1-\dfrac{1}{9}\right)\\ =\dfrac{8}{9}-\dfrac{8}{9}\\ =0\)
b)
\(\left(-\dfrac{1}{2}\right)-\left(\dfrac{-3}{5}\right)+\left(-\dfrac{1}{9}\right)+\dfrac{1}{127}-\dfrac{7}{18}+\dfrac{4}{35}-\left(\dfrac{-2}{7}\right)\\ =\left(-\dfrac{1}{2}-\dfrac{1}{9}-\dfrac{7}{18}\right)+\left(\dfrac{3}{5}+\dfrac{2}{7}+\dfrac{4}{35}\right)+\dfrac{1}{127}\\ =\dfrac{-9-2-7}{18}+\dfrac{21+10+4}{35}+\dfrac{1}{127}\\ =-1+1+\dfrac{1}{127}\\ =\dfrac{1}{127}\)
c) (*sửa*)
\(\dfrac{3}{5}+\dfrac{3}{11}-\dfrac{-3}{7}+\dfrac{2}{97}-\dfrac{1}{35}-\dfrac{3}{4}-\dfrac{23}{44}\\ =\dfrac{3}{5}+\dfrac{3}{11}+\dfrac{3}{7}+\dfrac{2}{97}-\dfrac{1}{35}-\dfrac{3}{4}+\dfrac{23}{44}\\ =\left(\dfrac{3}{5}+\dfrac{3}{7}-\dfrac{1}{35}\right)+\left(\dfrac{3}{11}-\dfrac{3}{4}-\dfrac{23}{44}\right)+\dfrac{2}{97}\\ =\dfrac{21+15-1}{35}+\dfrac{12-33-23}{44}+\dfrac{2}{97}\\ =1+\left(-1\right)+\dfrac{2}{97}\\ =\dfrac{2}{97}\)

\(x^2+5xy+6y^2+x+2y-2=0\)
\(\Leftrightarrow x^2+2xy+3xy+6y^2+x+2y=2\)
\(\Leftrightarrow x\left(x+2y\right)+3y\left(x+2y\right)+\left(x+2y\right)=2\)
\(\Leftrightarrow\left(x+2y\right)\left(x+3y+1\right)=2\)
Ta xét các TH sau:
TH1: \(\left\{{}\begin{matrix}x+2y=1\\x+3y+1=2\end{matrix}\right.\Leftrightarrow\left(x;y\right)=\left(1;0\right)\)
TH2: \(\left\{{}\begin{matrix}x+2y=2\\x+3y+1=1\end{matrix}\right.\Leftrightarrow\left(x;y\right)=\left(6;-2\right)\)
TH3: \(\left\{{}\begin{matrix}x+2y=-1\\x+3y+1=-2\end{matrix}\right.\Leftrightarrow\left(x;y\right)=\left(3;-2\right)\)
TH4: \(\left\{{}\begin{matrix}x+2y=-2\\x+3y+1=-1\end{matrix}\right.\Leftrightarrow\left(x;y\right)=\left(-2;0\right)\)
Vậy có 4 cặp số (x; y) thỏa mãn đề bài là \(\left(1;0\right),\left(6;-2\right),\left(3;-2\right),\left(-2;0\right)\)

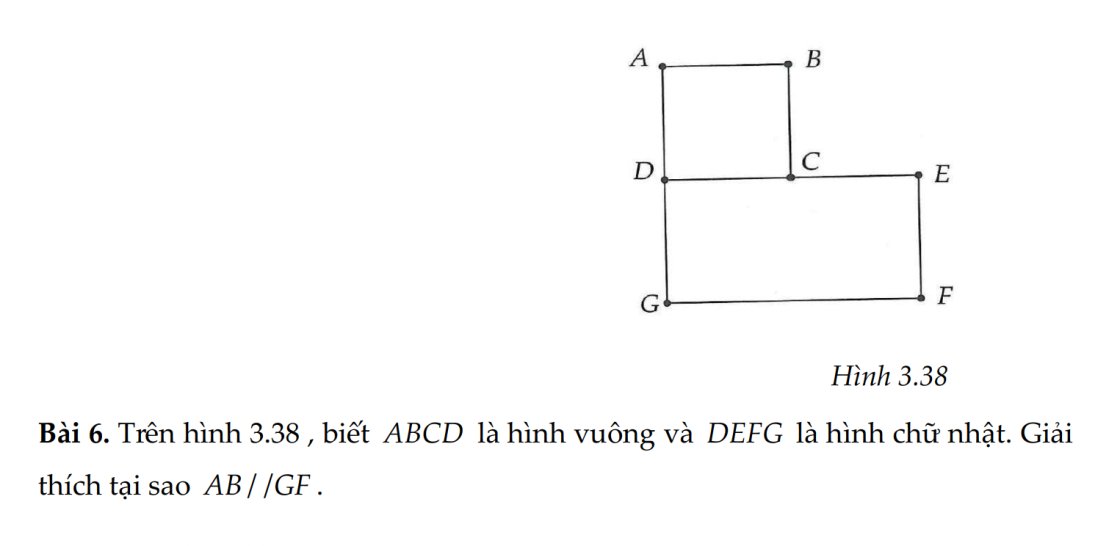
ABCD là hình vuông
=>AB//CD
mà C\(\in\)DE
nên AB//DE
Ta có: DEFG là hình chữ nhật
=>DE//FG
mà AB//DE
nên AB//FG

a)
\(32< 2^x< 128\\ =>2^5< 2^x< 2^7\\ =>5< x< 7\\ =>x=6\)
b)
\(2\cdot16\ge2^x>4\\ =>2\cdot2^4\ge2^x>2^2\\ =>2^5\ge2^x>2^2\\ =>5\ge x>2\\ =>x\in\left\{3;4;5\right\}\)
c)
\(9\cdot27\le3^x\le243\\ =>3^2\cdot3^3\le3^x\le3^5\\ =>3^5\le3^x\le3^5\\ =>5\le x\le5\\ =>x=5\)
d)
\(x^{2019}=x\\ =>x^{2019}-x=0\\ =>x\left(x^{2018}-1\right)=0\)
TH1: x = 0
TH2: `x^2018-1=0`
`=>x^2018=1`
`=>x^2018=1^2018`
`=>x=1` hoặc `x=-1`
a: \(32< 2^x< 128\)
=>\(2^5< 2^x< 2^7\)
=>5<x<7
mà x là số tự nhiên
nên x=6
b: \(2\cdot16>=2^x>4\)
=>\(2^5>=2^x>2^2\)
=>2<x<=5
mà x là số tự nhiên
nên \(x\in\left\{3;4;5\right\}\)
c: \(9\cdot27< =3^x< =243\)
=>\(243< =3^x< =243\)
=>\(3^x=243=3^5\)
=>x=5
d: \(x^{2019}=x\)
=>\(x\left(x^{2018}-1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x^{2018}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^{2018}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
e: \(2^{x+1}+4\cdot2^x=3\cdot2^7\)
=>\(2^x\cdot2+4\cdot2^x=6\cdot2^6\)
=>\(6\cdot2^x=6\cdot2^6\)
=>x=6
f: \(2^{2x}+2^{2x+3}=3^2\cdot8^4\)
=>\(2^{2x}+2^{2x}\cdot8=9\cdot8^4\)
=>\(9\cdot2^{2x}=9\cdot2^{12}\)
=>2x=12
=>x=6
g: \(27^{x+1}=9^{x+5}\)
=>\(3^{3\left(x+1\right)}=3^{2\left(x+5\right)}\)
=>3(x+1)=2(x+5)
=>3x+3=2x+10
=>3x-2x=10-3
=>x=7
h: \(3^{x+2}+5\cdot3^{x+1}=648\)
=>\(3^x\cdot9+5\cdot3^x\cdot3=648\)
=>\(3^x\cdot24=648\)
=>\(3^x=\dfrac{648}{24}=27=3^3\)
=>x=3

\(\left(1:\dfrac{1}{7}\right)^2\left[\left(2^2\right)^3:2^5\right]\cdot\dfrac{1}{49}\\ =7^2\left(2^6:2^5\right)\cdot\dfrac{1}{7^2}\\=\left(7^2\cdot\dfrac{1}{7^2}\right)\cdot2^{6-5}\\ =1\cdot2^1\\ =2\)
\(\left(1:\dfrac{1}{7}\right)^2\left[\left(2^2\right)^3:2^5\right]\cdot\dfrac{1}{49}\)
\(=\dfrac{7^2}{49}\cdot\left(2^6:2^5\right)\)
\(=\dfrac{49}{49}\cdot2=2\)
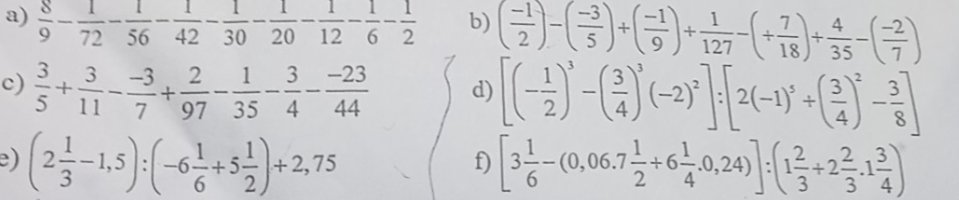
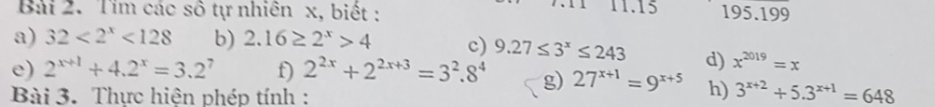
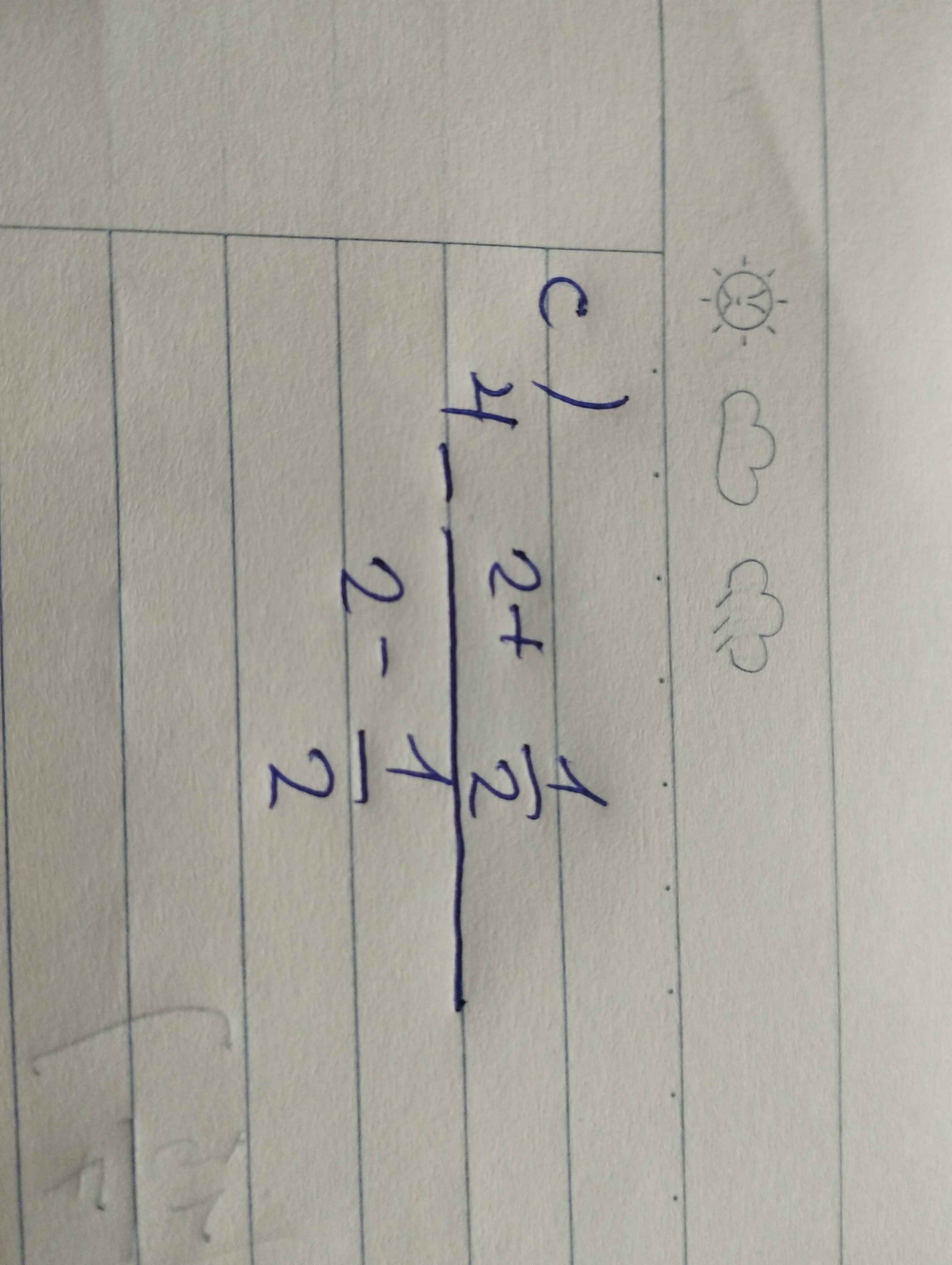
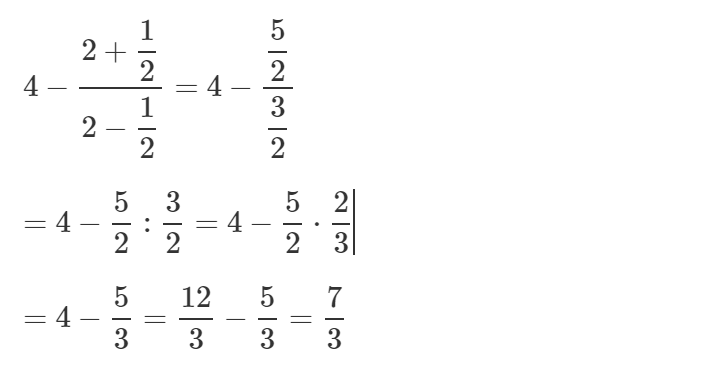
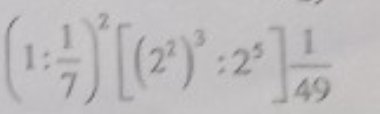
\(\left[\left(-\dfrac{1}{2}\right)^3-\left(\dfrac{3}{4}\right)^3\cdot\left(-2\right)^2\right]:\left[2\cdot\left(-1\right)^5+\left(\dfrac{3}{4}\right)^2-\dfrac{3}{8}\right]\\ =\left(-\dfrac{1}{8}-\dfrac{27}{64}\cdot4\right):\left(2\cdot-1+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(-\dfrac{1}{8}-\dfrac{27}{16}\right):\left(-2+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(\dfrac{-2}{16}-\dfrac{27}{16}\right):\left(\dfrac{-32}{16}+\dfrac{9}{16}-\dfrac{6}{16}\right)\\ =\dfrac{-29}{16}:\dfrac{-29}{16}\\ =1\)
____________________________
\(\left[3\dfrac{1}{6}-\left(0,06\cdot7\dfrac{1}{2}+6\dfrac{1}{4}\cdot0,24\right)\right]:\left(1\dfrac{2}{3}+2\dfrac{2}{3}\cdot1\dfrac{3}{4}\right)\\ =\left[\dfrac{19}{6}-\left(0,06\cdot\dfrac{15}{2}+\dfrac{25}{4}\cdot4\cdot0,06\right)\right]:\left(\dfrac{5}{3}+\dfrac{8}{3}\cdot\dfrac{7}{4}\right)\\ =\left[\dfrac{19}{6}-0,06\cdot\left(\dfrac{15}{4}+25\right)\right]:\left(\dfrac{5}{3}+\dfrac{14}{3}\right)\\ =\left(\dfrac{19}{6}-0,06\cdot\dfrac{65}{2}\right):\dfrac{19}{3}\\ =\left(\dfrac{19}{6}-\dfrac{39}{20}\right):\dfrac{19}{3}\\ =\dfrac{73}{60}:\dfrac{19}{3}\\ =\dfrac{73}{380}\)