Bài học cùng chủ đề
- Trường hợp đồng dạng thứ nhất của tam giác (c.c.c)
- Trường hợp đồng dạng thứ nhất của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ nhất của hai tam giác (vận dụng)
- Trường hợp đồng dạng thứ hai của tam giác (c.g.c)
- Trường hợp đồng dạng thứ hai của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ hai của hai tam giác (vận dụng)
- Trường hợp đồng dạng thứ ba của tam giác (g.g)
- Trường hợp đồng dạng thứ ba của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ ba của hai tam giác (nâng cao)
- Trường hợp bằng nhau thứ nhất của hai tam giác
- Trường hợp bằng nhau thứ hai của hai tam giác
- Trường hợp bằng nhau thứ ba của hai tam giác
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Trường hợp đồng dạng thứ ba của tam giác (g.g) SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
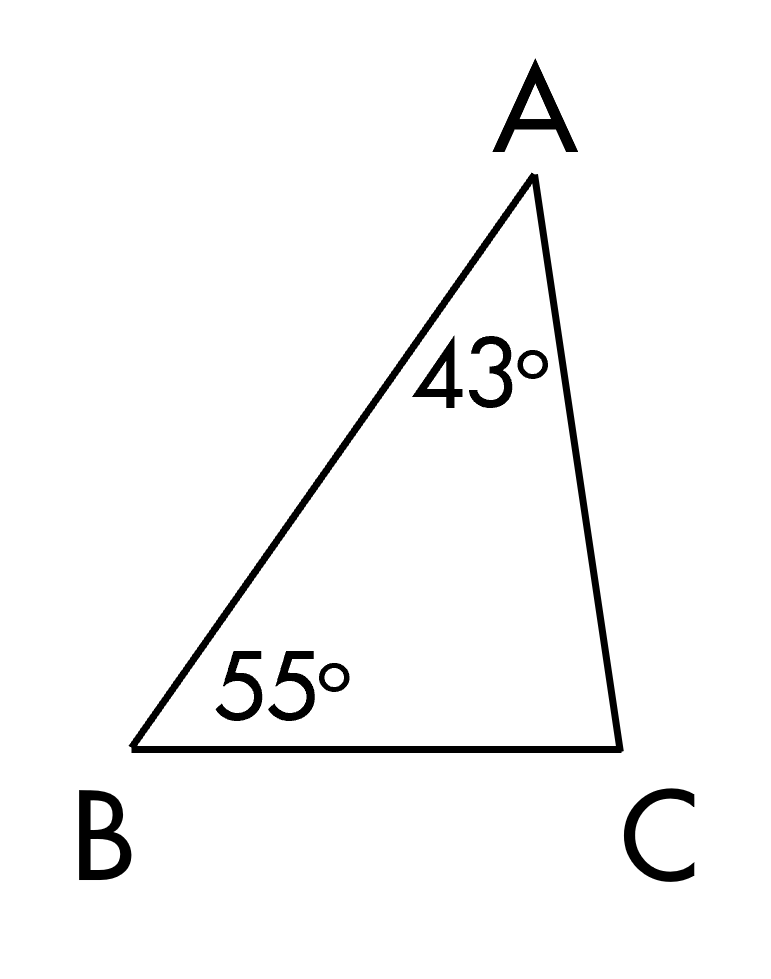
Cho hình vẽ. C= ∘.
Câu 2 (1đ):
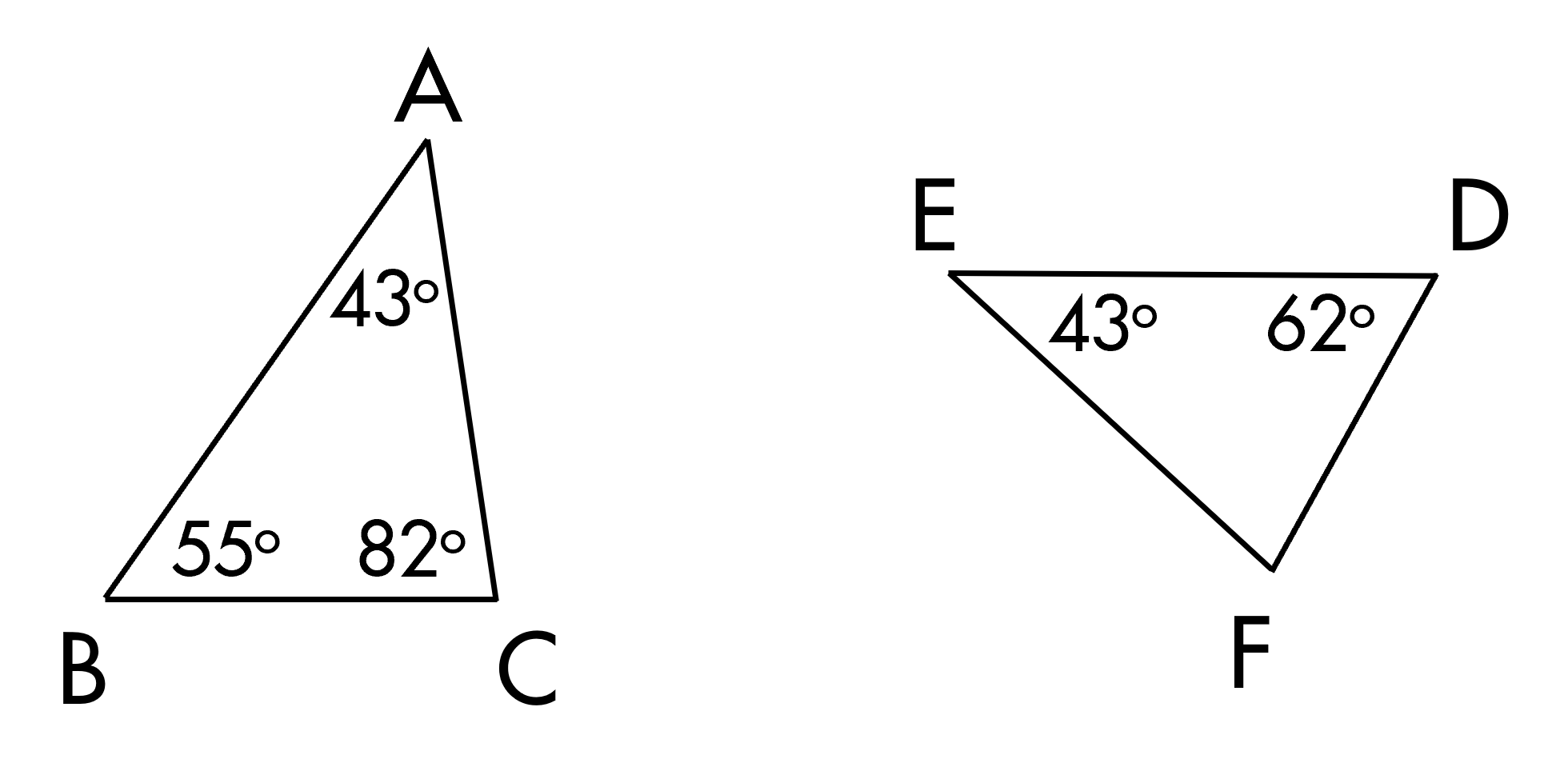
Cho hình vẽ, ΔABC và ΔDEF có bao nhiêu cặp góc bằng nhau (mỗi góc chọn ở một tam giác)?
0.
1.
2.
Câu 3 (1đ):
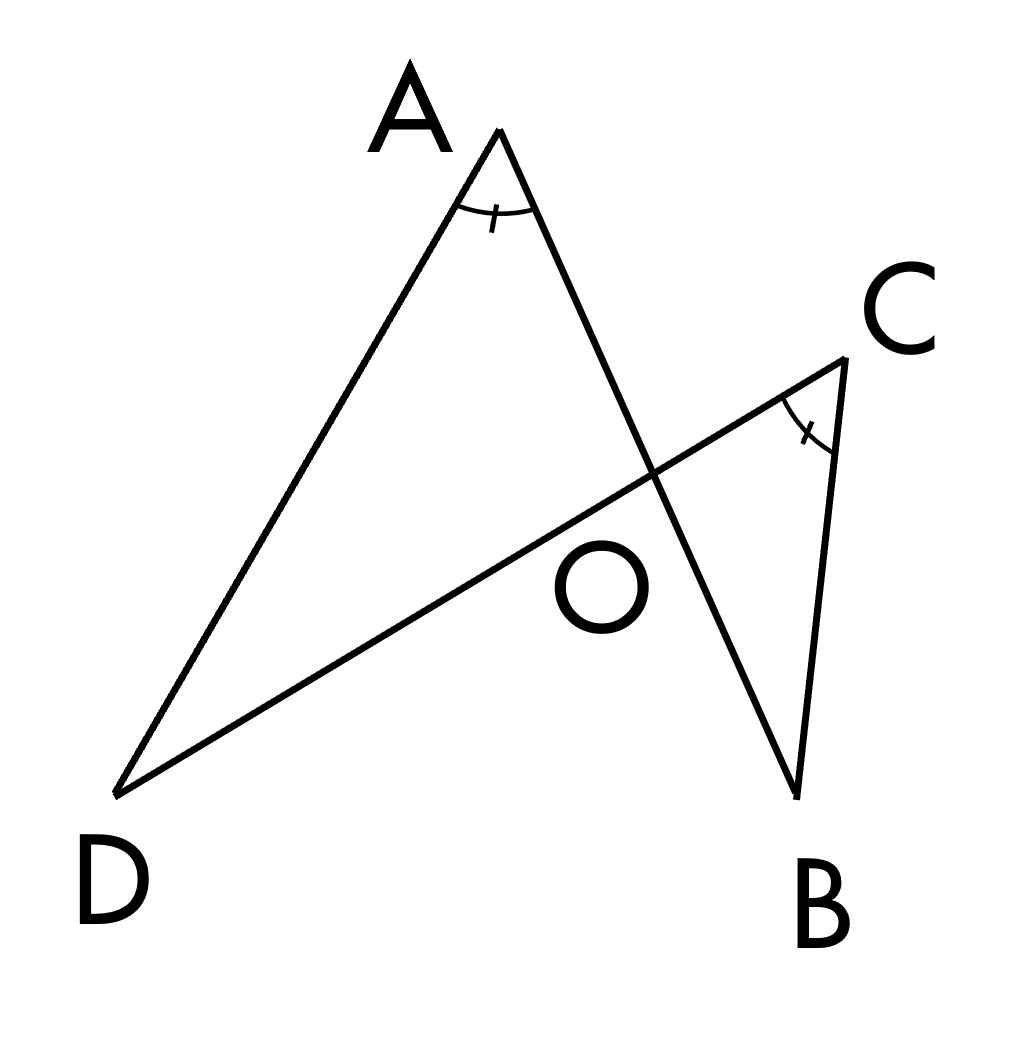
Cho hình vẽ. Kéo thả phương án đúng vào ô trống.
Xét ΔOAD và ΔCOB có:
A= .
AOD= .
Vậy ΔOAD∽ΔOCB (g.g).
AOCCBOCB
(Kéo thả hoặc click vào để điền)
Câu 4 (1đ):
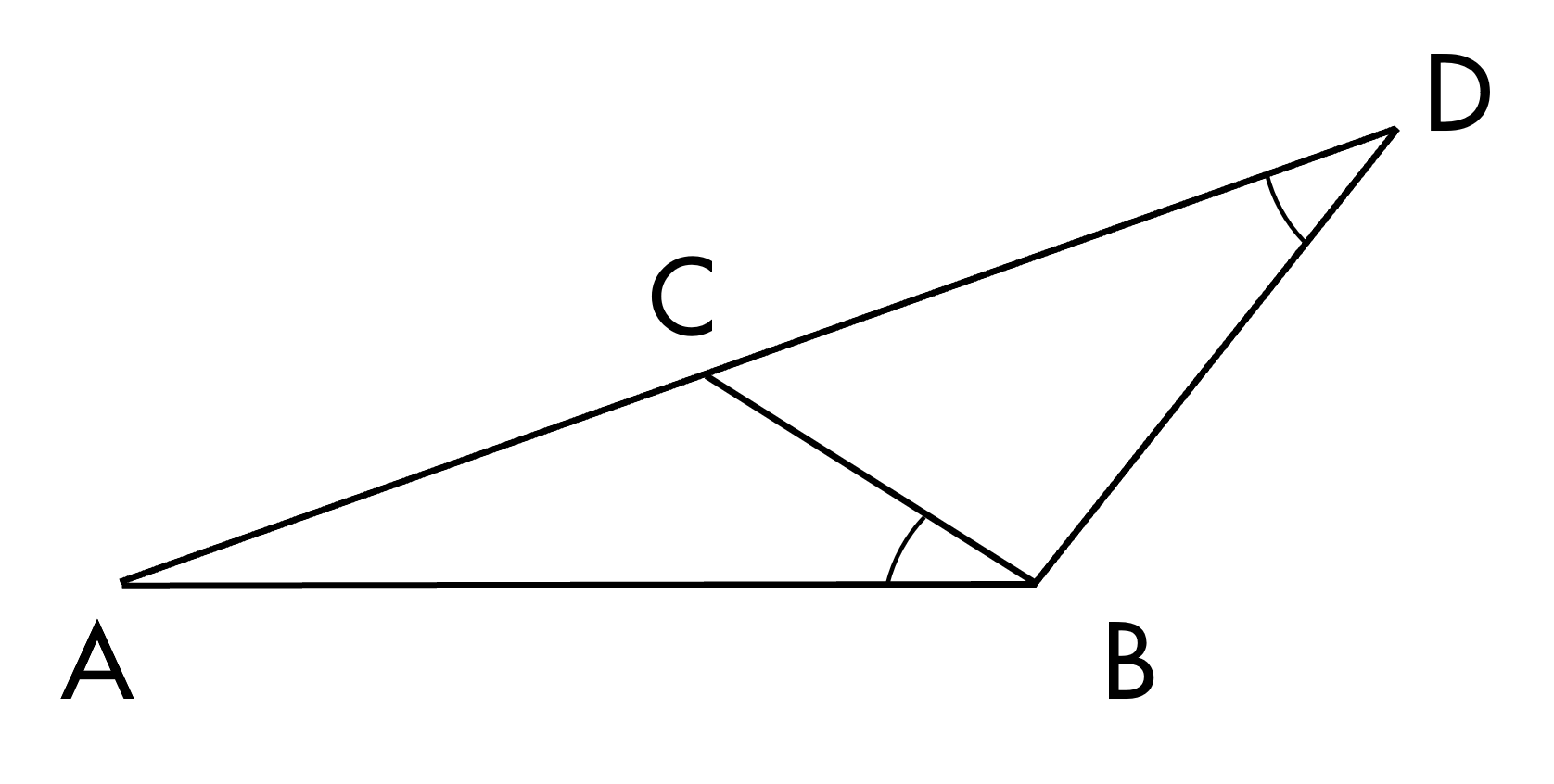
Cho hình vẽ. Tỉ lệ thức ACAB=ABAD được suy ra từ cặp tam giác đồng dạng nào?
ΔADB∽ΔCDB.
ΔABC∽ΔADB.
ΔABC∽ΔCDB.
Câu 5 (1đ):
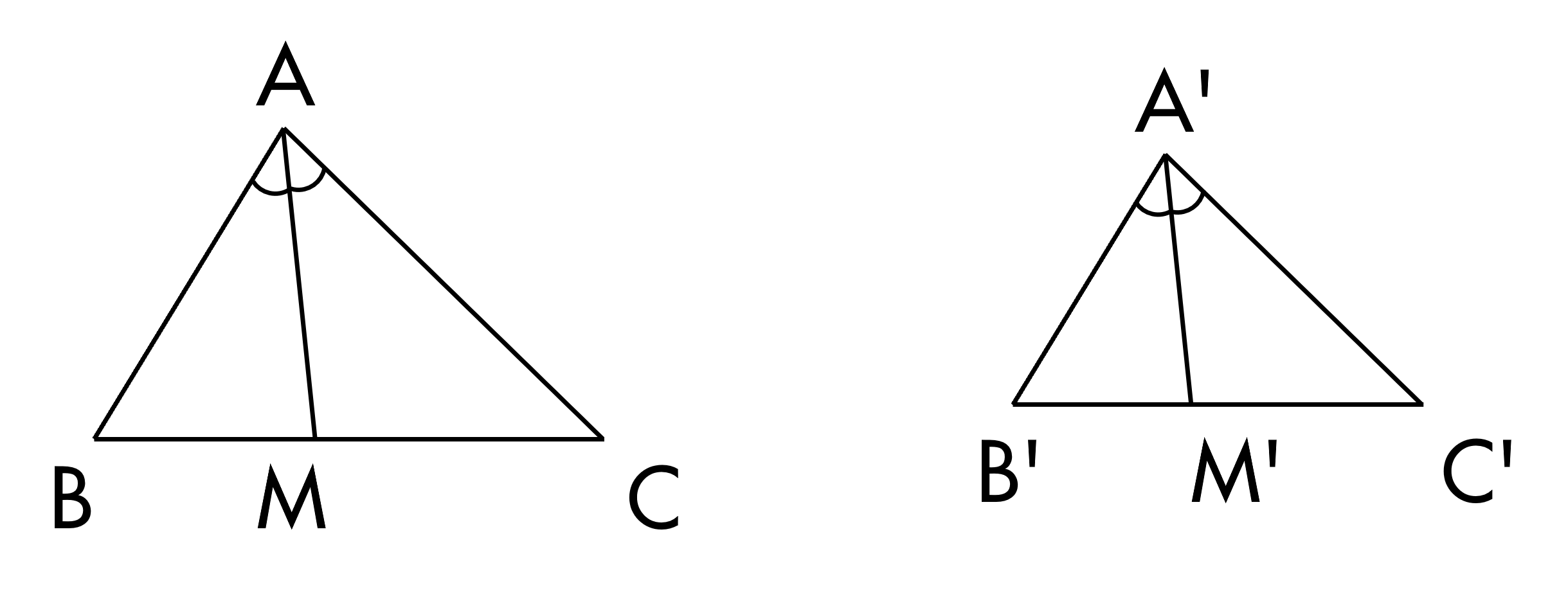
Cho hình vẽ. Tỉ lệ thức AMA′M′=ABA′B′ được suy ra từ cặp tam giác đồng dạng nào?
ΔAMC∽ΔA′M′C′.
ΔA′B′M′∽ΔABM.
ΔA′B′C′∽ΔABC.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- [âm nhạc]
- sang đến phần cuối cùng chúng ta sẽ cùng
- nhau tìm hiểu về trường hợp đồng dạng
- thứ ba của tam giác trường hợp góc
- góc nội dung của định lý về trườ hợp
- đồng dạng thứ ba của tam giác như sau
- nếu hai góc của tam giác này lần lượt
- bằng hai góc của tam giác kia thì hai
- tam giác đó đồng dạng với
- nhau thầy sẽ Viết giả thiết và kết luận
- của định lý cho tam giác ABC và tam giác
- DEF Nếu góc A bằng góc D và góc B bằng
- góc e thì chúng ta kết luận được ngay
- tam giác ABC đồng dạng với tam giác
- DEF bây giờ thầy sẽ nói qua về hướng
- chứng minh của định lý này chúng ta sẽ
- chứng minh định lý này ở trong trường
- hợp độ dài cạnh AB khác độ dài cạnh de
- vì nếu như AB bằng DE thì hai tam giác
- này bằng nhau từ đó ta suy ra ngay hai
- tam giác này đồng
- dạng trong trường hợp AB khác de thì
- hướng chứng minh của chúng ta cũng giống
- như hai trường hợp trước đó là ta sử
- dụng định lý về tam giác đồng dạng dựng
- một tam giác bằng tam giác DEF và đồng
- dạng với tam giác
- ABC cụ thể hơn ta sẽ dựng như sau lấy
- điểm M thuộc vào đoạn AB sao cho AM =
- de từ m kẻ MN song song với BC và cắt AC
- tại
- N ta thấy góc M bằ Góc B vì hai góc này
- ở vị trí đồng
- vị từ đây ta chứng minh được tam giác
- ABC đồng dạng với tam giác amn theo định
- lý về tam giác đồng dạng hơn nữa ta cũng
- chứng minh được tam giác amn lại bằng
- với tam giác DEF theo trường hợp góc
- cạnh góc đến đây chúng ta sử dụng tính
- chất bắc cầu có tam giác ABC đồng dạng
- với tam giác amn mà tam giác amn lại
- đồng dạng với tam giác daf f thì ta suy
- ra ngay tam giác ABC đồng dạng với tam
- giác DEF và ta có điều phải chứng
- minh bây giờ chúng ta sẽ đến với một số
- bài tập áp dụng trường hợp đồng dạng thứ
- ba của tam giác trường hợp góc
- góc hỏi chấm ha tam giác nào dưới đây
- đồng dạng với tam giác
- ABC thầy có ba tam giác như ở trên hình
- để tiện cho việc kiểm tra tam giác nào
- đồng dạng với tam giác abc theo trường
- hợp góc góc thì chúng ta sẽ tính số đo
- của góc
- C cụ thể hơn trong tam giác ABC ta có
- góc A cộng góc B cộng góc C = 180 độ
- Theo định lý tổng ba góc của một tam
- giác từ đây ta tính ra ngay góc C sẽ
- bằng 82
- độ bây giờ chúng ta sẽ kiểm tra hai tam
- giác ABC và
- DEF chúng ta thấy hai tam giác này không
- có hai góc nào bằng nhau Do đó hai tam
- giác này không phải là hai tam giác đồng
- dạng
- tiếp theo chúng ta sẽ kiểm tra hai tam
- giác ABC và tam giác
- mnl xét tam giác ABC và tam giác nml ta
- thấy có góc C bằng với góc L bằng 82 độ
- góc b bằng với góc m bằng 55 Độ do đó
- tam giác ABC đồng dạng với tam giác nml
- theo trường hợp góc
- góc như vậy là chúng ta đã hoàn thành
- hỏi
- CH2 sang đến hỏi ch3 cho hình vẽ
- câu a chứng minh tam giác oad đồng dạng
- với tam giác
- OCB oad
- OCB câu b Chứng minh oa nhân OB bằng OC
- nh
- OD chúng ta thấy ngay được hai tam giác
- này đồng dạng với nhau theo trường hợp
- góc góc xét tam giác oad và tam giác OCB
- có góc A bằng góc
- C góc aod bằng với góc cob do hai góc
- đối đỉnh
- như vậy ta kết luận được ngay tam giác
- aod đồng dạng với tam giác OCB theo
- trường hợp góc
- góc tiếp theo chúng ta sãy sang câu b ở
- câu b này chúng ta thấy ở đây là đẳng
- thức của tích hai cạnh bằng nhau và đẳng
- thức này được suy ra trực tiếp từ kết
- quả của câu
- a vì tam giác oad đồng dạng với tam giác
- OCB nên ta có ngay oa tr OC bằ OD tr OB
- Đây là hai cặp cạnh tướng tỉ lệ và hơn
- nữa chúng ta sẽ khéo léo chọn ra các
- cạnh sao cho chúng xuất hiện ở trong
- đẳng thức này đến đây áp dụng tính chất
- tỉ lệ thức ta được oa nhân OB bằng OC nh
- OD ta có điều phải chứng
- minh như vậy là ta đã hoàn thành hỏi
- ch3 sang đến hỏi CH4 cho các điểm ABCD
- như hình vẽ biết rằng góc abc bằng với
- góc
- ADB Chứng minh rằng AB bình phương bằng
- AD nh
- AC đề bài yêu cầu chúng ta chứng minh
- đẳng thức với mỗi vế là tích của hai
- cạnh và hướng làm của bài này chúng ta
- sẽ đưa đẳng thức này về dạng hai tỷ số
- bằng
- nhau cụ thể hơn từ AB bình phương bằng
- AD nh
- AC ta đưa về AB tr AC bằng AD tr AB đến
- đây chúng ta sẽ suy nghĩ đến việc lựa
- chọn hai tam giác đồng dạng để suy ra
- cặp tỉ số
- này ta sẽ chọn tam giác chứa hai cạnh AB
- và AD đó ra tam giác
- ABD tam giác thứ hai là tam giác chứa
- hai cạnh AC và AB đó là tam giác
- ABC như vậy ta cần chứng minh tam giác
- ABC đồng dạng với tam giác
- ADB xét tam giác ABC và tam giác ADB có
- đầu tiên là góc A chung và góc abc bằng
- với góc ADB theo giả thiết như vậy tam
- giác ABC đồng dạng với tam giác ADB theo
- trường hợp góc góc đến đây ta suy ra
- ngay AB tr AD bằ AC tr AB gặp cạnh tương
- ứng và do đó áp dụng tính chất tỉ lệ
- thức ta được AB bình phương bằng AD nh
- AC Đây là điều phải chứng
- minh như vậy là ta đã hoàn thành hỏi
- trầm số 4 Bây giờ chúng ta hãy cùng nhau
- sang đến hỏi chấm số 5 về phần này chúng
- ta sẽ sử dụng trường hợp đồng dạng thứ
- ba của tam giác để chứng B một tính
- chất Chứng minh rằng nếu tam giác a'b'c'
- đồng dạng với tam giác abc theo tỉ số
- k và am a' m' lần lượt là các đường phân
- giác của tam giác ABC và tam giác
- a'b'c' thì a' m' tr AM bằng k bằng tỷ số
- đồng
- dạng định lý này nói rằng nếu như hai
- tam giác đồng dạng theo tỷ số
- k thì tỷ số giữa hai đường phân giác
- tương ứng với các đỉnh cũng sẽ bằng tỷ
- số
- k về hướng làm của bài này để chứng minh
- K = a' m' tr am thì chúng ta cần phải
- đưa tỷ số đồng dạng K về tỉ số hai cạnh
- cụ thể tương
- ứng ở đây thầy sẽ chọn hai cạnh đó là
- cạnh a'b' và cạnh
- AB như vậy ta cần phải chứng minh a' m'
- tr am bằ a'b' tr
- AB và bây giờ chúng ta sẽ phải chọn ra
- hai tam giác đồng dạng để suy ra tỉ số
- này cụ thể hơn ta cần phải chứng minh
- tam giác ABM đồng dạng với tam giác a'b'
- m' để chứng minh được điều này chúng ta
- sẽ sử dụng giả thiết tam giác a'b'c'
- đồng dạng V tam giác ABC ta suy
- ra trước hết là góc B bằng với góc
- b' góc Bac sẽ bằng với góc
- b'c
- Mặt khác do am là tê phân giác Của bac
- nên ta suy ra ngay góc bam sẽ bằng một
- nửa góc
- Bac tương tự với a' m' là tiê phân giác
- của góc b'
- a'c' nên b'' m' sẽ bằng 1/2 góc b'
- a'c' từ ba điều
- này ta suy ra góc bam bằng với góc b' a'
- m' như vậy là ta đã chỉ ra được hai cặp
- góc tương ứng bằng nhau ở hai tam giác
- cần chứng minh đó là góc B bằng với góc
- b' và góc bam bằng với góc b''
- m' như vậy tam giác a'b' m' đồng dạng
- với tam giác ABM theo trường hợp góc góc
- và từ đây ta suy ra a' m' tr am = a'b'
- tr AB cặp cạnh tương ứng mà a'b' tr AB
- lại bằng tỉ số đồng dạng K do đó tỉ số
- giữa hai đường phân giác a' m' trên AM
- bằng với tỉ số đồng dạng ta có điều phải
- chứng
- minh và đây cũng là bài tập cuối cùng
- thầy mang đến cho các em ở trong phần
- này
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây