Bài học cùng chủ đề
- Trường hợp đồng dạng thứ nhất của tam giác (c.c.c)
- Trường hợp đồng dạng thứ nhất của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ nhất của hai tam giác (vận dụng)
- Trường hợp đồng dạng thứ hai của tam giác (c.g.c)
- Trường hợp đồng dạng thứ hai của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ hai của hai tam giác (vận dụng)
- Trường hợp đồng dạng thứ ba của tam giác (g.g)
- Trường hợp đồng dạng thứ ba của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ ba của hai tam giác (nâng cao)
- Trường hợp bằng nhau thứ nhất của hai tam giác
- Trường hợp bằng nhau thứ hai của hai tam giác
- Trường hợp bằng nhau thứ ba của hai tam giác
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Trường hợp bằng nhau thứ hai của hai tam giác SVIP
Trường hợp đồng dạng thứ hai của tam giác (c.g.c)
1. Định lí

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
Ví dụ 1. Chứng minh tam giác $ABC$ đồng dạng với tam giác $IHG$.
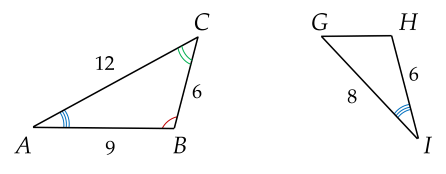
Lời giải
$\dfrac{AB}{IH}=\dfrac{9}{6}=\dfrac{3}{2}$;
$\dfrac{AC}{IG}=\dfrac{12}{8}=\dfrac{3}{2}$.
Xét tam giác $ABC$ và tam giác $IHG$ có:
$\widehat{A}=\widehat{I}$;
$\dfrac{A B}{I H}=\dfrac{A C}{I G}$
Suy ra $\Delta A B C \backsim \Delta IH G$ (c.g.c).
2. Ứng dụng
Ví dụ 2. Sử dụng trường hợp cạnh - góc - cạnh, chứng minh: Tỉ số hai đường trung tuyến tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.

Lời giải
Vì $\Delta A B C \backsim \Delta D E F$ nên
$\widehat{B}=\widehat{E}$
$\dfrac{A B}{D E}=\dfrac{B C}{E F}=\dfrac{B C \, : \, 2}{E F \, : \, 2}=\dfrac{M B}{E N}$.
Xét tam giác $\Delta A B M$ và $\Delta D E N$ có:
$\widehat{B}=\widehat{E}$;
$\dfrac{A B}{D E}=\dfrac{M B}{E N}$
Suy ra $\Delta A B M \backsim \Delta D E N$ (c.g.c).
Suy ra $\dfrac{A B}{D E}=\dfrac{A M}{D N}=k$.

Bạn có thể đánh giá bài học này ở đây