Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Quy tắc ba điểm: Với ba điểm bất kì $A, B, C$, ta có $\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}$.
Quy tắc hình bình hành: Nếu $A B C D$ là một hình bình hành thì $\overrightarrow{A B}+\overrightarrow{A D}=\overrightarrow{A C}$.
Với ba vectơ $\vec{a}, \vec{b}, \vec{c}$ tuỳ $\dot{y}$ :
- Tính chất giao hoán: $\vec{a}+\vec{b}=\vec{b}+\vec{a}$;
- Tính chất kết hợp: $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$;
- Tính chất của vectơ-không: $\vec{a}+\overrightarrow{0}=\overrightarrow{0}+\vec{a}=\vec{a}$.
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Điền kí hiệu thích hợp vào ô trống.
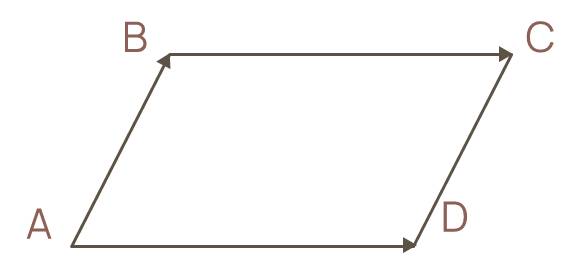
AB+AD=AB+ = .
BD ADBCAC
(Kéo thả hoặc click vào để điền)
Câu 2 (1đ):
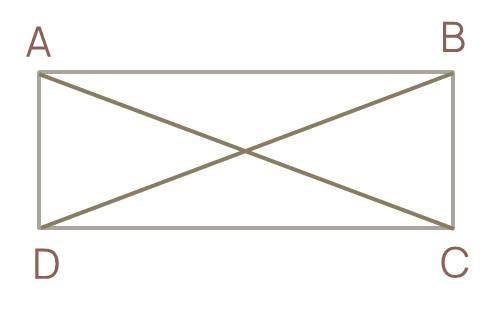
Cho hình chữ nhật ABCD.
AB+AD= ;
BA+BC= .
CA DBBD AC
(Kéo thả hoặc click vào để điền)
Câu 3 (1đ):
AB+CD+BC=
=AB+ +
= +CD
= AD.
CDBCAC
(Kéo thả hoặc click vào để điền)
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- ừ ừ
- Xin chào mừng các em đã quay trở lại với
- khoa toán lớp 10 của trường webtruyen.vn
- ở bạc trước chúng ta được làm quen với
- vectơ Hôm nay chúng ta sẽ bắt đầu tìm
- hiểu các phép toán có liên quan đến
- vector bác gồm các phép cộng phép trừ và
- phép nhân vectơ với một số
- Ừ bác này ta sẽ tìm hiểu về tổng và hiệu
- của Vectơ để mở đầu trong bài hôm nay
- thì chúng ta sẽ cùng tìm hiểu một vài
- tình huống thực tế mà chúng ta sẽ áp
- dụng các bạn phải lên converter các em
- hãy chú ý vào hình vẽ thể đưa ra đây
- chúng ta có thể thấy tình huống này
- trong thực tế đó là hai vật kéo một vật
- hai chiếc thuyền nhỏ kéo hai chiếc
- thuyền nhỏ kéo về 2 hướng khác nhau
- nhưng chiếc thuyền lớn lại di chuyển
- theo một hướng cố định ở đây chúng ta có
- thể hiểu chuyển động của chiếc thuyền ở
- trên được biểu diễn bằng vectơ này con
- chuyển động của trên thế giới biểu diễn
- theo vectơ này Thế còn chuyển động của
- chiếc thuyền lớn đều biểu diễn thể thơ
- này
- ở một tỉnh khác
- chiếc canô di chuyển ở trên một dòng
- sông chuyển động của chiếc canô so với
- mặt nước được biểu thị bằng vectơ màu đỏ
- so với mặt nước thì sẽ cắt nó sẽ di
- chuyển vuông góc tức là chiếc ca nô được
- đánh lái thật từ bên này sang bờ bên kia
- sự chuyển động của dòng nước để biểu thị
- bằng vectơ màu xanh Vậy thì các em cũng
- có thể hình dung ra ngay
- ở đó là gì chiếc cano này nó sẽ bị đi
- lệch về hướng bên phải chứ đó sẽ không
- đi thẳng theo hướng lái của người lại
- cano đây cũng là một tình huống liên
- quan đến các phép toán vectơ Chúng ta sẽ
- cùng tìm hiểu kỹ trong bạc ngày hôm nay
- đầu tiên ta sẽ cùng tìm hiểu về tổng của
- hai vectơ
- thấy có hai vectơ a và b
- Vậy thì tổng của hai vectơ a và b sẽ
- được định nghĩa như thế nào
- trên mặt phẳng thấy lấy một điểm A tùy ý
- Ừ từ điểm A thấy xây dựng vectơ AB hai
- vectơ có điểm đầu là a và điểm cuối là B
- như bài trước ta đã học là sẽ luôn tìm
- được 1 điểm B duy nhất thảm án vectơ AB
- bằng vectơ A và từ điểm B Thấy dựng
- vectơ BC
- = CE từ B điểm C cũng được xác định duy
- nhất
- và vectơ AC sẽ được gọi là tổng của hai
- vectơ A và B
- chúng ta ký hiệu là vectơ a dấu cộng các
- từ B như thế này
- và ta cần phải biết vectơ a + vectơ B
- bằng vectơ AC thì thế này đây là định
- nghĩa về tổng vectơ phải đi trong thực
- tế Chúng ta sẽ tìm tổng hòa các tư thế
- nào ta sẽ vận dụng một vài quy tắc như
- sau
- khi chúng ta sẽ có hai quy tắc để tính
- tổng hai vectơ đó là quy tắc 3 điểm và
- quy tắc hình bình hành
- các quy tắc 3 điểm là được sinh ra trực
- tiếp từ định nghĩa tổng quát vector tức
- là gì chúng ta có ba điểm A B C bất kỳ
- thì ta luôn có
- a vectơ AB + vectơ BC = vectơ AC nó
- chính là điểm đầu của thứ hai thì khi
- cổng vào nhau ta tưởng tượng nó triệt
- tiêu cho nào thì còn lại a và c chúng ta
- cũng có thể tưởng tượng này nếu tán đi
- một con đường từ A đến B
- Ừ rồi lại đi từ B đến C thì cũng giống
- như là ta đi từ A đến C
- các quy tắc thứ hai là quy tắc 7 ngày
- Ừ thì tao có hình bình hành ABCD Ở đây
- bây giờ kem hay tìm được giải tổng hai
- vectơ a b và AD
- em dựa vào quy tắc 3 điểm
- Ừ thì ta thấy ta chưa áp dụng ngay thì
- tao bảo mày được bởi vì
- ta phải có một bước đến rồi ở đó là gì
- ad thì thấy sẽ viết nó bằng cách tớ PC
- như vậy thì sẽ = AB
- a + b c
- ở đây tác dụng với ta điểm vào ta được
- là bằng vectơ
- ê ê ê ê
- Ừ như vậy trong hình bình hành ABCD
- ta có vectơ AB + vectơ AD = vectơ AC
- các quy tắc này cũng rất là trực quan và
- dễ nhớ chúng ta có thể nhớ là bắt đầu
- xuất phát từ một đỉnh của những hàng lấy
- là điểm ngốc thì tổng của hai vectơ có
- giá là hai cạnh sẽ là vectơ có giá là
- đường chéo Đây là hai quy tắc chúng tác
- dụng để tìm tổng hai vectơ quy tắc 3
- điểm và quy tắc hình bình hành
- ạ Bây giờ các em hãy áp dụng các quy tắc
- này để làm sao Thế có hình chữ nhật ABCD
- theo cái chứng minh cho thầy độ dài của
- Tổng 24 AB và AD sẽ bằng độ dài của tổng
- hai vectơ ba = BC
- ở đây chúng ta hiểu là gì hai vectơ AB
- và D cộng với nhau Nó sẽ ra một vectơ a
- nào đó
- cho hai vectơ B A và B C tổng của nó
- cũng là 15-cb đó thì chúng ta lấy độ dài
- và nghe rõ này à
- số Viettel chúng ta chứng minh độ dài
- của hai vectơ bằng nhau chắc chắn là
- chúng ta phải tìm xem là tổng hai vectơ
- AB AD là gì và tổng hai vectơ B A B C là
- gì ab + ad
- thì áp dụng ngay quy tắc thì bình hành
- ra thấy ngày nó bằng vectơ AC Thế còn b
- a + b c nó sẽ bằng vectơ BD
- anh cũng theo quy tắc hình
- Khi mà ta có độ dài của vectơ AC nó sẽ
- bằng độ dài của đoạn thẳng ac độ dài
- đoạn thẳng ac sẽ bằng độ dài của thẳng
- BD bởi vì đây là hai đường chéo của một
- hình chữ nhật
- chế độ dài đoạn thẳng BD là không chính
- là độ dài của Vectơ BD Vậy thì sẽ có
- đẳng thức mà bảo hiểm của Chứng minh
- phép cộng 24 nó cũng có một số tính chất
- mà chúng ta đã quen thuộc với phép cộng
- các số đầu tiên đó là tính chất giao
- hoán Nếu chúng ta đổi chỗ các vector ở
- trong một tổng thi tổng nhận được không
- thay đổi được hình ảnh vectơ a + vectơ B
- bằng vectơ B của thứ hai
- số thứ tự nó không làm ảnh hưởng đến kết
- quả cuối cùng
- có tính chất kết hợp tức là tổng của
- Vectơ A và vectơ B cộng với c nó cũng
- bằng vectơ A + với tổng của vectơ B và C
- và cộng và các thực không thì các em
- cũng thể hình dung ra ngay là vectơ a +
- vectơ không nó sẽ bằng chính thứ hai
- bây giờ áp dụng các tính chất này chúng
- ta hãy cùng làm sao cho bốn điểm ABCD
- chứng minh đẳng thức vectơ AB + vectơ CD
- + vectơ BC = vectơ AD thông thường khi
- cho tổng của các vector mà không gắn với
- một hình vẽ cụ thể như là hình bình hành
- hay là hình chữ nhật thì chúng ta sẽ áp
- dụng quy tắc 3 điểm để thực hiện phép
- cộng Hamster Thế thì để áp dụng quy tắc
- 3 điểm khách quan sát về bên trái chúng
- ta cần phải làm gì chúng ta cần phải đổi
- chỗ vectơ BC và phím c d để chúng ta sẽ
- có lá để bên trái sẽ bằng vectơ AB chúng
- ta giữ nguyên vị trí đổi vị trí của
- Vectơ BC lên ở đây chúng ta đã áp dụng
- tính chất Giao hoán
- em đổi chỗ các vectơ trong một tập thi
- sẽ không làm ảnh hưởng đến tổng nhận
- được vectơ AB + vectơ BC áp dụng quy tắc
- 3 điểm giành được bằng vectơ AC đến đây
- là áp dụng tiếp khi ta điểm chúng ta có
- bản vectơ ad
- ạ Bây giờ chúng ta lấy bốn điểm bất kì
- trên mặt với bên trái này sẽ bằng gì AB
- e + CD
- a + b c
- thì chúng ta thấy ngay nó là AB + BC +
- CD thì nó sẽ bằng
- nó sẽ mặt a d
OLMc◯2022


Bạn có thể đánh giá bài học này ở đây