Bài học cùng chủ đề
- Định nghĩa và tính chất
- Tính chất trung điểm, trọng tâm. Điều kiện để hai vectơ cùng phương
- Phân tích một vectơ theo hai vectơ không cùng phương
- Độ dài biểu thức vectơ. Phân tích vectơ
- Đẳng thức vectơ
- Tìm điểm thỏa mãn đẳng thức vectơ
- Luyện tập tổng hợp
- Bài tập tự luận: Phân tích một vectơ theo hai vectơ không cùng phương, tìm điểm thỏa mãn hệ thức vectơ
- Bài tập tự luận: Chứng minh đẳng thức vectơ. Chứng minh ba điểm thẳng hàng
- Phiếu bài tập: Tích của vectơ với một số
- Tích của một số với một vectơ
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tính chất trung điểm, trọng tâm. Điều kiện để hai vectơ cùng phương SVIP

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
- Nếu $I$ là trung điểm của đoạn thẳng $A B$ thì $\overrightarrow{M A}+\overrightarrow{M B}=2 \overrightarrow{M I}$ với điểm $M$ bất kì.
- Nếu $G$ là trọng tâm của tam giác $A B C$ thì $\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}=3 \overrightarrow{M G}$ vối điểm $M$ bất kì.
- Điều kiện cần và đủ để hai vectơ $\vec{a}$ và $\vec{b}(\vec{b} \neq \overrightarrow{0})$ cùng phương là có một số thực $k$ để $\vec{a}=k \vec{b}$.
- Điều kiện cần và đủ để ba điểm phân biệt $A, B, C$ thẳng hàng là có số thực $k$ để $\overrightarrow{A B}=k \overrightarrow{A C}$
Điền kí hiệu thích hợp vào ô trống.
MA=MI+ ;
MB= + ;
(Kéo thả hoặc click vào để điền)
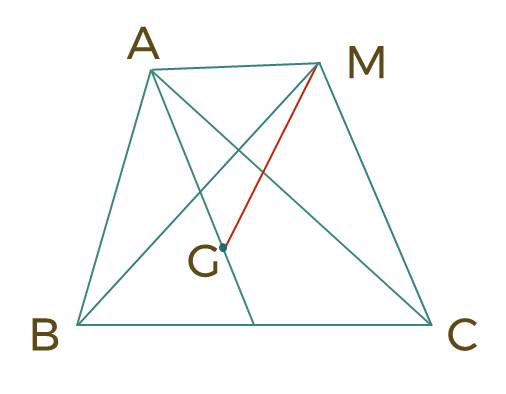
Tam giác ABC có trọng tâm G. Ta có: MA+MB+MC= .MG.
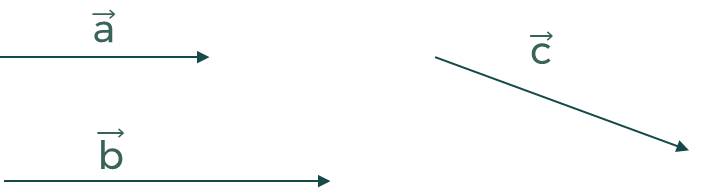
Cho a=2;b=3.
Ta có a= .b.
(Kéo thả hoặc click vào để điền)

Cho a=2;c=3.
Mỗi khẳng định sau đúng hay sai?
(Nhấp vào dòng để chọn đúng / sai)| a=32c. |
|
| a=32c. |
|
Cho ba điểm phân biệt thẳng hàng A, B, C. Mỗi khẳng định sau đúng hay sai?
(Nhấp vào dòng để chọn đúng / sai)| AC=kBA. |
|
| BC=mCB. |
|
| CB=hBA. |
|
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Ừ
- từ việc định nghĩa được tích của Vectơ
- với một số thực thì chúng ta sẽ có những
- tính chất thì rất thú vị ở đây thầy sẽ
- giới thiệu cho chúng ta về các tính chất
- liên quan đến trung điểm của đoạn thẳng
- và trọng tâm lượng giác
- Em thấy có đoạn thẳng AB B I I là trung
- điểm của cạnh AB và một điểm M bất kì
- khi các sẽ luôn có đẳng thức vectơ ma
- a + vectơ MB
- thì nó sẽ có liên hệ gì với vectơ My
- Anh ta sẽ điểm của con số nhân với vectơ
- bởi vào đây các thử tìm xem đó phần nào
- khi áp dụng bài trước là bài tổng và
- hiệu hai vectơ chúng ta cũng có thể tìm
- một con số này
- ở đó là các xây dựng hình bình hành mà
- có hai cạnh kề nhau là ma và MB sử dụng
- đặc điểm tình hình đây
- Cách thứ hai mà ta rất hay sử dụng trong
- các bài toán chứng minh đẳng thức hay là
- tìm điểm sau này vectơ và ta sẽ trang
- điểm ở đây ta xem là ma + Mb bằng bao
- nhiêu lần nội y thì thấy sẽ chen điểm y
- vào để xuất hiện mới khi trở lại đi vào
- thì Ma thầy sẽ viết thành
- Ừ vợ yêu à
- I + II ra à
- a MB này sẽ thành My
- e + ib
- khi đến đây có em hãy thảm họa và nhóm
- các vector này một cách phù hợp bơ y thì
- sẽ ghép với nội y thì trai sẽ được là
- hai mới đi
- số còn lại là í a
- A Gọi B
- Em hãy cho điện thoại như thế này thì ta
- thấy ngay là ia + ib nó bằng không bảo
- vệ được không
- chú vịt yêu 7B là 24 đối nhau ngược
- hướng và cùng độ dài
- Ừ như vậy Kết quả nhận được cuối cùng sẽ
- là hai lần mấy
- đàn tính chất cực kỳ quan trọng ta rất
- nhiều cho con này Thắng decker cái này
- khi nhớ đến chỗ này nhá
- tính chất thứ hai liên quan đến trọng
- tâm của tam giác thì có tam giác ABC G
- là trọng tâm của tam giác này Vậy thì ta
- sẽ có hệ thức là be + MB
- + MC
- vẽ M là một điểm bất kì nó sẽ có liên hệ
- với mg
- Anh ta sẽ điểm của con số gần đây các
- con số nào áp dụng tương tự như bài trên
- chúng ta sẽ trang điểm G và ta sẽ phân
- tích m a = m g g tương tự với MB = MC
- thì ta sẽ tìm được con số để gọi này nó
- số 3A
- cho ma + mb + MC = 3 Mg
- kem đây có thể mở rộng ra với một đa
- giác n cạnh và có điểm G là trọng tâm
- của tam giác đỏ trọng tâm của ra thì
- thấy cũng giới thiệu về trước rồi
- vì nó là điểm mà làm cho ga1
- + nửa 2
- + Vân Vân + đến cơ an ở
- anh sẽ bảo vệ được không vẽ 12 n nó lật
- các đỉnh của đa giác lồi n cạnh
- Ừ thì khi đó chúng ta cũng sẽ có là ma1
- e + M2
- khi cậu đến MN à
- thì nó sẽ bằng N lần Mg
- trường hợp tam giác hay thậm chí là
- trường hợp đoạn thẳng là cũng là thưởng
- đặc biệt của trường về thôi
- khi định nghĩa được tích của Vectơ với
- một số thì ta sẽ dễ dàng xét được hai
- Vectơ cùng phương với nhau hay không
- Điều kiện à bây giờ cùng phương là gì
- để hai ô tô A và B Trong và vectơ B khác
- được không cùng phương với nhau là có
- một số K để vectơ a = k nhân dân từ B
- điều kiện cần và đủ đây tức là gì Nếu A
- và B cùng Phương thì ta phải có số ca
- thỏa mãn khi thức này và ngược lại nếu
- ghép tựa vào bậc k những cái từ B A và B
- là hai việc cùng vuông ở
- ạ bây giờ cái mình quan sát ở đây Thành
- có 3 vectơ vectơ a vectơ B vectơ C thay
- cho độ dài của các vector này vectơ a độ
- dài bằng hai vectơ B độ dài bằng 3 và
- vectơ C độ dài cũ bằng 3A
- khi chúng ta thấy ngay là vectơ A và
- vectơ B Cùng phường với nhau cho nên là
- sẽ có một số ca thỏa mãn là a bằng KNB
- phải số ca Chúng ta sẽ tìm ra à Anh ở ví
- dụ đầu tiên của ngày hôm nay chúng ta
- cũng đã nắm được một cách cơ bản về cách
- làm rồi ta sẽ xem độ dài của Vectơ A và
- vectơ B là hệ gì với nhau
- vectơ a = k nhân vectơ B số ca này nó
- phải có mã là gì nó chính là độ dài của
- việc từ A
- trên độ dài của vectơ B và chúng ta cần
- thêm dấu cộng hay dấu trừ đường trước
- của con số này
- Ừ tùy thuộc vào hướng của cơ thể nào VTB
- ở đây vectơ a vectơ B cùng hướng cho nên
- là ta sẽ giữ nguyên dấu tức là dấu đền +
- ca làm gương
- Ô thế cái máy tính có thể cảm bao nhiêu
- các hạng đây sẽ bằng 2/3
- a letter a a bằng 2/3 vectơ B
- Ừ vậy thì nếu thầy viết như thế này
- cho HTC không có được làm bằng 3 vectơ A
- được bằng hai thì thấy có thể biết là
- vectơ a bằng 2/3 chiều C như thế này
- không
- khi chúng ta thấy ngay là chắc không
- được bên này bởi vì sao vectơ A và BTC
- không cùng hướng
- Ừ nếu chúng ta biết biểu thức này thì đã
- nhầm coi là vectơ A và vectơ C cùng
- phương rồi
- chúng ta sẽ có một kết quả thì sao 3
- điểm phân biệt a b c sẽ thẳng hàng khi
- và chỉ khi có số ca khác 0 sao cho vectơ
- AB = ca thì cái tiêu C ở đây thời chỉ
- biết minh họa là cách từ AB và cái tụt
- canxi thôi thế còn chúng ta có thể lấy
- bất kỳ một cặp vectơ nào mà hai điểm đầu
- và cuối của các tờ đó là 2 trong 3 điểm
- cho và cả 3 điểm đó phải xuất hiện ở
- trong hình thức này thì ví dụ như là
- thành có thể viết lại CB
- sẽ = k nhân với
- AC + tùy trong các bạn cụ thể mà chúng
- ta sẽ chọn cảnh tương là phù hợp a

Bạn có thể đánh giá bài học này ở đây