Tích của một số với một vectơ SVIP

I. ĐỊNH NGHĨA

Cho số thực \(k\) và vectơ \(\overrightarrow{a}\). Tích của số \(k\) với vectơ \(\overrightarrow{a}\) là một vectơ, kí hiệu là \(k\overrightarrow{a}\), được xác định như sau:

Cùng hướng với vectơ \(\overrightarrow{a}\) nếu \(k>0\), ngược hướng với vectơ \(\overrightarrow{a}\) nếu \(k< 0\);

Có độ dài bằng \(\left|k\right|\left|\overrightarrow{a}\right|\).

Quy ước: \(0\overrightarrow{a}=\overrightarrow{0},k\overrightarrow{0}=\overrightarrow{0}.\)

Phép lấy tích của một số với một vectơ gọi là phép nhân số với vectơ.

II. TÍNH CHẤT

Với hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) và hai số thực \(h,k\), ta luôn có:

• \(k\left(\overrightarrow{a}+\overrightarrow{b}\right)=k\overrightarrow{a}+k\overrightarrow{b};k\left(\overrightarrow{a}-\overrightarrow{b}\right)=k\overrightarrow{a}-k\overrightarrow{b}\)
• \(\left(h+k\right)\overrightarrow{a}=h\overrightarrow{a}+k\overrightarrow{a};\)
• \(h\left(k\overrightarrow{a}\right)=\left(hk\right)\overrightarrow{a};\)
• \(1\overrightarrow{a}=\overrightarrow{a};\left(-1\right)\overrightarrow{a}=-\overrightarrow{a}.\)

Nhận xét:  \(k\overrightarrow{a}=\overrightarrow{0}\) khi và chỉ khi \(k=0\) hoặc \(\overrightarrow{a}=\overrightarrow{0}.\)

III. MỘT SỐ ỨNG DỤNG

1. Trung điểm của đoạn thẳng

Nếu \(I\) là trung điểm của đoạn thẳng \(AB\) thì \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\) với điểm \(M\) bất kì.

2. Trọng tâm tam giác

Nếu \(G\) là trọng tâm của tam giác \(ABC\) thì \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\) với điểm \(M\) bất kì. 

3. Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng

• Điều kiện cần và đủ để hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\left(\overrightarrow{b}\ne\overrightarrow{0}\right)\) cùng phương là có một số \(k\) để \(\overrightarrow{a}=k\overrightarrow{b}.\) 
• Điều kiện cần và đủ để ba điểm phân biệt \(A,B,C\) thẳng hàng là có số thực \(k\) để \(\overrightarrow{AB}=k\overrightarrow{AC}\).

Nhận xét: Trong mặt phẳng, cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) không cùng phương. Với mỗi vectơ \(\overrightarrow{c}\) có duy nhất cặp số \(\left(x;y\right)\) thỏa mãn \(\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}.\)

Ví dụ: Cho tam giác \(ABC\), điểm \(M\) trên cạnh \(BC\) sao cho \(MB=2MC\). Hãy phân tích vectơ \(\overrightarrow{AM}\) theo hai vectơ \(\overrightarrow{u}=\overrightarrow{AB}\) và \(\overrightarrow{v}=\overrightarrow{AC.}\)

Giải

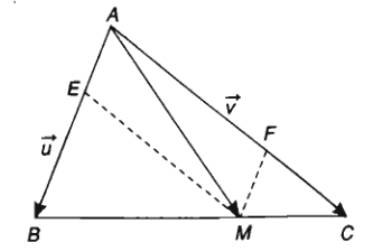
 Ta có

\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)

\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)

\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}.\)

\(=\dfrac{1}{3}\overrightarrow{u}+\dfrac{2}{3}\overrightarrow{v}.\)