Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

1. Hướng dẫn

$\sqrt{32}+\sqrt{50}-2 \sqrt{8}+\sqrt{18}$.

$ = \sqrt{16.2} + \sqrt{25.2} - \sqrt{16.2} + \sqrt{9.2}$

$ = 4\sqrt{2} + 5\sqrt{2} - 4\sqrt{2} + 3\sqrt{2}$

$ = (4+5-4+3)\sqrt{2} = 8\sqrt{2}$

2. Hướng dẫn

a) Điều kiện: $a>0$ và $a \neq 1$
$M =\Big(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}-1}\Big): \dfrac{\sqrt{a}+1}{a-2 \sqrt{a}+1}$

$=\Big(\dfrac{1}{\sqrt{a}(\sqrt{a}-1)}+\dfrac{1}{\sqrt{a}-1}\Big): \dfrac{\sqrt{a}+1}{(\sqrt{a}-1)^2}$ 

$=\dfrac{1+\sqrt{a}}{\sqrt{a}(\sqrt{a}-1)} \cdot \dfrac{(\sqrt{a}-1)^2}{\sqrt{a}+1}$

$=\dfrac{(1+\sqrt{a})(\sqrt{a}-1)^2}{\sqrt{a}(\sqrt{a}-1)(\sqrt{a}+1)}$

$=\dfrac{\sqrt{a}-1}{\sqrt{a}}$

b) Xét hiệu: 

$M-1=\dfrac{\sqrt{a}-1}{\sqrt{a}}-1=\dfrac{-1}{\sqrt{a}}<0$ với $a>0$ và $a \neq 1$.

Vậy $M<1$.

Hướng dẫn giải:

Gọi vận tốc thực của ca nô là $x$ $(x>5$; km/h$)$.

Vận tốc xuôi dòng của ca nô là $x+5$ km/h.

Vận tốc ngược dòng của ca nô là $x-5$ km/h.

Thời gian ca nô đi xuôi dòng là : $\dfrac{60}{x+5}$ (giờ)

Thời gian ca nô đi xuôi dòng là : $\dfrac{60}{x-5}$ (giờ)

Theo bài ra ta có phương trình:

$\dfrac{60}{x+5}+\dfrac{60}{x-5}=5$

$60(x-5)+60(x+5)=5\left(x^2-25\right)$

$5 x^2-120 x-125=0.$

Giải phương trình ta được: 

${x}_1=-1$ (không thỏa mãn điều kiện); 

${x}_2=25$ (thỏa mãn điều kiện)

Vậy vận tốc thực của ca nô là $25$ km/h.

Hướng dẫn giải:

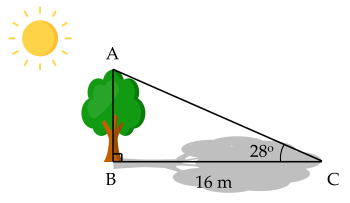
Gọi chiều cao của cây là $A B$, chiều dài của bóng cây là $B C$, góc tạo thành giữa tia nắng mặt trời với cây là $\widehat{C}$ và vị trí gốc cây là góc $\widehat{B}$.

Do cây thì luôn vuông góc với mặt đất nên ta có $\Delta A B C$ vuông tại $B$. Do đó ta có:

$\tan \widehat{C} = \dfrac{AB}{BC}$

Thay số, ta tính được

$A B=B C . \tan \widehat{C} =\tan 28^{\circ} . 16 \approx 8,5$ m.

Vậy cây cao khoảng $8,5$ m.

Hướng dẫn giải:

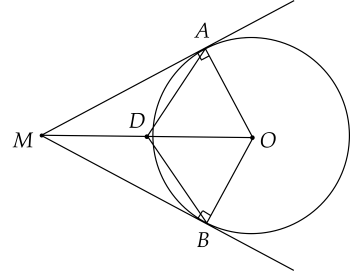
a) Gọi $D$ là trung điểm $MO.$

Xét tam giác $AMO$ vuông tại $A$, với $AD$ là đường trung tuyến ứng với cạnh huyền $MO$ của tam giác, suy ra $AD = DM = DO$ (1).

Xét tam giác $BMO$ vuông tại $A$, với $BD$ là đường trung tuyến ứng với cạnh huyền $MO$ của tam giác, suy ra $DO = DM = BD$ (2).

Từ (1) và (2) ta suy ra $DA = DM = DO = DB$. Vậy bốn điểm $A;M;B;O$ thuộc cùng một đường tròn.

b) Vì $A M$ và $B M$ là hai tiếp tuyến cắt nhau tại $M$

Suy ra $OM$ là tia phân giác của $\widehat{A M B}$ (tính chất hai tiếp tuyến cắt nhau).

Suy ra $\widehat{A M O}=\widehat{B M O}=\dfrac{\widehat{A M B} }{2}=\dfrac{40^{\circ}}{2} = 20^{\circ}$

Vì $AM$ là tiếp tuyến của đường tròn 

Suy ra $O A \perp A M$ (tính chất)

Suy ra $\widehat{O A M}=90^{\circ}$.

Xét tam giác $AOM$ có:

$\widehat{O A M}+\widehat{A M O}+\widehat{A O M}=180^{\circ}$ (định lí tổng ba góc của một tam giác)

$90^{\circ}+20^{\circ}+\widehat{A O M}=180^{\circ}$

$\widehat{A O M}=180^{\circ}-90^{\circ}-20^{\circ}$

$\widehat{A O M}=70^{\circ}$

c) Vì $AM$ và $BM$ là hai tiếp tuyến cắt nhau tại M.

$OM$ là tia phân giác $\widehat{A O B}$ (tính chất).

$\widehat{A O M}=\widehat{B O M}=\dfrac{\widehat{A O B}}{2}$

$\widehat{A O B}=2 \widehat{A O M}$

Suy ra $\widehat{A O B}=2.70^{\circ}=140^{\circ}$

Ta có: $\widehat{A O B}$ là góc ở tâm chắn cung nhỏ $\stackrel\frown{A B}$

Vậy số đo góc $AOB$ bằng số đo cung nhỏ $AB$ (định lí góc ở tâm).

số đo cung ${A B}$ nhỏ là $=140^{\circ}$

Số đo cung ${A B}$ lớn là:

$360^{\circ}$ - sđ $\stackrel\frown{A B}$ nhỏ

$=360^{\circ}-140^{\circ}=220^{\circ}$

Hướng dẫn giải:

$x - 3\sqrt{x} + 2 < 0$

Điều kiện: $x \geq 0$.

$(\sqrt{x}-1) (\sqrt{x}-2) < 0$.

Ta xét hai trường hợp:

- Trường hợp 1:

$\sqrt{x}-1 < 0$ và $\sqrt{x} -2 > 0$

$\sqrt{x} < 1$ và $\sqrt{x}  > 2$

$x < 1$ và ${x}  > 4$ (vô lí)

- Trường hợp 2:

$\sqrt{x} - 1 > 0$ và $\sqrt{x} - 2 < 0$

$\sqrt{x} > 1$ và $\sqrt{x} < 2$

${x} > 1$ và ${x} < 4$

Kết hợp với điều kiện xác định là $x \geq 0$, ta có: $1 < x < 4$.