Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
Bài 1. (2,5 điểm)
1) Rút gọn các biểu thức sau:
$A=10\sqrt{\dfrac{1}{5}}-3 \sqrt{(2-\sqrt{5})^2}+\sqrt{5}$.
$B=\left(\dfrac{4 \sqrt{x}}{\sqrt{x}+2}-\dfrac{8 x}{x-4}\right):\left(\dfrac{\sqrt{x}-1}{x-2 \sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)$ với $x>0 ; x \neq 4 \text {. }$
2) Tìm $x$ biết $\sqrt{4 x^2-4 x+1}=\sqrt[3]{27}$.
Hướng dẫn giải:
1) $A=10 \sqrt{\dfrac{1}{5}}-3 \sqrt{(2-\sqrt{5})^2}+\sqrt{5}$
$=2 \sqrt{5}-3|2-\sqrt{5}|+\sqrt{5}=2 \sqrt{5}-3(\sqrt{5}-2)+\sqrt{5}$
$=2 \sqrt{5}-3 \sqrt{5}+6+\sqrt{5}=6$
Với $x>0 ; x \neq 4$ ta có
$B=\left(\dfrac{4 \sqrt{x}}{\sqrt{x}+2}-\dfrac{8 x}{x-4}\right):\left(\dfrac{\sqrt{x}-1}{x-2 \sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)$
$=\left[\dfrac{4 \sqrt{x}}{\sqrt{x}+2}-\dfrac{8 x}{(\sqrt{x}+2)(\sqrt{x}-2)}\right]:\left[\dfrac{\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-2)}-\dfrac{2}{\sqrt{x}}\right]$
$=\dfrac{4 \sqrt{x}(\sqrt{x}-2)-8 x}{(\sqrt{x}+2)(\sqrt{x}-2)}: \dfrac{\sqrt{x}-1-2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}$
$=\dfrac{4 x-8 \sqrt{x}-8 x}{(\sqrt{x}+2)(\sqrt{x}-2)}: \dfrac{\sqrt{x}-1-2 \sqrt{x}+4}{\sqrt{x}(\sqrt{x}-2)}$
$=\dfrac{-4 x-8 \sqrt{x}}{(\sqrt{x}+2)(\sqrt{x}-2)}: \dfrac{-\sqrt{x}+3}{\sqrt{x}(\sqrt{x}-2)}$
$=\dfrac{-4 \sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}+2)(\sqrt{x}-2)} \cdot \dfrac{\sqrt{x}(\sqrt{x}-2)}{-\sqrt{x}+3}$
$=\dfrac{4 x}{\sqrt{x}-3}$
2) $\sqrt{4 x^2-4 x+1}=\sqrt[3]{27} \Leftrightarrow \sqrt{(2 x-1)^2}=3$
$\Leftrightarrow |2 x-1|=3$
$\Leftrightarrow \left[\begin{aligned}& 2x-1=3 \\& 2x-1=-3 \end{aligned}\right.$.
$\Leftrightarrow \left[\begin{aligned}& 2x=4 \\& 2x=-2 \end{aligned}\right.$.
$\Leftrightarrow \left[\begin{aligned}& x=2 \\& x=-1 \end{aligned}\right.$.
Vậy $x=2,\,x=-1$.
Bài 2. ($1,5$ điểm) Cho hàm số $y=(m-2) x+m+3$ (1) (với $m$ là tham số và $m \neq 2$ ).
1) Vẽ đồ thị hàm số (1) với $m=1$.
2) Xác định giá trị của ${m}$ để đồ thị hàm số (1) cắt đường thẳng $y=5 x-1$ tại một điểm trên trục tung.
Hướng dẫn giải:
1) Với $m=1$ hàm số (1) trở thành $y=-x+4$.
Với $x=0 \Rightarrow y=4$ ta có điểm $(0 ; 4)$ thuộc trục ${Oy}$.
Với $y=0 \Rightarrow x=4$ ta có điểm $(4 ; 0)$ thuộc trục ${Ox}$.
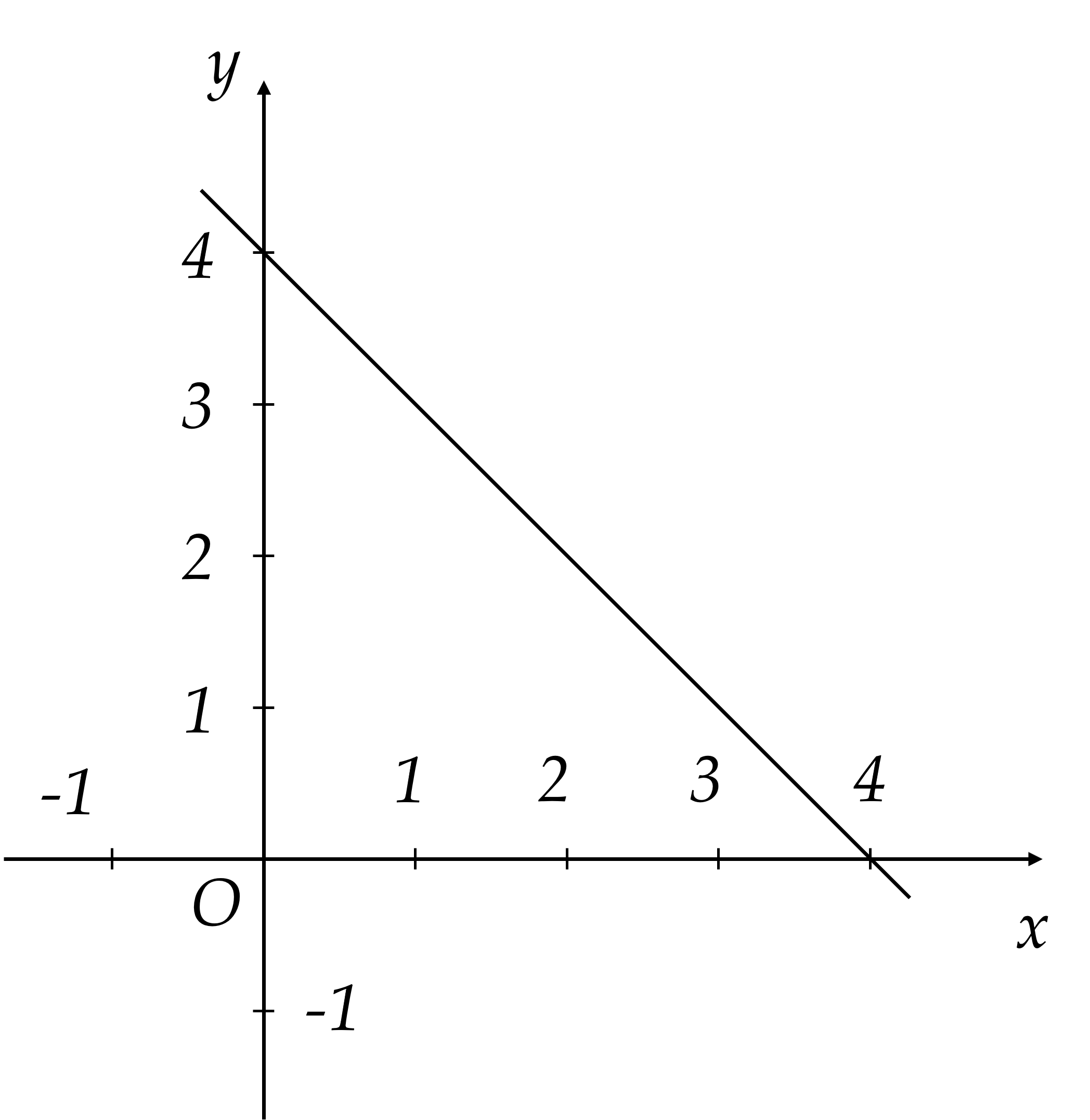
Đồ thị hàm số $y=-x+4$ là đường thẳng đi qua hai điểm $(0 ; 4)$ và $(4 ; 0)$.
2) Đồ thị hàm số (1) cắt đường thẳng $y=5 x-1$ khi và chỉ khi $m-2 \neq 5 \Leftrightarrow m \neq 7$
Với $m \neq 2$ hàm số $y=(m-2) x+m+3$ là hàm số bậc nhất.
Đồ thị hàm số (1) cắt đường thẳng $y=5 x-1$ tại 1 điểm trên trục tung.
$\Leftrightarrow m+3=-1$
$\Leftrightarrow m=-4$ (thoả mãn $m \neq 7$ và $m \neq 2$ )
Vậy $m=-4$.
Bài 3.
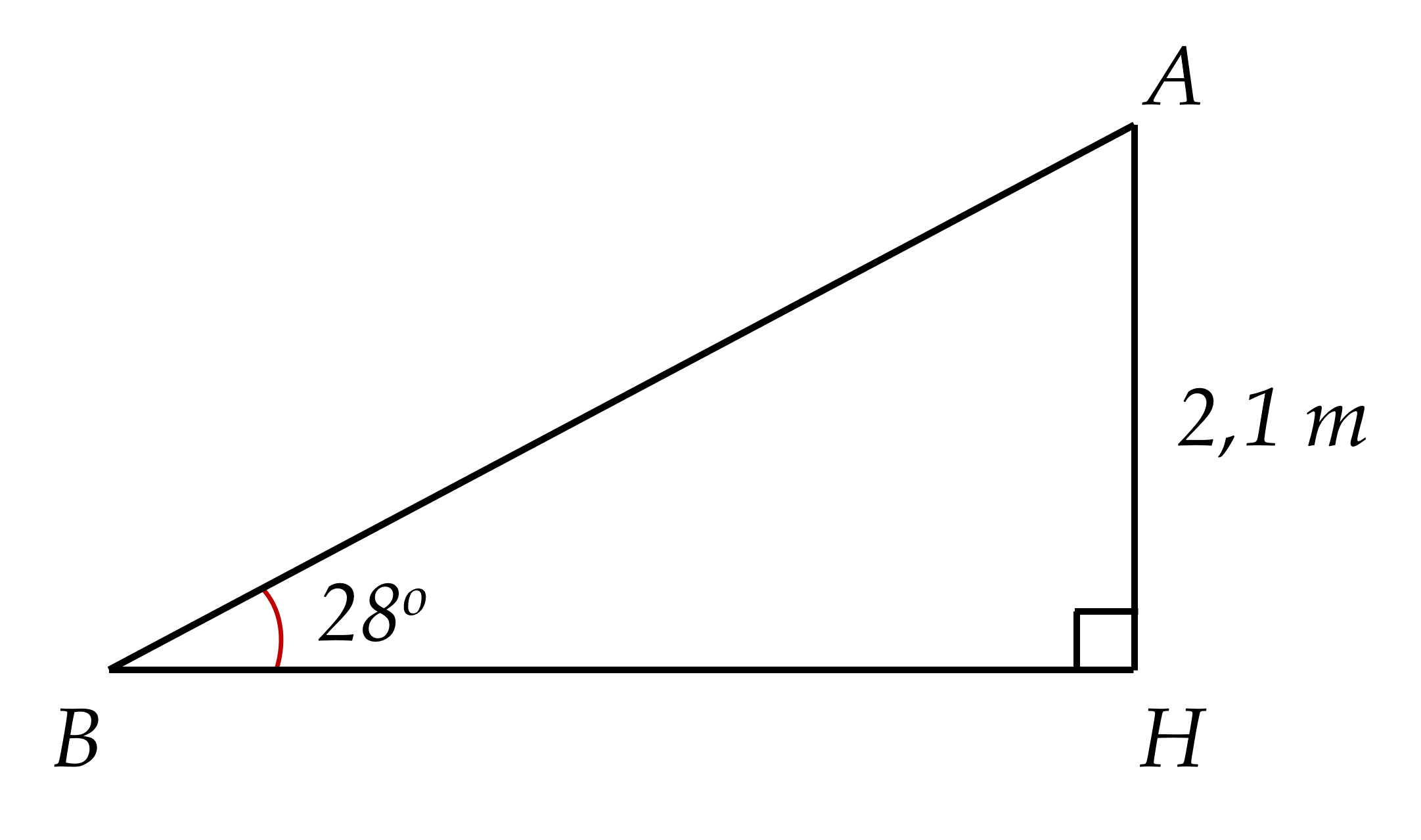
1) Một cầu trượt trong công viên có độ dốc so với mặt đất là $28^{\circ}$ và độ cao là $2,1$ m (được biểu diễn ở hình vẽ). Tính độ dài của mặt cầu trượt (kết quả làm tròn đến chữ số thập phân thứ nhất).
2) Cho đường tròn $(O ; R)$, đường kính $A B . M$ là điểm nằm trên đường tròn $(O ; R)$ và $A M<B M$ ( $M$ khác $A)$. Vẽ $O H$ vuông góc với $B M$ tại $H$. Tiếp tuyến tại $B$ của đường tròn $(O ; R)$ cắt $O H$ tại $N$.
a) Chứng minh $H$ là trung điểm của $B M$ và $M N$ là tiếp tuyến của đường tròn $(O ; R)$.
b) Gọi $K$ là trung điểm của $H N$. Gọi $I$ là giao điểm của $B K$ với $(O ; R)$. Chứng minh $\triangle M A B$ đồng dạng $\triangle H B N$ và ba điểm $A, H, I$ thẳng hàng.
Hướng dẫn giải:
1) Xét $\triangle A H B$ vuông tại ${H}$.
Có $\sin \widehat{A B H}=\dfrac{A H}{A B}$.
$\Rightarrow A B=\dfrac{A H}{\sin \widehat{A B H}}$.
$\Rightarrow A B=\dfrac{2,1}{\sin 28^{\circ}} \approx 4,5(\mathrm{~m})$
Vậy độ dài của mặt cầu trượt xấp xỉ $4,5$ m.
2)
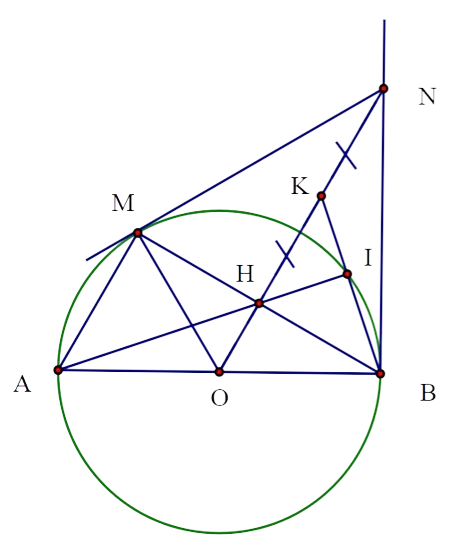
a) Ta có $\triangle B O M$ cân tại ${O}( {OB}= {OM}= {R})$
Mà $O H \perp B M$ hay $ {OH}$ là đường cao của $\triangle B O M$
$\Rightarrow {OH}$ là đường trung tuyến, là đường trung trực của $\triangle B O M$
$\Rightarrow {H}$ trung điểm của ${MB}$.
Chứng minh: $\triangle B O N=\triangle M O N$ (c.c.c)
$\Rightarrow \widehat{N M O}=\widehat{N B O}=90^{\circ} \Rightarrow {MN}$ là tiếp tuyến của $({O}, {R})$.
b) *) Chứng minh được $\triangle M A B$ đồng dạng $\triangle H B N$ (g.g)
*) và ba điểm $A, H, I$ thẳng hàng
$\triangle M A B \sim \triangle H B N \Rightarrow \dfrac{M B}{H N}=\dfrac{A B}{B N} \Rightarrow \dfrac{A B}{B N}=\dfrac{2 H B}{2 K N}=\dfrac{H B}{K N}$
Chứng minh được: $\triangle H A B \sim \triangle K B N$ (c.g.c) $\Rightarrow \widehat{H A B}=\widehat{K B N}$
Chứng minh được $\triangle A B I$ vuông tại ${I} \Rightarrow \widehat{I A B}=\widehat{K B N}$ (cùng phụ với $\widehat{I B A}$ $\Rightarrow \widehat{H A B}=\widehat{I A B}$, mà $ {H}$, I cùng thuộc nửa mặt phẳng bờ $ {AB}$ nên tia $A I$ trùng với tia $A H$ hay 3 điểm $ {A}, {H}, {I}$ thẳng hàng.
Bài 4. (1,0 điểm)
Giải phương trình $\sqrt{x+3} . x^4=2 x^4-2023 x+2023$.
Hướng dẫn giải:
ĐKXĐ: $x \geq-3$
$\sqrt{x+3} . x^4=2 x^4-2023 x+2023$
$\Leftrightarrow x^4(\sqrt{x+3}-2)+2023(x-1)=0$
$\Leftrightarrow \dfrac{x^4(x-1)}{\sqrt{x+3}+2}+2023(x-1)=0$
$\Leftrightarrow(x-1)\left(\dfrac{x^4}{\sqrt{x+3}+2}+2023\right)=0$
$\Leftrightarrow x-1=0$
$\Leftrightarrow x=1(t / m)$
$\left(\text { Vì } \dfrac{x^4}{\sqrt{x+3}+2}+2023>0\right).$
