Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Ôn tập: Chứng minh đường thẳng song song với mặt phẳng SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
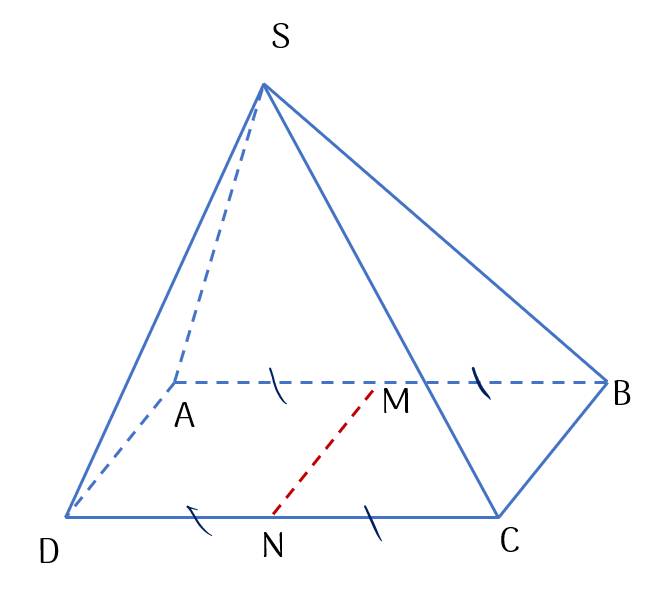
MN song song với đường thẳng mặt phẳng (SAD).
MN song song với đường thẳng mặt phẳng (SBC).
SASCADBCSBSD
(Kéo thả hoặc click vào để điền)
Câu 2 (1đ):
Câu hỏi có thể có nhiều đáp án đúng.
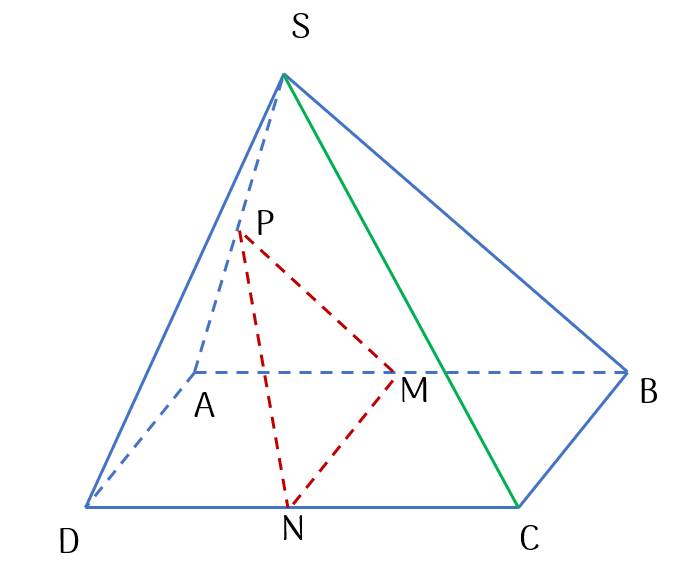
Những mặt phẳng nào dưới đây chứa đường thẳng SC?
(SAC).
(SAD).
(SBC).
(ABCD).
(SAB).
(SDC).
Câu 3 (1đ):
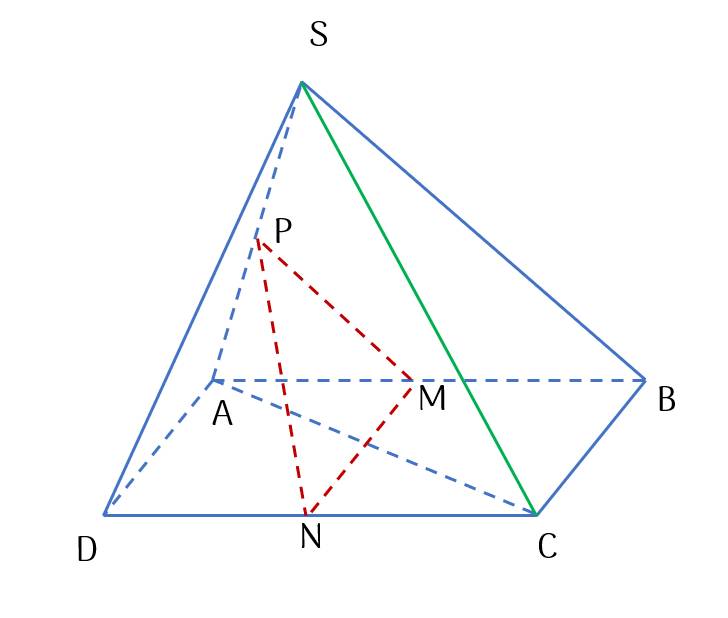
P là điểm chung của (MNP) và
(SAC).
(SBC).
(SDC).
Câu 4 (1đ):
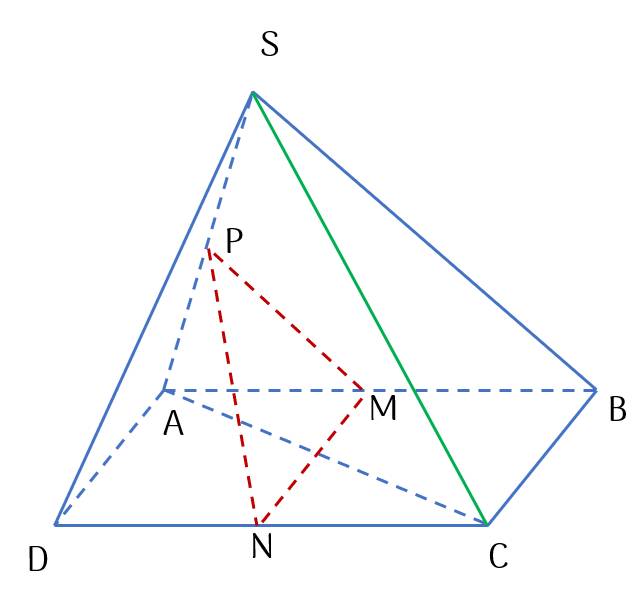
Đường thẳng nào của (SAC) đồng phẳng với đường thẳng MN?
SA.
SC.
AC.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin chào cây học sinh trong bài giảng
- lần này thầy sẽ mang đến cho khen dạng
- bài tập ở bài 3 đường thẳng và mặt phẳng
- song song
- trước hết thì một nhất lại vì bài toán
- tìm giao điểm giữa đường thẳng d và mặt
- phẳng P
- thì bài toán này chúng ta sẽ dựng đường
- thẳng d phẩy nằm trong mặt phẳng P nhưng
- lại đồng phẳng với đường thẳng d
- và đến nay chúng ta chỉ cần tìm giao
- điểm giữa D và bên phải thì chúng ta sẽ
- có ngay giao điểm giữa đường thẳng d và
- mặt phẳng P
- tự nhiên đến lưng thẳng d song song với
- đường thẳng d phẩy thì sao
- Ừ
- thì chúng ta có dạng toán hôm nay chứng
- minh đường thẳng d song song với mặt
- phẳng P A
- em về các bước làm chứng minh đường
- thẳng d song song với mặt phẳng P
- thì cũng cần như tương tự đối với Tìm
- giao điểm giữa đường thẳng d và mặt
- phẳng P
- cụ thể để như chúng ta tìm được đường
- thẳng d phải nằm trong mặt phẳng P mà
- lại song song với đường thẳng d thì bây
- giờ thay vì chúng ta cho đê cắt đây phải
- để tìm điểm chung giữa D và mặt phẳng P
- thì chúng ta sẽ kết luận đường thẳng d
- song song với mặt phẳng P
- thế như đường thẳng đấy vậy thuộc mặt
- phẳng P và đồng phẳng mới đây không dễ
- nhìn thấy thì chúng ta cần dựng một tài
- khoản quy
- chứa đường thẳng d và tiếp theo là tìm
- giao tuyến giữa P và quy ăn nhậu tại D
- phải và bây giờ để chứng minh đi song
- song với P thì chúng ta chỉ cần chứng
- minh đường thẳng d song song với cái
- giao tuyến Lê phần ta vừa Rực Rỡ
- ừ ừ
- hai mặt phẳng Q chúng ta vừa dụng
- chứa đường thẳng d và p phẩy là giao
- tuyến của P và Q Nếu d song song với d
- phải thì D sẽ song song với mặt phẳng P
- ừ ừ
- Ừ để hiểu rõ hơn các bước nào đối với
- bài toán chứng minh đường thẳng d song
- song với mặt phẳng P thì chúng ta cùng
- đi và bài tập
- a Cho hình chóp SABCD có đáy ABCD là
- hình bình hành à
- A có M là trung điểm AB
- cơ bản đồ là trung điểm CD
- MN trong đường thẳng
- d và yêu cầu chúng ta Chứng minh MN song
- song với SBC
- MN song song với SD
- anh ạ
- a đối với việc Chứng minh MN song song
- với SC thì ta thấy ngay đường thẳng MN
- song song với đường thẳng bc do MN là
- đường trung bình của hình thang ABCD để
- chúng ta có AD và BC là đáy của hình
- thang a
- anh vào da đỏ MN sẽ song song với BC
- Ông bà ta có ngay MN song song SBC tương
- tự chúng ta cũng có MN song song với a d
- và dao đó MN cũng song song với SD
- anh như vậy từ giả thiết chúng ta suy ra
- MN là đường trung bình của hình thang
- ABCD
- với AD và BC là hai đáy Tính từ đó suy
- ra MN song song với AB và MN không song
- song với BC
- ở thời tiếp theo chúng ta lại lập luận
- AD nằm trong SD BC nằm trong SBC là tam
- kết một MN song song với mặt phẳng SAD
- và MN song song với mặt phẳng SBC
- khi
- tiếp theo chúng ta sang câu b e
- cho cô bé yêu cầu chúng ta và F P là
- trung điểm AB a
- ở đây là trung điểm AB a
- anh
- chứng minh sc song song với MNP
- mặt phẳng MNP ê
- Ê tụi bay này chúng ta chưa thấy được
- đường thẳng nào của mặt phẳng MNP đồng
- phẳng với đường thẳng SC cả Vì thế nên
- chúng ta từng dựng một đường thẳng đồng
- phẳng với SC mà nằm trong mặt phẳng MNP
- đầu tiên ta có SC
- nằm xong
- SBC
- hoặc là SD
- C2 là mặt sp chúng tạo hay dùng
- đến nơi chúng ta lại đối mặt với 3 bài
- toán tìm giao tuyến giữa SBC và MNP SBC
- và MNP và cuối cùng là với mặt phẳng MNP
- à đến chỗ này thì thấy thấy bài này cũng
- tương tự với cách chúng ta chọn ra bài
- toán tìm giao tuyến dễ nhất đối với phần
- thiết diện
- cụ thể hơn ta thấy tam giác MNP được cấu
- tạo bởi ba đoạn thẳng a i m n và p n Tất
- nhiên là chúng ta sẽ không chọn đường
- thẳng t nào cho bức thứ hai Từng bước 2
- đường thẳng đồng phẳng
- chúng ta sẽ chọn là MN hoặc là MV do M N
- thuộc mặt phẳng ABCD của hình chóp và p
- m thuộc mặt phẳng SAB của hình chóp
- anh ở đây thời sự giữa đoạn đường thẳng
- MN và
- như vậy điểm chung thứ nhất của chúng ta
- cần điền P
- a
- b là điểm chung giữa 2 mặt phẳng MNP và
- sexy Ê
- xin lỗi A7 C
- Sapa là điểm Trung thứ nhất thì nên
- chúng ta chỉ xét từ thẳng MN trong MNP ở
- trong bước Thứ hai tạo ra hai đường
- thẳng đồng phẳng
- em
- có rõ ràng MN đồng phẳng với đường thẳng
- ac của mặt phẳng SAC C
- em gọi cho ABCD chúng ta cho MN cắt AC
- tại điểm O và ta có ngay giao tuyến xe
- đạp do đó
- vì
- vậy trong mặt phẳng ABCD có AC cắt MN
- tại O O
- suy ra giao tuyến chúng ta cần tìm giữa
- MNP với kaycee là tê lo
- qua góc với giao tuyến Boss này rồi thì
- chúng ta có được đường thẳng to nằm
- trong MNP mà lại đồng phẳng đường thẳng
- SC
- cụ thể hơn chúng cùng nằm trong mặt
- phẳng SBC
- và SCD đồng phẳng
- tiếp theo chúng ta thường Chứng minh sc
- sẽ song song với thì giao tuyến tâyo này
- à
- khi chúng ta để ý Ta có P là trung điểm
- AB xa như vậy để chứng minh to song song
- với SC thì chúng ta sẽ cần chỉ ra O là
- trung điểm AC I Anh
- bảo là trung điểm AC chúng ta sẽ nhìn
- vào mặt phẳng đáy
- mặt phẳng đáy chúng ta có M là trung
- điểm AB B
- và MN song song với BC
- lên từ đây cũng suy ra được cho là trung
- điểm AC theo định lý đường trung bình
- trong tam giác abc abc
- ta có hai điều đó làm em lo song song
- với BC cho MN là đường trung bình
- tiếp theo là M là trung điểm của AB
- ý kiến thứ hai được là taxi ra cũng là
- trung điểm AC a
- I il là trung điểm AC rồi thì ra tiếng
- Anh chỉ ra đường trung bình của tam giác
- AC B
- Từ từ đang taxi Apo song song với SC
- lại nằm trong mặt phẳng MNP
- như vận SC song song với MNP
- thì và kem đi xong dạng đầu tiên của bài
- thứ ba
- cháu có tên là chú có lên
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây