Lý thuyết SVIP

I. PHƯƠNG TRÌNH MŨ

1. Phương trình mũ cơ bản

+ Cho $a^x=m$ với $0<a\ne1$

• Nếu $m\leq0$ thì phương trình vô nghiệm
• Nếu $m>0$ thì $a^x=m \Leftrightarrow x=\log_am$.

+ Ví dụ 1

2. Phương pháp đưa về cùng cơ số

+ Sử dụng các quy tắc biến đổi lũy thừa để đưa về các lũy thừa cùng cơ số và áp dụng kết quả:

Với $0<a\ne1$ ta có $a^{f(x)}=a^{g(x)} \Leftrightarrow f(x)=g(x)$

+ Ví dụ 2

3. Phương pháp lôgarit hóa

+ Sử dụng cho phương trình không cùng cơ số dạng $a^{f(x)}=b^{g(x)}$ (cơ số dương, khác $1$ và nguyên tố cùng nhau)

Lấy lôgarit cơ số $a$ hoặc $b$ cho hai về ta có $a^{f(x)}=b^{g(x)}  \Leftrightarrow \log_aa^{f(x)}=\log_ab^{g(x)}  \Leftrightarrow f(x)=g(x).\log_ab$.

+ Ví dụ 3

4. Phương pháp đặt ẩn phụ

+ Sử dụng khi phương trình có xuất hiện lũy thừa chung, ta đặt ẩn phụ $t$ cho lũy thừa chung đó để đơn giản phương trình

Khi đặt $t=a^x$, điều kiện $t>0$ thì $a^{2x}=(a^x)^2=t^2$; $a^{-x}=\dfrac 1t$,...

+ Phương trình $m.a^{2f(x)}+n.a^{f(x)+g(x)}+p.a^{2g(x)}=0$ ta chia cả hai vế cho $a^{2g(x)}$ và đặt ẩn $t=a^{f(x)-g(x)}$.

+ Phương trình $m.a^{2f(x)}+n.(ab)^{f(x)}+p.b^{2f(x)}=0$ ta chia cả hai vế cho $a^{2f(x)}$ và đặt ẩn $t=\left(\dfrac ab\right)^{f(x)}$.

+ Ví dụ 4

5. Phương pháp sử dụng tính đơn điệu của hàm số

+ Ý tưởng 1: Nhẩm 1 nghiệm và chứng minh đó là nghiệm duy nhất

B1. Biến đổi 2 về của phương trình sao cho 1 vế đồng biến (hoặc hàm hằng), 1 vế nghịch biến (hoặc hàm hằng)

B2. Nhẩm và chứng minh $x_0$ là nghiệm

B3. Chứng minh $x\ne x_0$ không là nghiệm

+ Ý tưởng 2 đưa về dạng $f(u)=f(v)$ và $f$ là hàm tăng hoặc giảm

Khi đó $f(u)=f(v) \Leftrightarrow u=v$

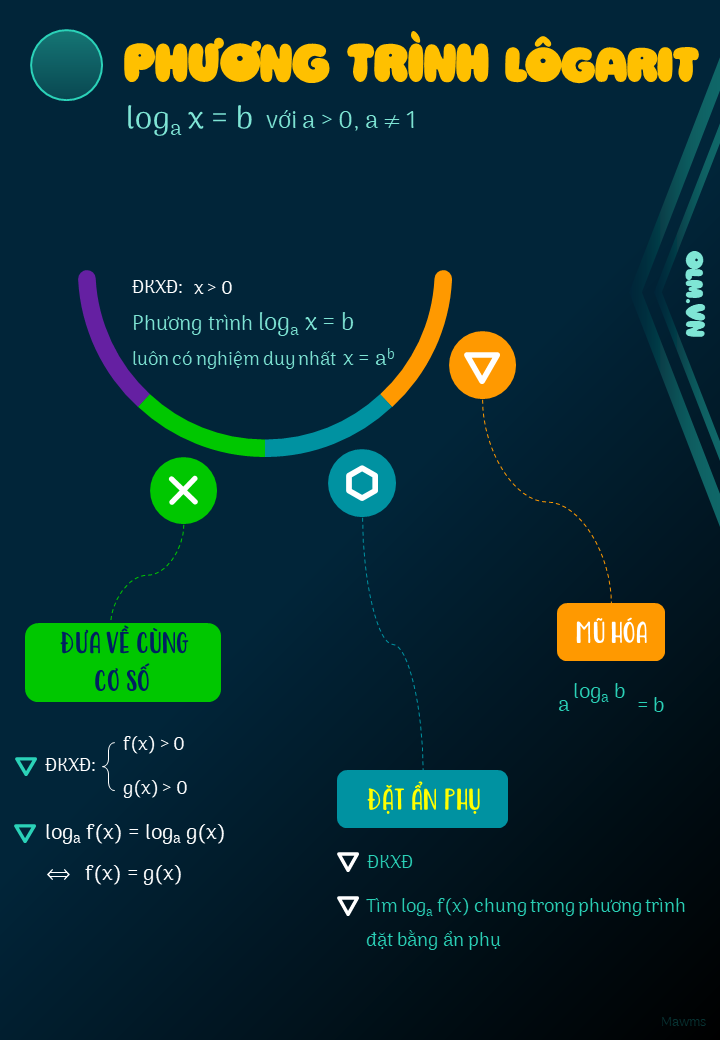
II. PHƯƠNG TRÌNH LÔGARIT

1. Phương trình lôgarit cơ bản

$\log_a x = m$ (với $0<a\ne 1$) $\Leftrightarrow x=a^m$.

Ví dụ 1.

2. Phương pháp đưa về cùng cơ số

+ Phương pháp chung: với $0<a \ne 1$ thì $\log_a x=\log_a y \Leftrightarrow$ \(\left\{{}\begin{matrix}x=y\\x>0\end{matrix}\right.\)

+ Ví dụ 2. 

3. Phương pháp đặt ẩn phụ

+ Phương pháp chung:

Đặt $\log_a f(x)$ chung trong phương trình là $t$. Đừa về phương trình ẩn $t$. Sau khi giải $t$ thay vào cách đặt để tìm $x$.

+ Chú ý:

Nếu $t=\log_a x$ thì

$\log_{\frac 1a}x = -t$;

$\log_{a^2} x=\dfrac t2$;

$\log_a^2 x=t^2$...

+ Ví dụ 3.

4. Phương pháp đánh giá hàm số

+Ý tưởng 1: biến đổi 2 vế của phương trình thành 2 hàm số không cùng chiều biến thiên

Phương pháp:

- Nhẩm và chứng minh $x_0$ là nghiệm

- Chứng minh $x_0$ là nghiệm duy nhất bằng cách chứng mình $x \ne x_0$ không phải là nghiệm

+ Ý tưởng 2: biến đổi phương trình về dạng $f(u)=f(v)$

Phương pháp: nếu $f(t)$ là hàm số tăng/ giảm thì $f(u)=f(v) \Leftrightarrow u=v$.