Lý thuyết SVIP

1. Khái niệm

Khái niệm

Hàm số \(y=x^{\alpha}\), với \(\alpha\inℝ\) được gọi là hàm số lũy thừa.

Chú ý

Tập xác định của hàm số lũy thừa \(y=x^n\), tùy thuộc vào giá trị của $n$. Cụ thể:

• Với $n$ nguyên dương, tập xác định là \(ℝ\).
• Với $n$ nguyên âm hoặc bằng 0, tập xác định là \(ℝ\backslash\left\{0\right\}\).
• Với $n$ không nguyên, tập xác định là \(\left(0;+\infty\right)\).

2. Đạo hàm của hàm số lũy thừa

Công thức tính đạo hàm của hàm hợp đối với hàm số lũy thừa:

\(\left(u^{\alpha}\right)'=\alpha.u^{\alpha-1}.u'\)

Ví dụ 1. \(\left(\left(2x^2+x-1\right)^{\dfrac{2}{3}}\right)'=\dfrac{2}{3}\left(2x^2+x-1\right)^{-\dfrac{1}{3}}.\left(2x^2+x-1\right)'=\dfrac{2\left(4x+1\right)}{3\sqrt[3]{2x^2+x-1}}\).

3. Khảo sát hàm số lũy thừa \(y=x^{\alpha}\)

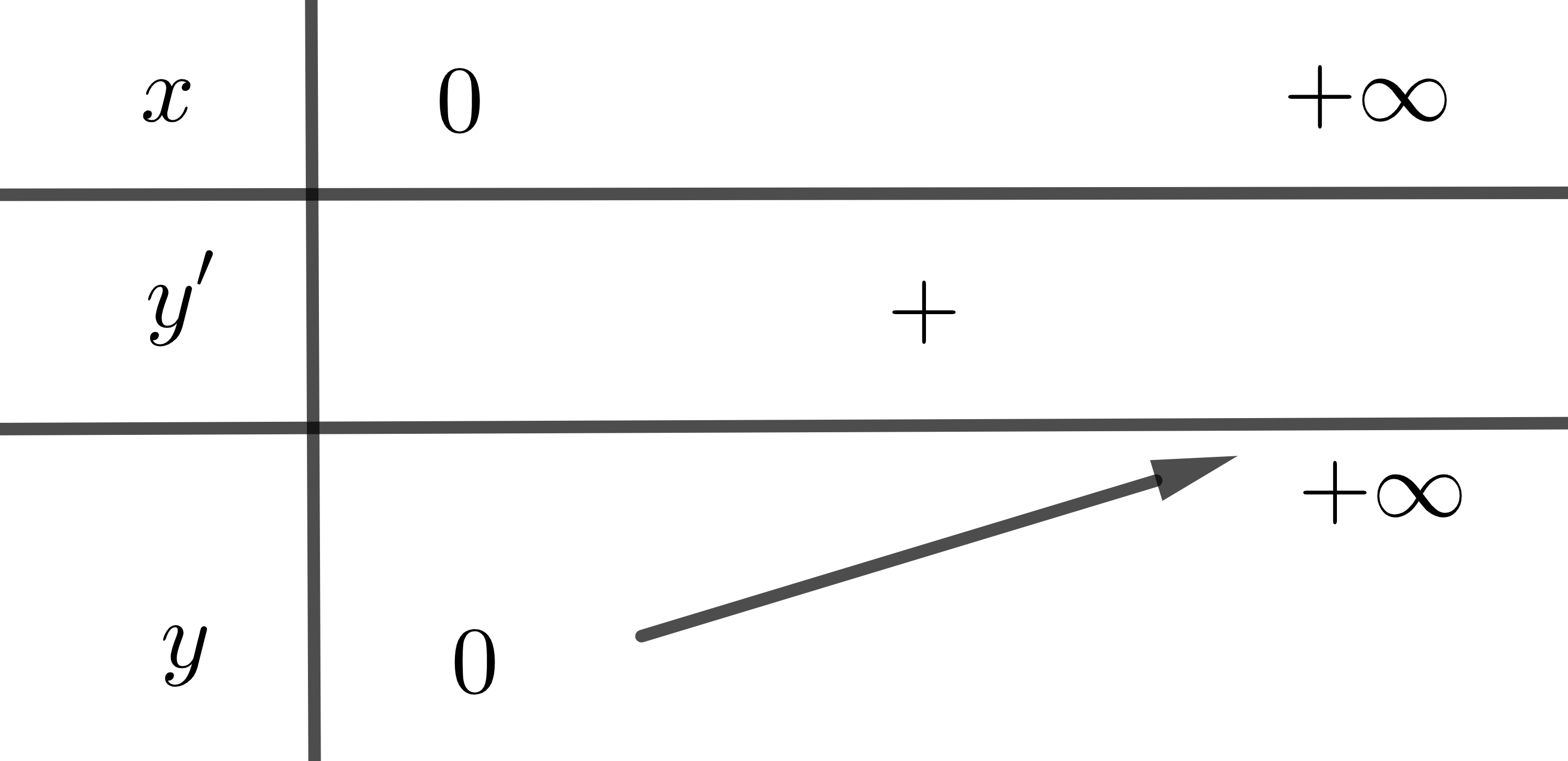
Khảo sát hàm số \(y=x^{\alpha}\) trên khoảng \(\left(0;+\infty\right)\)

	\(\alpha>0\)	\(\alpha< 0\)
Chiều biến thiên	Hàm số luôn đồng biến	Hàm số luôn nghịch biến
Bảng biến thiên
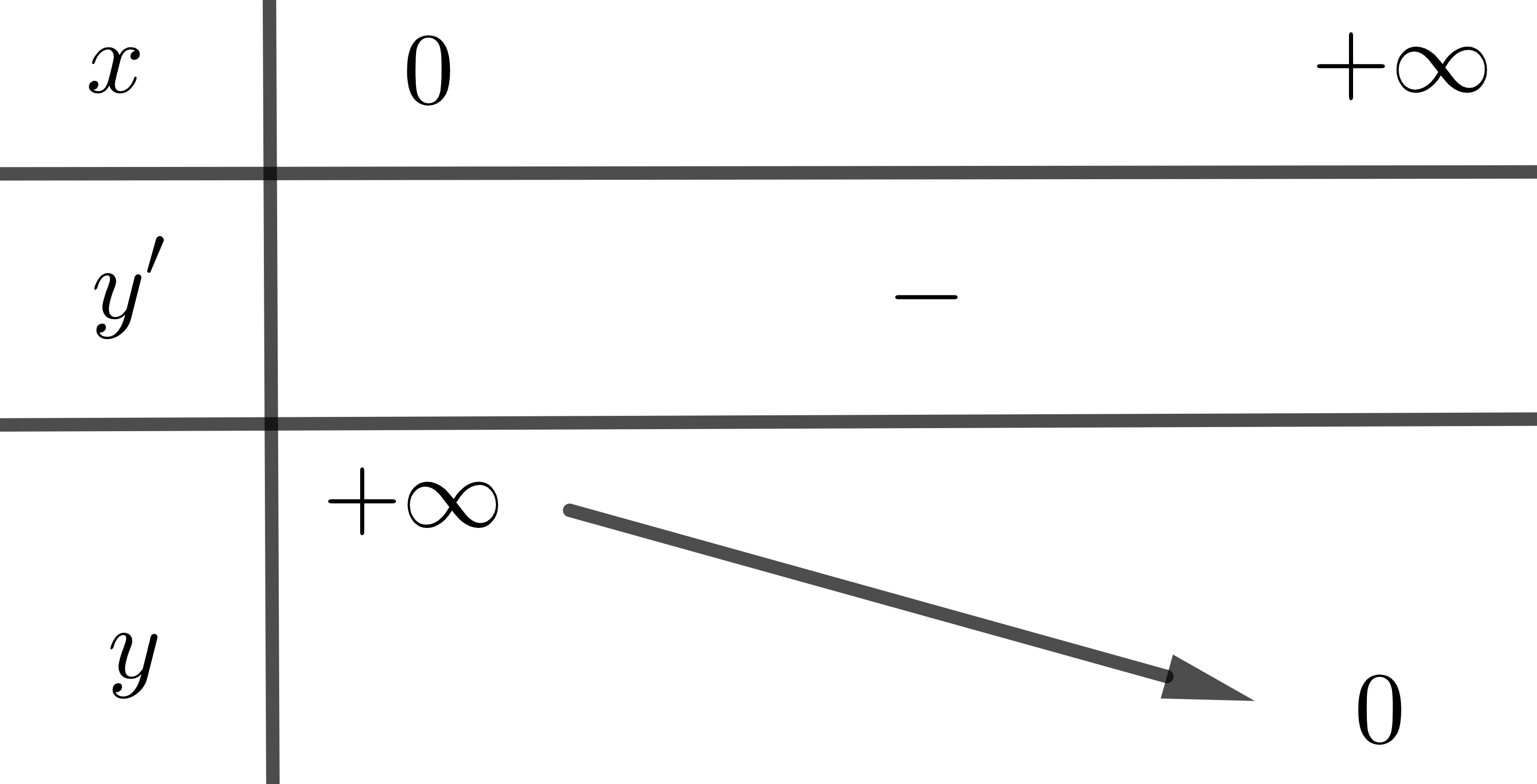Tiệm cận	Không có	Tiệm cận ngang là trục $Ox$ Tiệm cận đứng là trục $Oy$
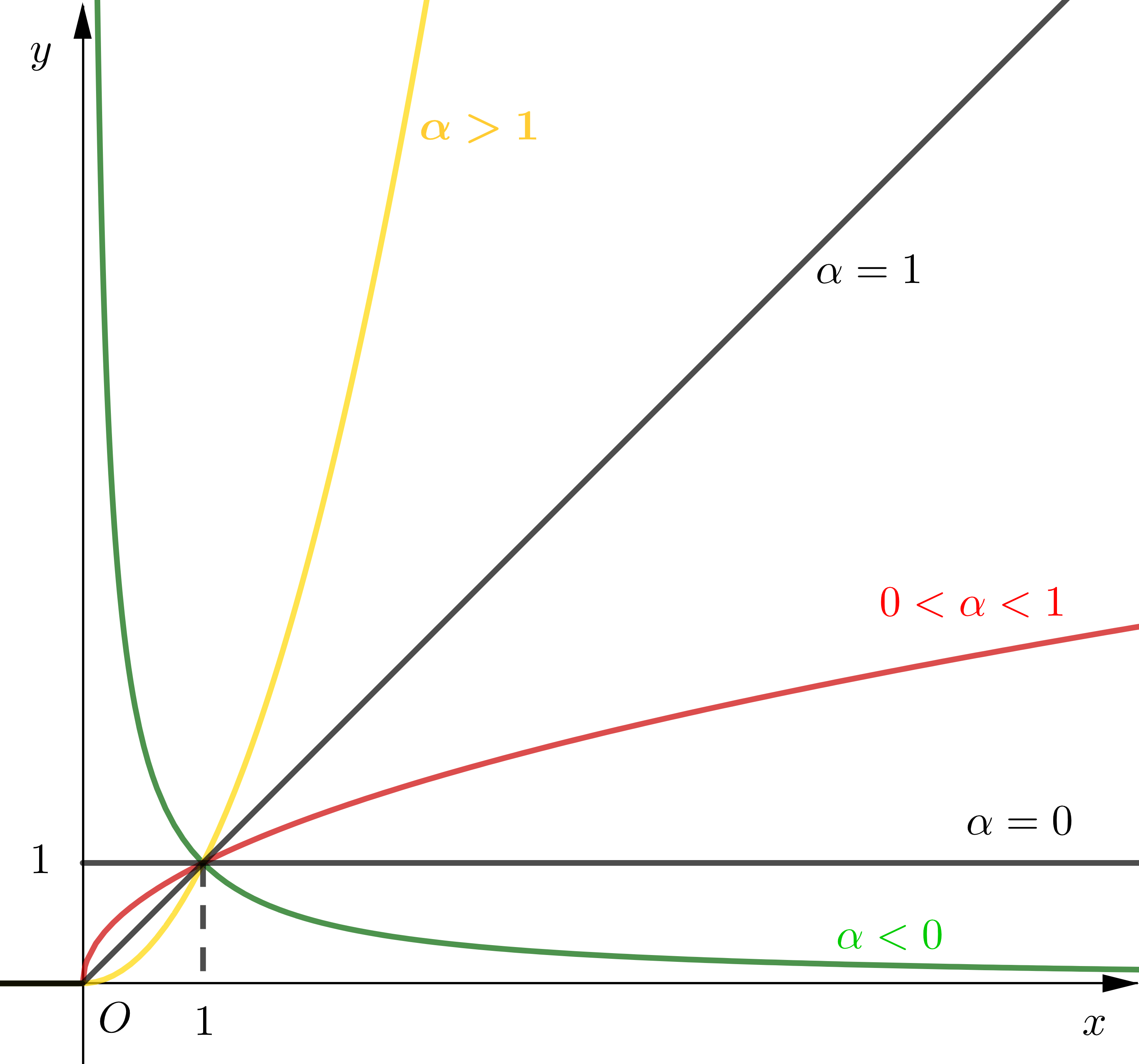
Đồ thị	Đồ thị luôn đi qua điểm $(1; 1)$

Chú ý

Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.

4. Bài toán lãi kép

Cho số vốn $P_0$, gửi theo hình thức lãi kép trong thời gian $n$ kì với lãi suất $r$ mỗi kì. 

Tổng số vốn và lãi nhận được sau $n$ kì là $P_n=P_0(1+r)^n$

Số lãi thu được sau $n$ kì là $P_n-P_0$.