Lý thuyết SVIP

I. Khái niệm cực đại, cực tiểu

Định nghĩa: Hàm số \(y=f\left(x\right)\) xác định và liên tục trên khoảng \(\left(a;b\right)\) (có thể a là \(-\infty\), b là \(+\infty\) ) và điểm \(x_0\in\left(a;b\right)\).

a) Nếu tồn tại số \(h>0\) sao cho \(f\left(x\right)< f\left(x_0\right)\) với mọi \(x\in\left(x_0-h;x_0+h\right)\) và \(x\ne x_0\) thì ta nói hàm số \(f\left(x\right)\) đạt cực đại tại \(x_0\).

b) Nếu tồn tại số \(h>0\) sao cho \(f\left(x\right)>f\left(x_0\right)\) với mọi \(x\in\left(x_0-h;x_0+h\right)\) và \(x\ne x_0\) thì ta nói hàm số \(f\left(x\right)\) đạt cực tiểu tại \(x_0\).

Chú ý:

1) Nếu hàm số \(f\left(x\right)\) đạt cực đại (cực tiểu) tại \(x_0\) thì \(x_0\) được gọi là điểm cực đại (điểm cực tiểu) của hàm số; \(f\left(x_0\right)\) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là \(f_{CĐ}\) (\(f_{CT}\)), còn điểm \(M\left(x_0;f\left(x_0\right)\right)\)  được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

2) Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

3) Nếu  hàm số \(y=f\left(x\right)\) có đạo hàm trên \(\left(a;b\right)\) và đạt cực đại hoặc cực tiểu tại \(x_0\) thì \(f'\left(x_0\right)=0\).

II. Điều kiện đủ để hàm số có cực trị

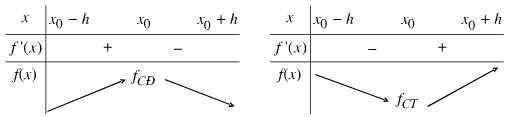
Định lý 1:  Giả sử hàm số \(y=f\left(x\right)\) liên tục trên khoảng \(K=\left(x_0-h;x_0+h\right)\) và có đạo hàm trên K hoặc trên \(K\backslash\left\{x_0\right\}\), với \(h>0\).a) Nếu \(f'\left(x\right)>0\) trên khoảng \(\left(x_0-h;x_0\right)\) và \(f'\left(x\right)< 0\) trên khoảng \(\left(x_0;x_0+h\right)\) thì \(x_0\) là một điểm cực đại của hàm số \(f\left(x\right)\).

b)  Nếu \(f'\left(x\right)< 0\) trên khoảng \(\left(x_0-h;x_0\right)\) và \(f'\left(x\right)>0\) trên khoảng \(\left(x_0;x_0+h\right)\) thì \(x_0\) là một điểm cực tiểu của hàm số \(f\left(x\right)\).

    

III. Qui tắc tìm cực trị

Qui tắc 1:

1. Tìm tập xác định.

2 Tính \(f'\left(x\right)\) . Tìm các điểm tại đó \(f'\left(x\right)\) bằng 0 hoặc không xác định.

3. Lập bảng biến thiên.

4. Từ bảng biến thiên suy ra các điểm cực trị.

Định lý 2: Giả sử hàm số \(y=f\left(x\right)\) có đạo hàm cấp hai trong khoảng \(\left(x_0-h;x_0+h\right)\), với \(h>0\). Khi đó:

a) Nếu \(f'\left(x_0\right)=0,f''\left(x_0\right)>0\) thì \(x_0\) là điểm cực tiểu;

b) Nếu \(f'\left(x_0\right)=0,f''\left(x_0\right)< 0\) thì \(x_0\) là điểm cực đại.

Áp dụng Định lý 2 ta có qui tắc sau đây để tìm cực trị của hàm số.

Qui tắc 2:

1. Tìm tập xác định.

2. Tính \(f'\left(x\right)\). Giải phương trình \(f'\left(x\right)=0\) và kí hiệu \(x_i\) (\(i=1,2,...,n\)) là tập các nghiệm của nó.

3. Tính \(f''\left(x\right)\) và \(f''\left(x_i\right)\).

4. Dựa vào dấu của \(f''\left(x_i\right)\) suy ra tính chất cực trị của điểm \(x_i\).