Bài học cùng chủ đề
- Khoảng biến thiên và khoảng tứ phân vị
- Phương sai và độ lệch chuẩn
- Một số ví dụ và công thức khác của phương sai và độ lệch chuẩn
- Phát hiện giá trị ngoại lệ (giá trị bất thường) bằng biểu đồ hộp
- Luyện tập
- Một số bài tập có hướng dẫn (Sách bài tập toán 10 KNTTVCS)
- Phiếu bài tập: Các số đặc trưng đo độ phân tán
- Các số đặc trưng đo độ phân tán
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Luyện tập SVIP
Chọn những khẳng định đúng.
Cho hai mẫu số liệu.
| A | B |
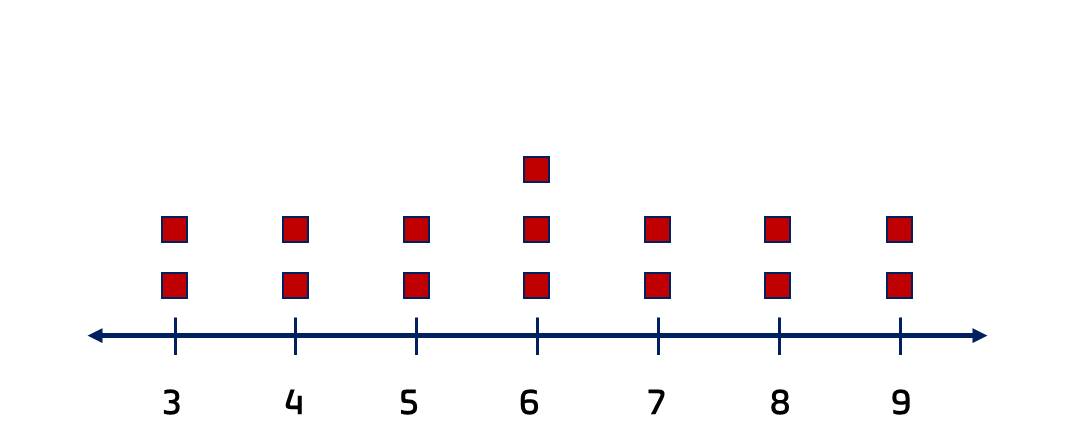 |
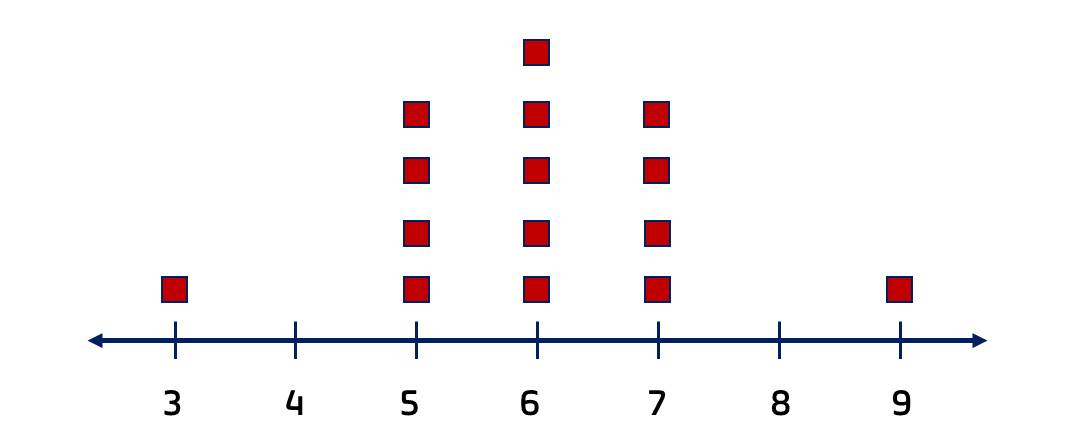 |
Không tính toán, chọn phương án đúng.
Hai mẫu số liệu này có cùng khoảng biến thiên không?
Cho hai mẫu số liệu.
| A | B |
 |
 |
Không tính toán, chọn phương án đúng?
Số trung bình của hai mẫu số liệu có bằng nhau không?
Cho hai mẫu số liệu.
| A | B |
 |
 |
Không tính toán, chọn phương án đúng?
Phương sai của mẫu số liệu nào lớn hơn?
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau.
Khi nhân đôi các giá trị ở trong mẫu số liệu, khoảng biến thiên mới
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau.
Khi nhân đôi các giá trị ở trong mẫu số liệu, số trung bình mới
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau.
Khi nhân đôi các giá trị ở trong mẫu số liệu, độ lệch chuẩn mới
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau.
Khi cộng các giá trị ở trong mẫu số liệu với 2 đơn vị, khoảng biến thiên mới
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau.
Khi cộng các giá trị ở trong mẫu số liệu với 2 đơn vị, số trung bình mới
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau.
Khi cộng các giá trị ở trong mẫu số liệu với 2 đơn vị, độ lệch chuẩn mới
Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được: Giá trị nhỏ nhất bằng 25; các tứ phân vị lần lượt là Q1 = 36 ; Q2 = 60 ; Q3 = 100; giá trị lớn nhất bằng 205.
Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là
Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được: giá trị nhỏ nhất bằng 25; các tứ phân vị lần lượt là Q1 = 36 ; Q2 = 60 ; Q3 = 100; giá trị lớn nhất bằng 205.
Những khoảng nào dưới đây chứa 50% giá trị của mẫu số liệu.
Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được: Giá trị nhỏ nhất bằng 25; các tứ phân vị lần lượt là Q1 = 36 ; Q2 = 60 ; Q3 = 100; giá trị lớn nhất bằng 205.
Khoảng tứ phân vị của mẫu số liệu trên bằng
Cho mẫu số liệu:
2,977 3,155 3,920 3,412 4,236
2,593 3,270 3,813 4,042 3,387
Khoảng biến thiên của mẫu số liệu này là
Cho mẫu số liệu:
2,977 3,155 3,920 3,412 4,236
2,593 3,270 3,813 4,042 3,387
Khoảng tứ phân vị của mẫu số liệu trên là
Cho mẫu số liệu:
2,977 3,155 3,920 3,412 4,236
2,593 3,270 3,813 4,042 3,387
Phương sai của mẫu số liệu trên là
(Tất cả các kết quả được làm tròn đến hàng phần chục nghìn hay chữ số thập thân thứ tư).
Tỉ lệ thất nghiệp ở một số quốc gia vào năm 2007 (đơn vị %) được cho như sau:
7,8 3,2 7,7 8,7 8,6 8,4 7,2 3,6
5,0 4,4 6,7 7,0 4,5 6,0 5,4
Mẫu số liệu trên có bao nhiêu giá trị bất thường?


Bạn có thể đánh giá bài học này ở đây