Dao động điều hòa SVIP

1. Dao động cơ

Chiếc thuyền nhấp nhô tại chỗ neo, dây đàn guitar rung động...là một số ví dụ về vật dao động. Chúng chuyển động qua lại xung quanh một vị trí đặc biệt gọi là vị trí cân bằng.

Những chuyển động như vậy được gọi là dao động cơ.

Dao động cơ của một vật được chia làm hai loại: tuần hoàn và không tuần hoàn.

• Dao động tuần hoàn là dao động mà sau những khoảng thời gian bằng nhau vật trở lại vị trí cũ theo hướng cũ. Ví dụ: con lắc đồng hồ dao động tuần hoàn.

• Dao động tuần hoàn đơn giản nhất là dao động điều hòa.

2. Dao động điều hòa

Dao động điều hòa là dao động trong đó li độ của vật là một hàm côsin (hay sin) của thời gian.

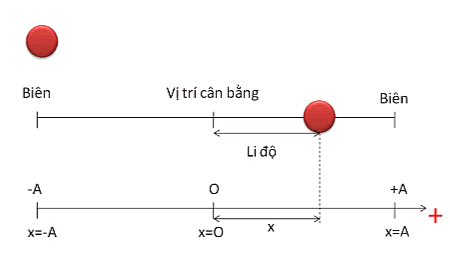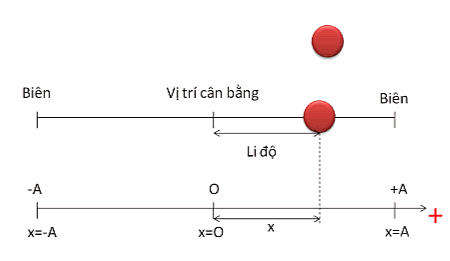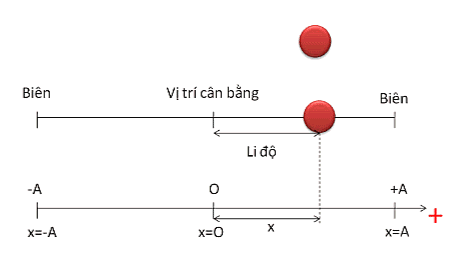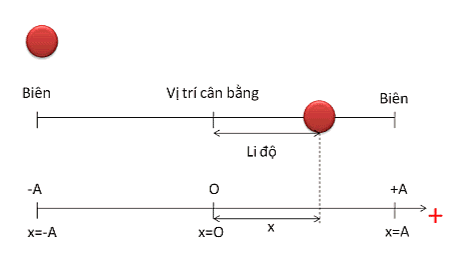
Phương trình dao động điều hòa \(x=A\cos\left(\omega t+\varphi\right)\)

Trong đó:

• x là khoảng cách từ vật đến vị trí cân bằng
• A là biên độ dao động của vật
• \(\omega\) là tần số góc (rad/s)
• \(\left(\omega t+\varphi\right)\) là pha của dao động 
•  \(\varphi\) là pha ban đầu

3. Chu kì. Tần số. Tần số góc của dao động điều hòa

• Chu kì (T) của dao động điều hòa là khoảng thời gian vật thực hiện một dao động toàn phần.
• Giữa tần số góc, chu kì và tần số có mối liên hệ

\(\omega=\frac{2\pi}{T}=2\pi f.\)

4. Vận tốc và gia tốc của vật dao động điều hòa

• Vận tốc là đạo hàm của li độ theo thời gian

\(v=x'=-\omega A\sin\left(\omega t+\varphi\right)\)

     Vận tốc bằng 0 khi \(x=\pm A\) (vị trí biên).

     Vận tốc cực đại \(v_{max}=\omega A\) khi \(x=0\) (vị trí cân bằng).

• Gia tốc là đạo hàm của vận tốc theo thời gian

\(a=v'=-\omega^2A\cos\left(\omega t+\varphi\right)\)

hay \(a=-\omega^2x\)

     Gia tốc bằng 0 khi \(x=0\) (vị trí cân bằng).

     Gia tốc luôn ngược dấu với li độ và có độ lớn tỉ lệ với độ lớn của li độ.

5. Đồ thị của dao động điều hòa

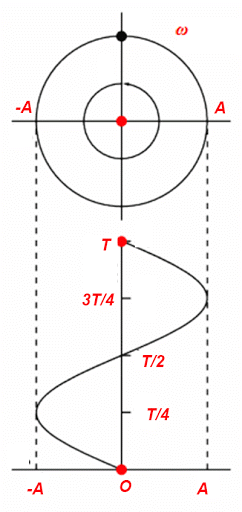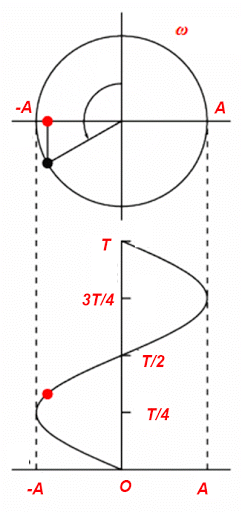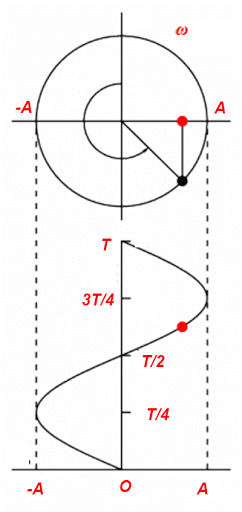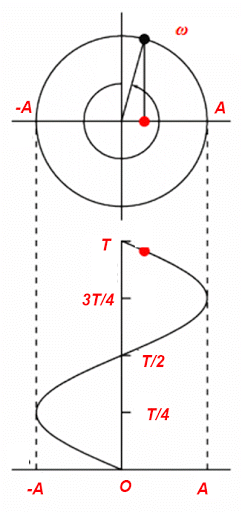
Đồ thị của dao động điều hòa là một đường hình sin.