Khái niệm vectơ SVIP

1. ĐỊNH NGHĨA VECTƠ

Vectơ là một đoạn thẳng có hướng, nghĩa là ta đã chỉ ra điểm đầu và điểm cuối.

• Vectơ có điểm đầu là \(A\) và điểm cuối \(B\) được kí hiệu là \(\overrightarrow{AB}\) đọc là vectơ \(AB\).

• Đường thẳng đi qua hai điểm \(A\) và \(B\) là giá của vectơ \(\overrightarrow{AB}\).
• Độ dài đoạn thẳng \(AB\) là độ dài của vectơ \(\overrightarrow{AB}\), kí hiệu là \(\left|\overrightarrow{AB}\right|\).

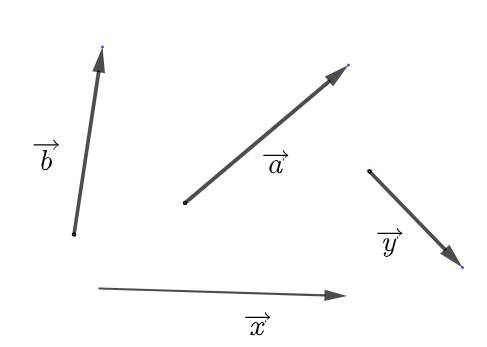
Chú ý: Vectơ còn được kí hiệu là \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y},...\) 

 2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Nhận xét: Nếu hai vectơ cùng phương thì hoặc chúng cùng hướng hoặc chúng ngược hướng.

Ví dụ: Trong hình vẽ sau

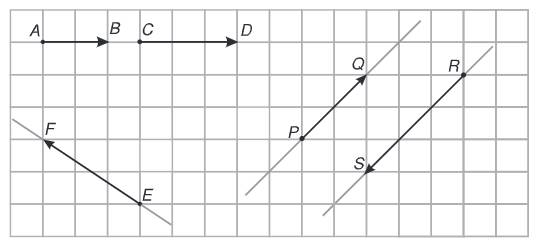
Ta có:

• Vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\) có giá trùng nhau. Vectơ \(\overrightarrow{PQ}\) và \(\overrightarrow{RS}\) có giá song song với nhau.
• Có hai cặp vectơ cùng phương với nhau là:  \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\) ; \(\overrightarrow{PQ}\) và \(\overrightarrow{RS}\).
• Vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\) là hai vectơ cùng hướng. Vectơ \(\overrightarrow{PQ}\) và \(\overrightarrow{RS}\) là hai vectơ ngược hướng.

Nhận xét: Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng phương.

3. VECTƠ BẰNG NHAU - VECTƠ ĐỐI NHAU

• Hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) được gọi là bằng nhau nếu chúng có  cùng hướng và cùng độ dài , kí hiệu là \(\overrightarrow{a}=\overrightarrow{b}\).
• Hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) được gọi là đối nhau nếu chúng ngược  hướng và cùng độ dài , kí hiệu là \(\overrightarrow{a}=\overrightarrow{-b}\). Khi đó vectơ \(\overrightarrow{b}\) được gọi là vectơ đối của vectơ \(\overrightarrow{a}.\)

Chú ý: 

• Cho vectơ \(\overrightarrow{a}\) và điểm \(O\), ta luôn tìm được một điểm \(A\) duy nhất sao cho \(\overrightarrow{OA}=\overrightarrow{a}.\) Độ dài của vectơ \(\overrightarrow{a}\) là độ dài đoạn \(OA\), kí hiệu là \(\left|\overrightarrow{a}\right|\).
• Cho đoạn thẳng \(MN\), ta luôn có \(\overrightarrow{NM}=-\overrightarrow{MN}.\)

4. VECTƠ-KHÔNG

Vectơ có điểm đầu và điểm cuối trùng nhau gọi là vectơ-không, kí hiệu là \(\overrightarrow{0}.\)

 Chú ý:

- Quy ước vectơ-không có độ dài bằng \(0.\)

- Vectơ-không luôn cùng phương, cùng hướng với mọi vectơ.

- Mọi vectơ-không đều bằng nhau:\(\overrightarrow{0}=\overrightarrow{AA}=\overrightarrow{BB}=\overrightarrow{CC}=...\) với mọi điểm \(A,B,C,...\)

- Vectơ đối của vectơ-không là chính nó.