Hệ thức lượng trong tam giác vuông SVIP

Hướng dẫn giải:

\(\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}=\dfrac{BH}{CH}=\dfrac{x}{y}\Rightarrow\dfrac{x}{y}=\dfrac{25}{36}.\)

Đặt $x=25t,$ $y=36t$.

Ta có $AH^2 = 30^2 = xy = 900t^2\Rightarrow t = 1$.

Suy ra $x = 25,$ $y=36$.

Hướng dẫn giải:

a) $HB.HC = AF.AC = AH^2$.

b) $S_{AEHF} = AE.AF$.

Theo câu a thì $AE.AF.AB.AC = AH^4$, mà $AB.AC = AH.BC$ nên $AE.AF=\dfrac{AH^3}{BC}$.

Gọi $M$ là trung điểm $BC$ thì $AM=\dfrac12 BC$ (cố định), $AH\le AM$ nên $S_{AEHF}$ lớn nhất khi và chỉ khi $H$ trùng $M$.

Hướng dẫn giải:

a) Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
\(AH^2=BH.HC\)\(\Leftrightarrow HC=\dfrac{AH^2}{HB}=2,25cm\).
\(BC=BH+HC=4+2,25=6,25cm\).
\(AM=\dfrac{BC}{2}=3,125cm\).
b) Áp dụng định lý Pi-ta-go ta có:
\(AB=\sqrt{AH^2+BH^2}=5cm\).
 \(AC=\sqrt{BC^2-AB^2}=\sqrt{6,25^2-5^2}=3,75cm\).
Theo tính chất tia phân giác của một góc:\(\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{5}{3,75}=\dfrac{4}{3}\).

Gọi E, F là chân đường vuông góc hạ từ D xuống AC và AB. Ta thấy ngay FDEA là hình vuông nội tiếp tam giác vuông ABC.

Từ đó ta có \(\dfrac{DE}{AB}=\dfrac{DC}{BC}=\dfrac{3}{7}\Rightarrow DE=\dfrac{3}{7}.5=\dfrac{15}{7}\left(cm\right)\)

\(\Rightarrow AD=\dfrac{15\sqrt{2}}{7}\left(cm\right)\).

Hướng dẫn giải:

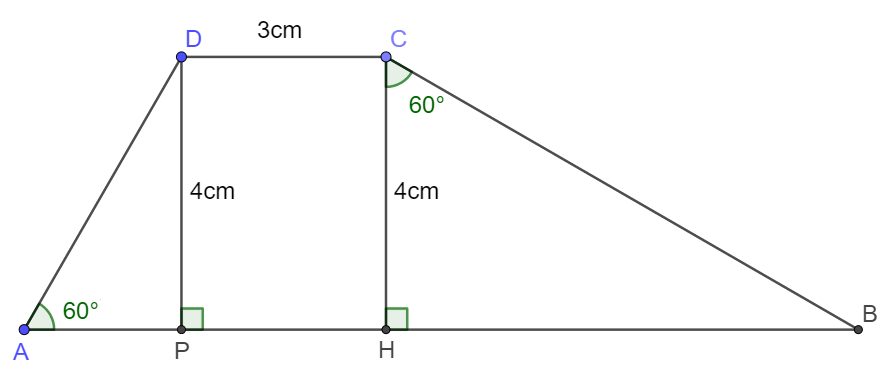
Áp dụng tỉ số lượng giác của góc nhọn, ta có:
\(AP=DP.cot\widehat{DAP}=\dfrac{4\sqrt{3}}{3}\left(cm\right)\).
\(HB=CH.tan\widehat{HCB}=4\sqrt{3}\left(cm\right)\).
\(DA.sin\widehat{DAP}=DP\Leftrightarrow DA=\dfrac{DP}{sin\widehat{DAP}}=\dfrac{8\sqrt{3}}{3}\).
Tương tự:

 \(CB=\dfrac{CH}{cos\widehat{HCB}}=\dfrac{4}{cos60^o}=8\left(cm\right)\).
\(AB=AP+PH+HB=\dfrac{4\sqrt{3}}{3}+3+4\sqrt{3}\) \(=\dfrac{16\sqrt{3}}{3}+3\left(cm\right)\).
Diện tích hình thang ABCD là:
\(\dfrac{\left(DC+AB\right).CH}{2}=\dfrac{\left(3+3+\dfrac{16\sqrt{3}}{3}\right).4}{2}=2\left(6+\dfrac{16\sqrt{3}}{3}\right)\left(cm^2\right)\)

Chu vi hình thang ABCD là: \(\dfrac{16\sqrt{3}}{3}+3+3+\dfrac{8\sqrt{3}}{3}+8=14+8\sqrt{3}\left(cm\right)\)

Hướng dẫn giải:

Đặt $CD = x,$ $AC = y$.

Ta có: $10.x = 6.y$ ($=S_{ABC}$)

Suy ra $\dfrac xy = \dfrac35$.

Đặt $x = 3t,$ $y=5t$.

Áp dụng định lí Pi-ta-go vào tam giác vuông $ACD$ tìm được $t=2$.

Vậy $x=6,$ $S_{ABC}=60cm^2$.

Hướng dẫn giải:

a) Chia cả tử và mẫu cho $\cos \alpha$ được \(\dfrac{2+3\tan\alpha}{3-4\tan\alpha}\).

Đáp số: $-\dfrac{11}{9}$.

b) Chia cả tử và mẫu cho $\cos \alpha$ được \(\dfrac{\tan\alpha}{\tan^2\alpha-\tan\alpha+1}\).

Đáp số: $\dfrac{3}{7}$.

Hướng dẫn giải:

Áp dụng: $\sin ^2 \alpha + \cos^2 \alpha = 1$ và $\tan \alpha =\dfrac{\sin \alpha}{\cos \alpha}$.

a) $\cos ^2 \alpha$.

b) $1$.

c) $\sin ^2 \alpha$.

d) chú ý: biểu thức trong ngoặc bằng $\cos^2 \alpha$.

Đáp số: $\sin ^2 \alpha$.

Hướng dẫn giải:

a) Tứ giác AEHD là hình chữ nhật (tứ giác có 3 góc vuông).
Vì vậy DE = AH.
Áp dụng hệ thức lượng trong tam giác vuông, ta có: 
\(AH^2=BH.HC=4.9=36\Rightarrow AH=6\left(cm\right)\).
Vậy DE = AH = 6(cm).
b) Gọi O là giao điểm của AH và DE. Tứ giác ADHE là hình chữ nhật, suy ra OD = OH.
Xét tam giác DMO và tam giác HMO có:
MO chung
OD = OH
\(\widehat{ODM}=\widehat{OHM}=90^o\)
Suy ra \(\Delta DMO=\Delta HMO\) (ch - cgv).
Vì vậy \(DM=MH\). (1) 
Từ đó suy ra tam giác MDH cân tại M hay \(\widehat{MDH}=\widehat{DHM}\).
Có \(\widehat{BDM}+\widehat{MDH}=90^o,\widehat{DBH}+\widehat{DHB}=90^o\).
Suy ra \(\widehat{MDB}=\widehat{DBM}\). Vì vậy tam giác BDM cân tại M hay MB = MD.  (2)
Từ (1) và (2) suy ra BM = MH hay M là trung điểm của BH.
Chứng minh tương tự ta có N là trung điểm của CH.
c) Tứ giác EDMN là hình thang với đường cao DE, các đáy DM và EN.
DM = BH : 2 = 2(cm), EN = AH : 2 = 4,5(cm).
Diện tích hình thang EDMN là:
\(\dfrac{DE.\left(DM+EN\right)}{2}=\dfrac{6\left(2+4,5\right)}{2}=19,5\left(cm^2\right)\).

Hướng dẫn giải:

a) Tam giác ABC cân tại A có AH là đường cao nên H là trung điểm của BC.
Vì vậy BH = HC = 16 : 2 = 8(cm).
\(cos\widehat{ACB}=\dfrac{HC}{AC}=\dfrac{8}{10}=\dfrac{4}{5}\) suy ra \(\widehat{BCA}\cong36^o52'\).
Tam giác ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}=36^o52'\).
 \(\widehat{BAC}=180^o-\left(36^o52'+36^o52'\right)=106^o16'\).
b) Do CD//AH nên áp dụng định lý Ta-let ta có:

\(\dfrac{BH}{BC}=\dfrac{HI}{DC}=\dfrac{1}{2}\)
 Áp dụng định lý Pi-ta-go ta có:
 \(AH=\sqrt{AC^2-HC^2}=6\left(cm\right)\).
 Suy ra \(HI=\dfrac{2}{3}AH=4\left(cm\right)\).
 Vì vậy \(DC=2HI=2.4=8\left(cm\right)\).
 Diện tích tứ giác ABCD là:
 \(S_{\Delta ABC}+S_{\Delta ADC}=\dfrac{1}{2}AH.BC+\dfrac{1}{2}HC.DC\) \(=\dfrac{1}{2}.6.16+\dfrac{1}{2}.8.8=80\left(cm^2\right)\).

Hướng dẫn giải:

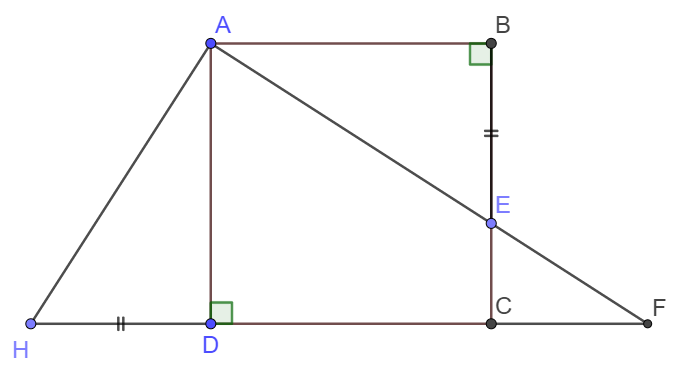
Dựng điểm H thuộc tia CD sao cho \(DH=BE.\).
Ta có \(\Delta ABE=\Delta ADH\left(c-g-c\right)\Rightarrow AE=AH\).
Áp dụng hệ thức lượng cho tam giác AHF: \(\widehat{HAF}=90^o;AD\perp HF\).
Ta có \(\dfrac{1}{AH^2}+\dfrac{1}{AF^2}=\dfrac{1}{AD^2}\) nên \(\dfrac{1}{AE^2}+\dfrac{1}{AF^2}=\dfrac{1}{AD^2}\).

Hướng dẫn giải:

Đặt $CH=x$ thì $BH = 21-x$.

Ta có: $AB^2 - BH^2 = AC^2 -CH^2$ ($=AH^2$)

Suy ra $10^2 - (21-x)^2 = 17^2 - x^2$.

Phương trình có nghiệm $x=6$.

Từ đó $AH=8$.

Diện tích tam giác bằng $84$ (đvdt).

Hướng dẫn giải:

a) Vì $\widehat{AEM}=\widehat{AFM}={90}^\circ$ nên A, E, M, F thuộc đường tròn tâm I đường kính AM $\Rightarrow\ \widehat{EIF}=2\widehat{EAF}={120}^\circ$ (góc ở tâm bằng hai lần góc nội tiếp chắn cung \(\stackrel\frown{EF}\)).

b) Hạ $IH\bot EF$, ta có $IE=IF=\frac{1}{2}AM$ nên $\Delta IEF$ cân $\Rightarrow HE=HF$.

Ta lại có: $EH=EI.\sin{\widehat{EIH}}=\frac{1}{2}AM.\sin{{60}^\circ}$ (vì $\widehat{EIH}=\widehat{FIH}=\frac{1}{2}\widehat{EIF}={60}^\circ$).

Suy ra $EH=\frac{a}{2}.\frac{\sqrt3}{2}=\frac{a\sqrt3}{4}\Rightarrow EF=2EH=\frac{a\sqrt3}{2}$.

c) EF nhỏ nhất khi AM nhỏ nhất $\Leftrightarrow$ AM $\bot$ BC.

Hướng dẫn giải:

a) Có $\widehat{BAD}={90}^\circ-\widehat{A_1};\ \widehat{BDA}={90}^\circ-\widehat{A_2}$.

Mà $\widehat{A_1}=\widehat{A_2}\Rightarrow\widehat{BAD}=\widehat{BDA}$. Do đó $\Delta BAD$ cân tại B.

b) Đặt $AB=x$ $(6 <x<25)$ thì $BD=x$, $BH = x-6$.

$BH.BC=AB^2\Rightarrow\left(x-6\right).25=x^2\Leftrightarrow x^2-25x+150=0 \Leftrightarrow x=10$ hoặc $x=15$.

Vậy $AB = 10cm$ hoặc $AB = 15cm$. 

Hướng dẫn giải:

Hạ $AH\bot BC$. Đặt $BH=x$ $\left(0<x<10\right)$ $\Rightarrow AH=x,$ $HC=10-x$.

$AH=HC.\tan{{30}^\circ}\Leftrightarrow x=\left(10-x\right)\frac{1}{\sqrt3} \Leftrightarrow\left(\sqrt3+1\right)x=10$

$\Leftrightarrow\left(\sqrt3+1\right)x=10\Leftrightarrow x=\frac{10}{\sqrt3+1}=5\left(\sqrt3-1\right).$

Suy ra $AH = 5(\sqrt{3}-1)$.

$AC=\frac{AH}{\sin{C}}=\frac{AH}{\sin{{30}^o}}=2.AH=10\left(\sqrt3-1\right)\ cm.$