Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Hàm số bậc hai. Đồ thị và ứng dụng SVIP
Nội dung này do giáo viên tự biên soạn.
I. HÀM SỐ BẬC HAI
Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng \(y=ax^2+bx+c,\) trong đó \(a,b,c\) là các hằng số và \(a\ne0.\)
Tập xác định của hàm số bậc hai là \(ℝ\).
Ví dụ: trong các hàm số sau, hàm số nào là hàm số bậc hai?
a)\(y=3x^3-2x+1\);
b)\(y=-2x^2+x+3\);
c)\(y=\dfrac{1}{x^2}-\dfrac{2}{x}+1\).
Giải
Hàm số \(y=-2x^2+x+3\) là hàm số bậc hai có hệ số của \(x^2\) là \(-2\), hệ số của \(x\) là \(1\), hệ số tự do là \(3.\)
Hàm số \(y=3x^3-2x+1\) và \(y=\dfrac{1}{x^2}-\dfrac{2}{x}+1\) không phải là hàm số bậc hai.
II. ĐỒ THỊ HÀM SỐ BẬC HAI
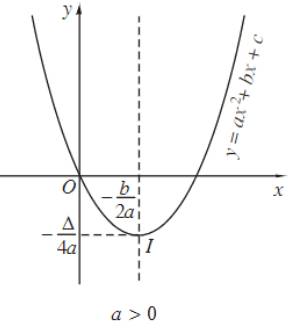
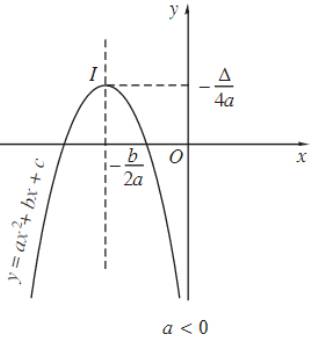
Đồ thị hàm số bậc hai \(y=ax^2+bx+c\left(a\ne0\right)\) là một đường parabol có đỉnh là điểm với tọa độ \(\left(-\dfrac{b}{2a};-\dfrac{\Delta}{4a}\right)\) và trục đối xứng là đường thẳng \(x=-\dfrac{b}{2a}.\)
|
|
|
Nhận xét: Cho hàm số \(f\left(x\right)=ax^2+bx+c\left(a\ne0\right)\) ta có \(-\dfrac{\Delta}{4a}=f\left(-\dfrac{b}{2a}\right).\)
Để vẽ đường parabol \(y=ax^2+bx+c\left(a\ne0\right)\) ta tiến hành theo các bước sau:
1. Xác định tọa độ đỉnh \(I\left(-\dfrac{b}{2a};-\dfrac{\Delta}{4a}\right);\)
2. Vẽ trục đối xứng \(x=-\dfrac{b}{2a}\);
3. Xác định một số điểm đặc biệt như: giao điểm của parabol với trục tung (có tọa độ \(\left(0;c\right)\)), trục hoành (nếu có), điểm đối xứng với điểm \(\left(0;c\right)\) qua trục đối xứng \(x=-\dfrac{b}{2a}\)
4. Vẽ parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số.
Chú ý: Nếu \(a>0\) thì parabol có bề lõm quay lên trên, nếu \(a< 0\) thì parabol có bề lõm quay xuống dưới.
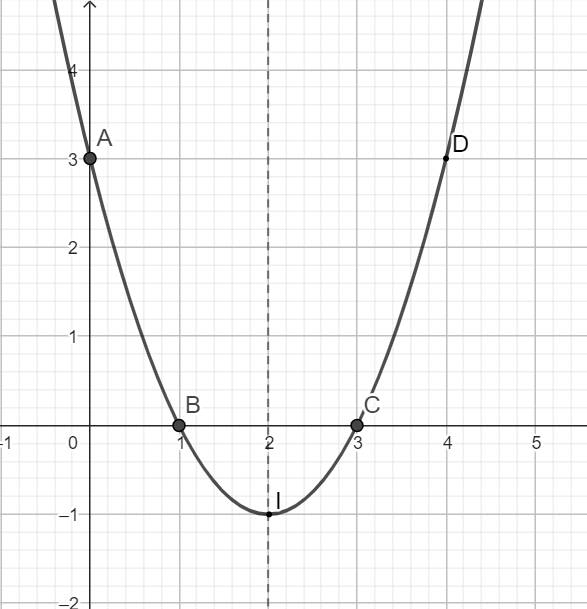
Ví dụ. Vẽ đồ thị hàm số \(y=x^2-4x+3\).
Giải
Tọa độ đỉnh \(I\left(2;-1\right)\);
Trục đối xứng \(x=2\).
Giao điểm của parabol với trục tung là \(A\left(0;3\right)\), giao điểm của parabol với trục hoành là \(B\left(1;0\right)\) và \(C\left(3;0\right)\).
Điểm đối xứng với điểm \(A\left(0;3\right)\) qua trục đối xứng \(x=2\) là \(D\left(4;3\right)\).
Vẽ parabol qua các điểm được xác định như trên, ta được đồ thị hàm số \(y=x^2-4x+3\).
Nhận xét: Cho hàm số \(y=ax^2+bx+c\left(a\ne0\right)\)
| Với \(a>0\) | Với \(a< 0\) |
|
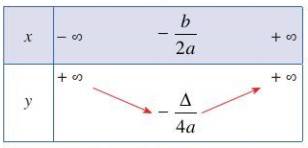
Hàm số nghịch biến trên khoảng \(\left(-\infty;-\dfrac{b}{2a}\right);\) Hàm số đồng biến trên khoảng \(\left(-\dfrac{b}{2a};+\infty\right);\) \(-\dfrac{\Delta}{4a}\) là giá trị nhỏ nhất của hàm số. Bảng biến thiên:
Hàm số có tập giá trị là \(T=[-\dfrac{\Delta}{4a};+\infty).\) |
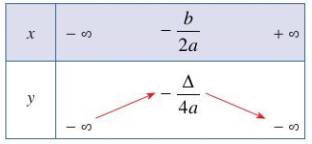
Hàm số đồng biến trên khoảng \(\left(-\infty;-\dfrac{b}{2a}\right);\) Hàm số nghịch biến trên khoảng \(\left(-\dfrac{b}{2a};+\infty\right);\) \(-\dfrac{\Delta}{4a}\) là giá trị lớn nhất của hàm số. Bảng biến thiên:
Hàm số có tập giá trị là \(T=(-\infty;-\dfrac{\Delta}{4a}].\) |
@200424190395@@200424192609@@200424284411@@200424415481@@200424481909@

Bạn có thể đánh giá bài học này ở đây