Bài học cùng chủ đề
- Tập hợp. Các phép toán trên tập hợp
- Tập hợp
- Tập hợp con. Hai tập hợp bằng nhau
- Các tập hợp số
- Giao của hai tập hợp
- Hợp của hai tập hợp
- Hiệu của hai tập hợp
- Bài toán chứa tham số
- Tập hợp, tập hợp con, tập hợp bằng nhau
- Phép toán hợp, giao, hiệu, phần bù trên tập hợp
- Các tập hợp số
- Các phép toán trên tập hợp số
- Bài toán tập hợp chứa tham số và bài toán ứng dụng thực tiễn
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
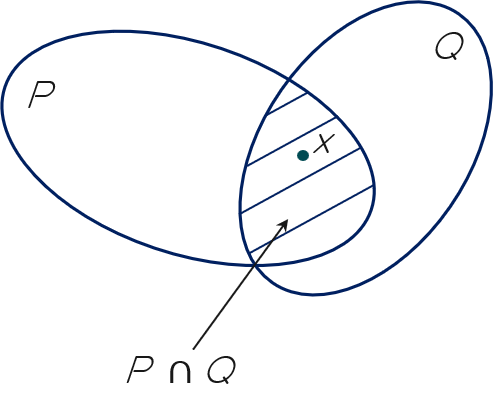
Nếu x∈P∩Q thì
x chỉ thuộc P.
x thuộc cả P và Q.
x chỉ thuộc Q.
x thuộc P hoặc x thuộc Q.
Câu 2 (1đ):
Giao của hai tập hợp C = {2 ; -3 ; 7 ; 12 ; 17} và K = {18 ; 11} là
{18 ; 11}.
{2 ; -3 ; 7 ; 12 ; 17 ; 18 ; 11}.
∅.
{12}.
Câu 3 (1đ):
Cho hai tập hợp M={x∈Nx là ước của 16} và H={x∈Nx là ước của 20}. Khẳng định nào sau đây đúng?
A
M={1;2;4;8;16} và H={1;2;4;5;10;20}.
B
M={1;2;4;8} và H={1;2;4;5;10}.
C
M={1;2;8;16} và H={1;2;5;10;20}.
D
M={2;4;8;16} và H={2;4;5;10;20}.
Câu 4 (1đ):
của 3 và 4.
Hoàn thành mệnh đề sau:
Nếu a vừa là bội của 3, vừa là bội của 4 thì a là
- bội chung
- bội chung nhỏ nhất
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- ở
- [âm nhạc]
- Hà Nội dung quan trọng tiếp theo ở trong
- bài số 2 này là các phép toán trên tập
- hợp
- với Chính tập hợp Chúng ta có các phép
- thần nào đó có phải là các phép cộng trừ
- nhân chia hai không thì các em sẽ cùng
- thầy tìm hiểu qua ví dụ sau đây bạn lớp
- trưởng có lên danh sách các thành viên
- trong lớp tham gia vào câu lạc bộ bóng
- rổ và câu lạc bộ bóng đá như sau các bạn
- Nam tham gia câu lạc bộ bóng rổ bao gồm
- có bạn nam Công Dũng quyết và Tuấn còn
- câu lạc bộ bóng đá thì có bạn Nam Tuấn
- Bình Long và Hùng tham gia biết trong
- lớp không có hai bạn nào trùng tên nhau
- vậy thì các em sẽ cho thầy biết có bao
- nhiêu bạn tham gia vào cả hai đội bóng
- Vừa tham gia đội bóng rổ và Vừa tham gia
- đội bóng đá thì quan sát và chồng sang
- sách này do không có hai bạn nào trúng
- tên nên Mình thấy bạn em và bạn Tuấn
- tham gia vào cả hai đội bóng vậy Nếu như
- thầy sử dụng biểu đồ venn để biểu diễn
- tập hợp các bạn tham gia vào hai câu lạc
- bộ này thấy gọi tập hợp các bạn tham gia
- câu lạc bộ bóng rổ là p còn quy là cuối
- cùng là bộ bóng đá vẫy thị có hai bạn
- tham gia cả hai đội bóng là nam và Tuấn
- nếu như chúng ta biểu diễn bằng sơ đồ
- venn thị Bắc Nam và bạn Tuấn vừa có mặt
- ở trong p và vừa có mặt ở trong quy hay
- nói theo ngôn ngữ của tập hợp thì nam và
- Tuấn là hai phần tử thuộc cả tập hợp P
- và tập hợp quy tập hợp gồm có Nam và
- Tuấn chính là sao của hai tập hợp cây và
- quy và phép toán đầu tiên chúng ta sẽ
- tìm hiểu ở trong phần các phép toán trên
- tập hợp đó là giao của hai tập hợp thế
- nào là giao của hai tập hợp tập hợp gồm
- tất cả các phần tử vừa thuộc vào P và
- vừa thuộc vào quy là giao của cây và quy
- khi a messy ký học giao của hai tập hợp
- A và quy là p dao quy như thế này kem
- chú ý vào ký hiệu giao và minh họa bằng
- sơ đồ venn như ở phần đầu của chúng ta
- thì P và Q sẽ có chung nhau một phần
- thầy sẽ gạch chéo phần đó và đó chỉ là
- tập hợp p giao quỹ
- phát từ khái niệm này kem sẽ hoàn thành
- chưa thấy mệnh đề tương đương sau đây
- ích thuộc vào tập hợp xây dựng đê khi và
- chỉ khi đáp án thứ nhất ích thuộc xây
- hoặc x thuộc đây phải đáp án thứ hai ích
- thuộc C và x thuộc D nếu như thay lấy
- một phần tử x thuộc vào tập hợp p giao
- cu Ken sẽ thấy
- chính xác X nằm trong p và x cũng nằm
- trong quy như vậy ích vừa thuộc p vừa
- thuộc quy do nó quay trở lại với mệnh đề
- tương đương này thì ít thuộc vào tập hợp
- C Giao Lê khi và chỉ khi ích thuộc xây
- và thủ tục đi ích đồng thời thuộc vào cả
- hai tập hợp đó nhất
- từ mạng để tương đương cũng như khái
- niệm này chúng ta có thể viết ngắn gọn
- giao của hai tập hợp như sau
- p.gia quy chính là tập hợp các giá trị x
- các phân tử X sao cho x thuộc P và x
- thuộc quy đó là giao của hai tập hợp và
- vận dụng kem sẽ trả lời ngay cho thầy
- câu hỏi đầu tiên cho 3 tập hợp là xây ca
- và Tây như kèm lòng quan sát được ở đây
- yêu cầu là xác định giao của tập hợp C
- với tập hợp cây và tập hợp ca dao với
- tập hợp C để xác định xây dao tay thì
- các em sẽ quan sát và tìm ra những phần
- tử vừa thuộc họ xây và vừa thuộc vào
- T2 thịt chị thuộc của xây -3 cũng chỉ
- thuộc họ xây bảy thì vừa tục xây vừa
- thuộc Tây 12 chỉ thuộc c17 vừa thuộc xây
- Mẹ
- con lại bên này chúng ta có âm hay ma
- 2018 thì chỉ thuộc vào Tây thôi Do Đỏ
- tập hợp C giáo t sẽ gồm có hai phần tử
- là 7 và 17 tương tự như thế với tập hợp
- ca dao xây
- chính xác không có phần tử nào mà vừa
- thuộc ca vừa dụng C do đó chúng ta sẽ
- kết luận k6c bằng tập rỗng thứ tự như
- thế với câu hỏi tiếp theo em sẽ tìm giao
- của hai tập hợp trong các trường hợp sau
- đây trường hợp đầu tiên với m là tập các
- số tự nhiên x sao cho x là ước của 16
- còn hát là tập các số tự nhiên x sao cho
- x là ước của 20 thì để tìm giao của hai
- tập hợp trên bước đầu tiên kem sẽ Liệt
- kê các phần tử của tập hợp m và tập hợp
- hát cho thời nhất
- ứng viên của 16 thì chúng ta sẽ có mơ
- gồm cổ 5 phần tử là 1248
- từ tương tự với hát chúng ta có các phần
- tử làm 1 2 4 5 10 và 20 vào nhìn ở dạng
- liệt kê Này khi các em sẽ thấy ngay được
- các phần tử chung của cả hai tập hợp là
- 1 2 và 4 khi đó mờ Giao hát chính là tập
- hợp các phần tử này như vậy Khi mà tập
- hợp m và H viết bằng cách chỉ ra tính
- chất đặc trưng thì các em sẽ chưa thấy
- được ngay các phần tử chung của hai tập
- hợp này khi đó chúng ta có thể nghĩ tới
- việc chuyển về dạng Liệt kê các phần tử
- để kèm Tìm các phần tử chung hai ngựa ở
- trong phần mở đầu chúng ta quan sát và
- sơ đồ venn để thấy được phần chung của
- cả hai tập hợp Tuy nhiên ở trong ký dụng
- trước hai ví dụ này thì kết quả giao của
- hai tập hợp là một tập hợp có thể là có
- Không phần tử tức là giật rỗng hoặc có
- hữu hạn thần tử
- Nhưng ở trong trường hợp mà sao là một
- tập hợp có vô hạn phần tử vô số phần tử
- Ừ thì chúng ta sẽ làm như thế nào trước
- khi đến với trường hợp đó thì kem sẽ
- nhận xe cho thầy Ở đây mờ dao hát tức là
- các giá trị ích sau giỏ ích vừa là ước
- của 16 và vừa là ước của 20
- khi đổ Mở giọng hát chính là tập hợp các
- ước chung của 16 và 20 và đây cũng là
- một cách khác để chúng ta tìm ra giao
- của hai tập hợp này và cũng với ý tưởng
- tương tự như thế trong trường hợp mà một
- tập hợp có vô số phần tử chúng ta không
- thể liệt kê hết tất cả các phần tử của
- tập hợp đó ví dụ như E gồm các số tự
- nhiên là bộ của ba cũng như ép là các số
- tự nhiên là bộ của bốn Đây là các tập
- hợp có vô số phần tử khi chúng ta sẽ đi
- tìm dao của chủ nghĩa sau giao của s sẽ
- chỉ là các số tự nhiên mà vừa là bội của
- ba và vừa là bội của 4
- chính là tập hợp các số tự nhiên x sao
- cho x là bộ chung của 3 và 4 và giao củ
- I II và s cũng là một tập hợp mà có vô
- số phần tử như vậy trong phép toán đầu
- tiên trên tập hợp là phép toán giao kem
- năm cho thấy Khái niệm và cách xác định
- giao của hai tập hợp trong các trường
- hợp nếu như trong trường hợp có hữu hạn
- thành từ thì các em có thể viết dưới
- dạng liệt kê hoặc là sơ đồ venn để nhìn
- những phần tử vừa thuộc tập hợp này vừa
- thuộc tập hợp kia con Nếu như trong
- trường hợp của vô số phần tử nhựa ở ví
- dụ này kem có thể để ở dạng tính chất
- đặc trưng hoa trong phần sau khi kem đã
- tìm hiểu một số tập con thường dùng của
- tập số thực r ta sẽ tiếp tục đề cập tới
- giao của hai tập hợp
- ờ ờ
OLMc◯2022


Bạn có thể đánh giá bài học này ở đây