Giá trị lượng giác của một góc từ 0 độ đến 180 độ SVIP

I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ \(0^\circ\) ĐẾN \(180^\circ\)

Trong mặt phẳng tọa độ \(Oxy\), nửa đường tròn tâm \(O\), bán kính \(R=1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.

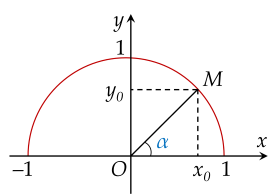
Với mỗi góc \(\alpha\),  \(0^\circ\leq \alpha\leq 180^\circ\), ta xác định duy nhất một điểm \(M\left(x_0;y_0\right)\) trên nửa đường tròn đơn vị sao cho \(\widehat{xOM}=\alpha\). Khi đó:

• ​\(\sin\) của góc \(\alpha\), kí hiệu là \(\sin\alpha\), được xác định bởi \(\sin\alpha=y_0\).
• ​\(côsin\) của góc \(\alpha\), kí hiệu là \(\cos\alpha\), được xác định bởi \(\cos\alpha=x_0\).
• ​\(tang\) của góc \(\alpha\), kí hiệu là \(\tan\alpha\) , được xác định bởi \(tan\alpha=\dfrac{y_0}{x_0}\)(\(x_0\ne0\)).
• ​\(côtang\) của góc \(\alpha\), kí hiệu là \(\cot\alpha\), được xác định bởi \(\cot\alpha=\dfrac{x_0}{y_0}\)\(\left(y_0\ne 0\right)\).

Các số \(\sin\alpha,\cos\alpha,\tan\alpha,\cot\alpha\) được gọi là giá trị lượng giác của góc \(\alpha\).

Chú ý.

• \(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}\left(\alpha\ne90^0\right);\) \(\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}\left(0^\circ< \alpha< 180^\circ\right).\)
• ​\(\sin\left(90^\circ-\alpha\right)=\cos\alpha\left(0^\circ\le\alpha\le90^\circ\right)\);

\(\cos \left(90^\circ-\alpha \right)=\sin \alpha \left(0^\circ\le \alpha \le 90^\circ\right)\);

\(\tan \left(90^\circ-\alpha \right)=\cot \alpha \left(0^\circ< \alpha \le 90^\circ\right)\);

\(\cot \left(90^\circ-\alpha \right)=\tan \alpha \left(0^\circ\le \alpha < 90^\circ\right)\).

Với \(0^\circ\le\alpha\le180^\circ\) thì:

\(\sin \left (180^\circ-\alpha\right )=\sin\alpha \),

\(\cos \left (180^\circ-\alpha\right )=-\cos\alpha \),

\(\tan \left (180^\circ-\alpha\right )=-\tan\alpha \left ( \alpha \neq 90^\circ\right )\),

\(\cot \left (180^\circ-\alpha\right )=-\cot\alpha\left ( 0^\circ< \alpha < 180^\circ \right )\).

Ví dụ.

$\sin 150^\circ = \sin (180^\circ - 30^\circ) = \sin 30^\circ = \dfrac{1}{2}$.

$\tan 120^\circ = \tan (180^\circ - 60^\circ) = -\tan 60^\circ = \sqrt{3}$.

⚡Bảng giá trị lượng giác của một số góc đặc biệt

⚡ Ta có thể sử dụng máy tính cầm tay để tính (đúng hoặc gần đúng) các giá trị lượng giác của một góc và tính góc khi biết giá trị lượng giác của góc đó.

Chẳng hạn, với một loại máy tính cầm tay, sau khi mở máy tính ta bấm phím:   (SET- UP) rồi bấm phím  để chọn đơn vị đo "độ"

• Tính giá trị lượng giác của một số góc

•   Tìm góc khi biết một giá trị lượng giác của góc đó

Chú ý. ​

• Khi tìm $x$, biết $\sin x$, máy tính chỉ đưa ra giá trị $x \le 90^\circ$
• Muốn tìm $x$ khi biết $\cos x$, $\tan x$, ta cũng làm tương tự như trên, chỉ thay phím  tương ứng bởi phím , .

II. ĐỊNH LÍ CÔSIN 

Cho tam giác \(ABC\) có \(BC=a,CA=b,AB=c.\) Khi đó:

\(a^{^{ }2}=b^2+c^2-2bc\cos A,\)

\(b^{^{ }2}=c^2+a^2-2ca\cos B,\)

\(c^{^{ }2}=a^2+b^2-2ab\cos C\).

Hệ quả.

\(\cos A=\frac{b^2+c^2-a^2}{2bc}\);

\(\cos B=\frac{c^2+a^2-b^2}{2ca}\);

\(\cos C=\frac{a^2+b^2-c^2}{2ab}\).

Ví dụ: Cho tam giác \(ABC\) có các cạnh \(AC=10\) cm, \(BC=16\) cm và góc \(C\) bằng \(110^\circ\). Tính cạnh \(AB\) và góc \(A\) của tam giác đó.

Giải

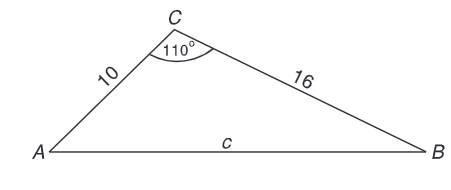
Theo định lí côsin ta có:

 \(AB^2=CA^2+CB^2-2CA.CB.\cos\widehat{C}\)

\(AB^2=16^2+10^2-2.16.10\)\(\cos110^\circ\)

\(AB^2\approx465,44\)

suy ra \(AB\approx\sqrt{465,44}\approx21,6\) (cm).

Theo hệ quả định lí côsin, ta có:

\(\cos A=\dfrac{AB^2+AC^2-BC^2}{2.AB.AC}\)

\(\cos A\approx \frac{10^2+\left(21,6\right)^2-16^2}{2.10.21,6}\approx 0,72\)

suy ra \(A\approx\) \(43^\circ56'\).

III. ĐỊNH LÍ SIN

Cho tam giác \(ABC\) có \(BC=a,CA=b,AB=c\) và bán kính đường tròn ngoại tiếp bằng \(R\). Khi đó:

\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\)

Ví dụ. Cho tam giác \(ABC\) có \(AB=6\) cm, \(\widehat{B}=30^\circ,\widehat{C}=45^\circ\), tính độ dài cạnh \(AC\) và bán kính đường tròn ngoại tiếp tam giác \(ABC.\)

Giải

Áp dụng định lí sin trong tam giác \(ABC\) ta có:

\(\dfrac{AC}{\sin B}=\dfrac{AB}{\sin C}\Rightarrow AC=\dfrac{AB.\sin B}{\sin C}=\dfrac{6.\sin30^\circ}{\sin45^\circ}\approx4,24\) cm.

Ta lại có 

\(\dfrac{AB}{\sin C}=2R\Rightarrow R=\dfrac{AB}{2.\sin C}=\dfrac{6}{2.\sin45^\circ}\approx4,24\) cm.