Bài học cùng chủ đề
- Mở đầu về đường tròn
- Đường tròn
- Tính đối xứng của đường tròn
- Dây và đường kính của đường tròn
- Xác định vị trí tương đối của điểm với đường tròn
- So sánh độ dài đoạn thẳng
- Đường tròn và tính đối xứng của đường tròn
- Chứng minh các điểm cùng thuộc một đường tròn
- Xác định vị trí tương đối của hai đường tròn
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đường tròn và tính đối xứng của đường tròn SVIP
Cho đường tròn $(O;2$ cm$)$ và $(A;2$ cm$)$ cắt nhau tại $C$, $D$ điểm $A$ nằm trên đường tròn tâm $O$.
a) Vẽ đường tròn $(C;2$ cm$)$.
b) Đường tròn $(C;2$ cm$)$ có đi qua hai điểm $O$ và $A$ hay không? Vì sao?
Hướng dẫn giải:
a) Vẽ đường tròn $(C;2$ cm$)$
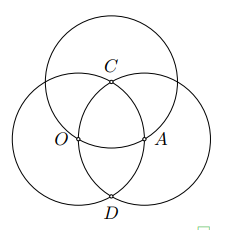
b) Đường tròn $(O;2$ cm$)$ và $(A;2$ cm$)$ cắt nhau tại $C$, $D$, điểm $A$ nằm trên đường tròn tâm $O$ nên:
$OC=OD=2$ cm, $AC=AD=2$ cm.
Suy ra $OC=CA=2$ cm.
Do đó đường tròn $(C;2$ cm$)$ đi qua hai điểm $O$ và $A$.
Cho đường tròn $\left(O;R \right)$ và dây $AB$ khác đường kính. Gọi $M$ là trung điểm của $AB$.
a) Đường thẳng $OM$ có phải là đường trung trực của đoạn thẳng $AB$ hay không? Vì sao?
b) Tính khoảng cách từ điểm $O$ đến đường thẳng $AB$, biết $R=5$ cm, $AB=8$ cm.
Hướng dẫn giải:
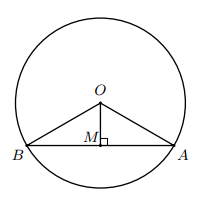
a) Ta có $\Delta OAB$ cân tại $O$ vì $OA=OB=R$.
Mà $M$ là trung điểm của $AB$ nên $OM$ là đường trung tuyến của tam giác $OAB$.
Khi đó $OM$ cũng là đường trung trực của đoạn thẳng $AB$.
b) Khoảng cách từ điểm $O$ đến đường thẳng $AB$ chính là đoạn thẳng $OM$.
$M$ là trung điểm của $AB$ nên $AM=\dfrac{AB}{2}=4$ cm.
Xét $\Delta OAM$ vuông tại $M$, có $O{{A}^{2}}=A{{M}^{2}}+O{{M}^{2}}$ (định lí Pythagore).
Suy ra $OM=\sqrt{OA^2-AM^2}=\sqrt{5^2-4^2}=3$ cm.
Cho tam giác $ABC$, cạnh $BC$ cố định, $AB=4$ cm.
a) Điểm $A$ di động trên đường nào?
b) Trung điểm $M$ của $AC$ di động trên đường nào?
Hướng dẫn giải:
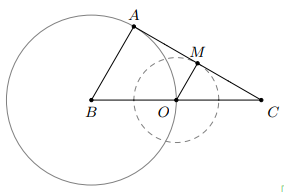
a) Điểm $B$ cố định. Điểm $A$ cách $B$ một khoảng là $4$ cm nên $A$ nằm trên đường tròn $(B;4$ cm$)$.
b) Gọi $O$ là trung điểm của $BC$ thì $O$ là một điểm cố định.
Ta có $OM=\dfrac{1}{2}AB=2$ cm.
Điểm $M$ cách điểm $O$ một khoảng $2$ cm nên $M$ nằm trên đường tròn $(O;2$ cm$)$.
Cho điểm $M$ nằm trên đường tròn $(O)$ đường kính $AB$. Sử dụng tính đối xứng của đường tròn $(O)$, nêu cách tìm:
a) Điểm $N$ đối xứng với điểm $M$ qua tâm $O$.
b) Điểm $P$ đối xứng với điểm $M$ qua đường thẳng $AB$.
Hướng dẫn giải:
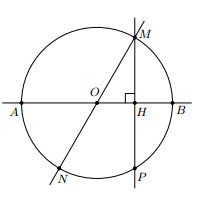
a) Do $O$ là tâm đối xứng của $(O)$ nên điểm $N$ đối xứng với điểm $M$ qua tâm $O$ phải vừa thuộc $OM$, vừa thuộc $\left(O \right)$.
Vậy $N$ là giao điểm của đường thẳng $OM$ với $(O)$.
b) Do $AB$ là trục đối xứng của $(O)$ nên điểm $P$ đối xứng với điểm $M$ qua $AB$ phải vừa thuộc $(O)$, vừa thuộc đường thẳng vuông góc hạ từ $M$ xuống $AB$.
Vậy $P$ là giao điểm của $(O)$ với đường thẳng đi qua $M$ và vuông góc với $AB$.
Cho hai đường tròn $(A; 6$ cm$)$ và $(B;4$ cm$)$ cắt nhau tại $C$ và $D$, $AB=8$ cm. Gọi $I$, $K$ lần lượt là giao điểm của hai đường tròn đã cho với đoạn thẳng $AB$.
a) Tính độ dài của các đoạn thẳng $CA$, $CB$, $DA$ và $DB$.
b) Điểm $I$ có phải là trung điểm của đoạn thẳng $AB$ không?
c) Tính độ dài của đoạn thẳng $IK$.
Hướng dẫn giải:
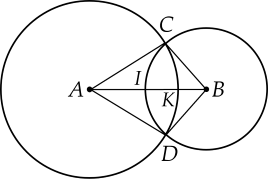
a) Hai đường tròn $(A; 6$ cm$)$ và $(B;4$ cm$)$ cắt nhau tại $C$ và $D$ nên $AC=AD=6$ cm, $BC=BD=4$ cm.
b) $AB=8$ cm, $BC=BD=BI=4$ cm.
Suy ra $AI=AB-IB=8-4=4$ cm.
Điểm $I$ là trung điểm của đoạn thẳng $AB$.
c) Ta có: $AK=AC=6$ cm nên $IK=AK-AI=6-4=2$ cm.
Cho hình chữ nhật $ABCD$ có $AD=18$ cm và $CD=12$ cm. Chứng minh rằng bốn điểm $A$, $B$, $C$, $D$ cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Hướng dẫn giải:
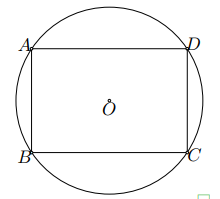
Ta có $ABCD$ là hình chữ nhật nên $OA=OB=OC=OD$, suy ra các điểm $A$, $B$, $C$, $D$ nằm trên một đường tròn tâm $O$.
Tam giác $ABC$ vuông tại $B$ có: $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{6}^{2}}+{{9}^{2}}}=\sqrt{117}$.
Vậy bán kính $R=\dfrac{AC}{2}=\dfrac{\sqrt{117}}{2}$.
Cho hai đường tròn cùng tâm $\left(O;R \right)$, $\left(O;r \right)$ với $R>r$. Các điểm $A$, $B$ thuộc đường tròn $\left(O;R \right)$, các điểm ${A}'$, ${B}'$ thuộc đường tròn $\left(O;r \right)$ sao cho $O$, $A$, ${A}'$ thẳng hàng; $O,B,{B}'$ thẳng hàng và điểm $O$ không thuộc đường thẳng $AB$. Chứng minh:
a) $\dfrac{O{A}'}{OA}=\dfrac{O{B}'}{OB}$.
b) $AB$ // ${A}'{B}'$.
Hướng dẫn giải:
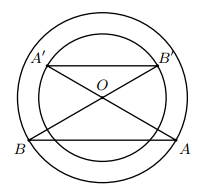
a) Từ giả thiết, ta có $\dfrac{O{A}'}{OA}=\dfrac{r}{{{R}'}}$;
$\dfrac{O{B}'}{OB}=\dfrac{r}{{{R}'}}$.
Suy ra $\dfrac{O{A}'}{OA}=\dfrac{O{B}'}{OB}$.
b) Vì $\dfrac{O{A}'}{OA}=\dfrac{O{B}'}{OB}$ nên theo hệ quả của định lí Thalès ta có:
$AB$ // ${A}'{B}'$.
Cho đường tròn tâm $\left(O \right)$, đường kính $AB$ và một dây $AC$ bằng bán kính đường tròn. Tính các góc của $\Delta ABC$.
Hướng dẫn giải:
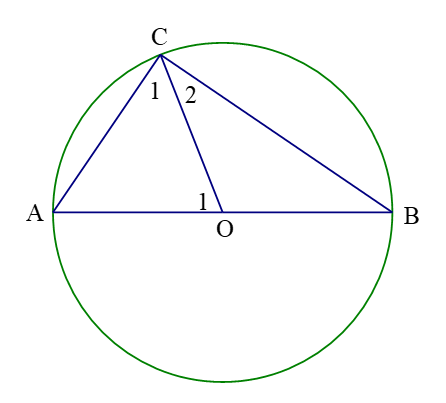
Tam giác $OAC$ có ba cạnh bằng nhau $\left(AC=OA=OC \right)$ nên là tam giác đều
Suy ra $ \widehat{A}=\widehat{C_1}=\widehat{O_1}=60^\circ$.
Ta có: $OAC$ có $OB=OC$ nên cân tại $O$ suy ra $\widehat{B}=\widehat{C_2}$;
$\widehat{O_1}$ là góc ngoài của $\Delta OBC$.
Do đó $\widehat{O_1}=\widehat{B}+\widehat{C_2}=2\widehat{B}=2\widehat{C_2}$
$\widehat{B}=\widehat{C_2}=\dfrac{1}{2}\widehat{O_1}=30^\circ$
$\widehat{ACB}=\widehat{C_1}+\widehat{C_2}=90^\circ$
Vậy $\widehat{A}=60^\circ; \, \widehat{B}=30^\circ; \, \widehat{C}=90^\circ$.
$\Delta CAB$ có trung tuyến $CO$ bằng nửa cạnh đối xứng $AB$ nên vuông tại $C$ với $\widehat{ACB}=90^\circ$
Suy ra $\widehat{A}=60^\circ$ và $\widehat{B}=30^\circ$
Vậy $\Delta ABC$ có $\widehat{C}=90^\circ; \, \widehat{A}=60^\circ; \, \widehat{B}=30^\circ$.
