Bài học cùng chủ đề
- Diện tích xung quanh và thể tích của hình chóp
- Diện tích xung quanh và thể tích của hình chóp tam giác đều
- Diện tích xung quanh và thể tích của hình chóp tứ giác đều
- Diện tích xung quanh của hình chóp tam giác đều
- Thể tích hình chóp tam giác đều
- Diện tích xung quanh của hình chóp tứ giác đều
- Thể tích hình chóp tứ giác đều
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
1. ĐỊNH NGHĨA
Hình chóp S.ABCD có:
+ đáy ABCD là hình vuông;
+ các mặt bên là những tam giác cân bằng nhau, có chung đỉnh.
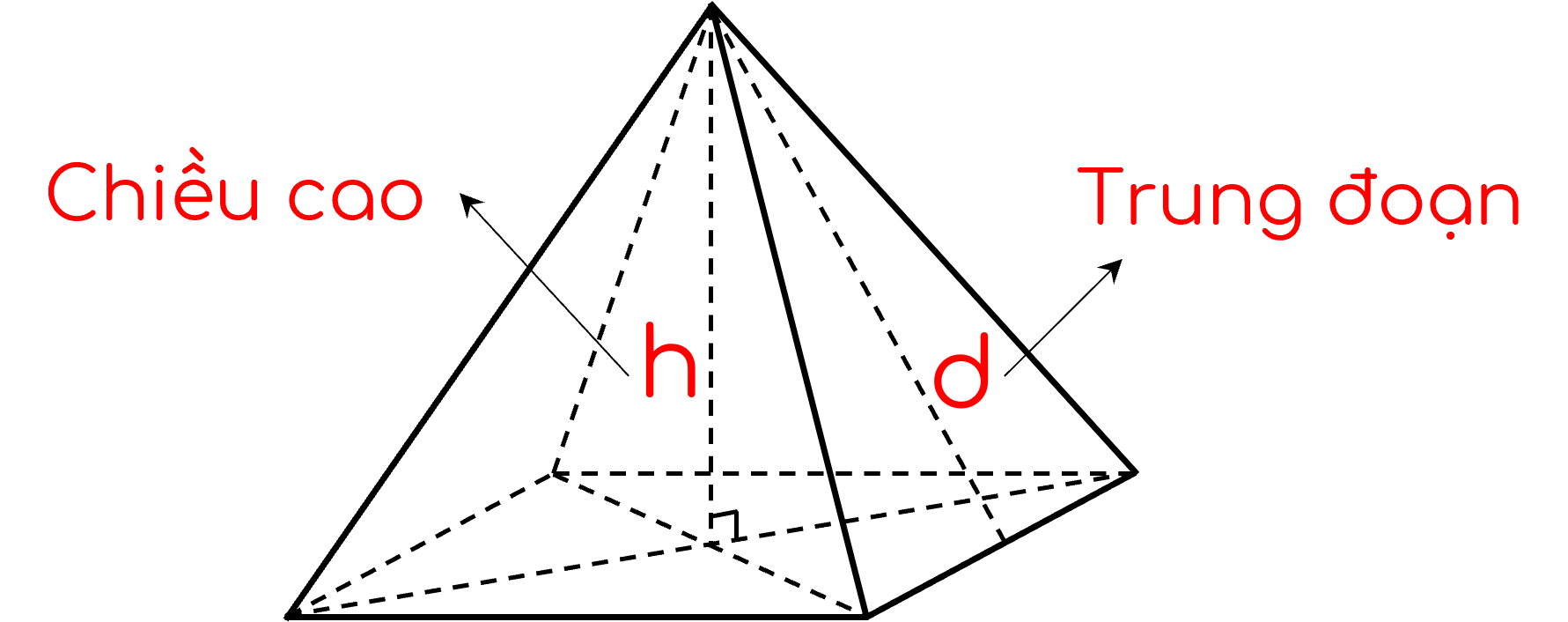
2. CÔNG THỨC
+ Diện tích xung quanh: $S_{xq} = p . d$.
+ Thể tích: $V = \dfrac13.S. h$.
Trong đó, $p$: nửa chu vi đáy.
Cho hình chóp tứ giác đều S.ABCD có nửa chu vi 12 cm như hình vẽ.
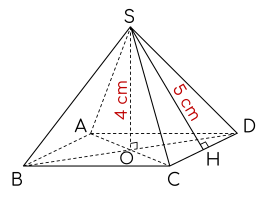
Diện tích xung quanh của hình chóp tứ giác đều trên là
Diện tích đáy của hình chóp tứ giác đều S.ABCD bằng
Diện tích xung quanh của hình chóp tứ giác đều có các kích thước như hình vẽ bằng
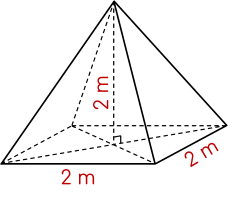
Thể tích của hình chóp tứ giác đều có kích thước như hình vẽ trên là
Kim tự tháp Kheops ở Ai Cập được xây dựng vào khoảng 2 500 năm trước Công nguyên. Đây là một trong những công trình cổ nhất và duy nhất còn tồn tại trong số 7 kì quan thế giới cổ đại. Kim tự tháp này có dạng hình chóp tứ giác đều cao 147 m, cạnh đáy dài 230 m. Kim tự tháp Kheops có thể tích bằng bao nhiêu?
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- [âm nhạc]
- [âm nhạc]
- Chào mừng các em đã quay trở lại với
- khóa học Toán lớp 8 trên trang on.vn
- phần thứ hai của bài học hình chóp từ
- giác đều chúng ta sẽ đi tìm hiểu công
- thức tính diện tích xung quanh và thể
- tích của nó nhé Vậy chúng ta sẽ bắt đầu
- luôn với hai loại công thức này Đầu tiên
- là diện tích xung quanh của hình chóp tứ
- giác đều
- với hình chóp tứ giác đều có cạnh đáy
- bằng a
- Trung đoạn độ dài đây thì diện tích xung
- quanh sẽ bằng tích của nửa chu vi đáy
- với trung đoạn
- đáy là hình vuông thì nửa chu vi đáy sẽ
- là p = 2A nhân với trung đoạn D ta có
- công thức diện tích xung quanh s xung
- quanh bằng p nhìn đi trong đó P là nửa
- chu vi đáy đây là độ dài Trung đoạn
- việc ghi nhớ thì không khó khăn bởi vì
- công thức tính diện tích xung quanh này
- cũng giống như ở bài hình chóp tam giác
- đều thôi ta vẫn lấy nửa chu vi đáy nhân
- với trung đoạn chỉ khác nhau là nửa chu
- vi đáy ở đây ở hình chóp tứ giác đều thì
- tính bằng của công thức khác thôi
- còn thể tích của hình chóp tứ giác đều
- thì cũng bằng 1/3 tích của diện tích mặt
- đáy với chiều cao của nó như trong hình
- vẽ này
- ta sẽ có đáy là hình vuông cạnh a thì
- diện tích sẽ là a bình phương chiều cao
- bằng h
- v = 1/3 s nhân h trong đó s là diện tích
- đáy H là chiều cao của hình chóp và công
- thức thể tích thì cũng giống hình chóp
- tam giác đều thôi vẫn là v = 1 phần 3 SH
- như vậy những việc ghi nhớ hay công thức
- này là không hề khó khăn diện tích xung
- quanh thì bằng nửa chu vi đáy nhân với
- độ dài Trung đoạn thể tích thì bằng 1/3
- diện tích đáy nhân với chiều cao để
- chúng ta áp dụng ngay vào trong các câu
- hỏi hỏi chấm 1 yêu cầu tính diện tích
- xung quanh và thể tích của hình chóp tứ
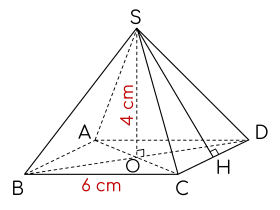
- giác đều SABCD biết rằng độ dài cạnh đáy
- là 6 cm
- chiều cao bằng 4 cm và Trung đoạn bằng 5
- cm
- thì bài này đơn giản là thấy áp dụng
- công thức thôi
- diện tích xung quanh sẽ bằng nửa chu vi
- đáy nhân với trung đoạn khi đáy là hình
- vuông chu vi sẽ là 4 nhân với độ dài một
- cạnh vậy nửa chu vi đáy ABCD sẽ là 4 x 6
- và chia 2 bằng 12 cm Vậy diện tích xung
- quanh
- chính xác diện tích thông minh Quỳnh
- chóp từ ra đều SABCD sẽ được tính theo
- công thức p nhân d thì bằng 12 D Chú ý
- Trung đoạn nha Thì độ dài bằng 5 12 x 5
- = 60 đơn vị cm2
- tương tự như vậy các bạn tính cho thầy
- thể tích của hình chóp tứ giác đều này
- nhé
- và trước tiên chúng ta phải tính được
- diện tích đáy rồi
- chính xác diện tích đáy ABCD sẽ là a
- bình phương độ dài một cạnh bình phương
- f sẽ bằng 36 đơn vị cm2 thi thể tích p =
- 1/3 diện tích đáy là s nhân với chiều
- cao là h f ta tính được bằng 36 này
- chiều cao thì bằng 4 như vậy 1/3 nhân 36
- nhân 4 36 chia 3 được 12 nhân 4 ta được
- 48 và đơn vị cm khối nhé
- như vậy qua hỏi chấm 1 chúng ta đã vận
- dụng được công thức tính diện tích xung
- quanh này thể tích của hình chóp tứ giác
- đều rồi
- tương tự như thế các bạn sẽ áp dụng vào
- trong hỏi chấm 2 với một bài toán thực
- tế bóc đô muốn là một chiếc hộp gỗ có
- hình dạng chóp tứ giác đều như thế này
- với độ dài cạnh đáy là 2 m Trung đoạn là
- 3m và Bắc Đô muốn sơn 4 mắt xung quanh
- của hộp gỗ biết rằng cứ mỗi mét vuông
- Sơn sẽ cần phải trả 30.000 đồng cả tiền
- sơn và tiền công Vậy thì bác đù sẽ phải
- trả chi phí bao nhiêu để sơn chiếc hộp
- gỗ của dạng hình chóp mà chúng ta vừa đề
- cập như vậy Bài toán này là phải tính
- được diện tích của bốn mặt mà diện tích
- 4 mặt xung quanh của hình hộp gỗ chính
- là diện tích xung quanh của hình chóp tứ
- giác đều cho nên ta phải tính diện tích
- xung quanh trước đã
- chính xác rồi ở công ty nửa chu vi đáy
- sẽ là 4 nhân với 2 và chia 2 còn Trung
- đoạn là 3 quả 3 x 4 ta được 12 đơn vị
- mét vuông
- mà cứ mỗi mét vuông chi phí 30.000 vậy
- 12 mét vuông thì số tiền Bắc Đô phải trả
- sẽ là 12 nhân 30.000 bằng 360.000 đồng
- nhé
- hỏi chấm 2 thì ta áp dụng công thức tính
- diện tích xung quanh và các bạn cũng ghi
- nhớ cho thầy này diện tích xung quanh
- của một hình chóp tứ giác đều hay tam
- giác đều cũng vậy sẽ bằng tổng diện tích
- Các mặt bên Cho tam giác đều thì có 3
- mặt bên Cho tứ giác đều thì có 4 mặt bên
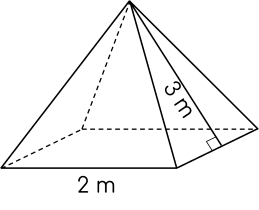
- còn trong câu hỏi tiếp theo một chiếc
- lều có dạng hình chóp tứ giác đều cạnh
- đáy bằng 2 m chiều cao cũng bằng 2 mét
- luôn yêu cầu tính thể tích không khí ở
- trong lều là bao nhiêu ở đây minh họa
- thôi lều này tất nhiên là sẽ phải buông
- phần rèm xuống nó sẽ có hình dạng của
- một hình chóp tứ giác đều hoàn chỉnh và
- yêu cầu tính thể tích bên trong của lều
- chính là thể tích của hình chóp tứ giác
- đều này
- nhắc lại cho các bạn cùng thức này thể
- tích thì bằng 1/3 diện tích đáy nhân với
- chiều cao chiều cao thì đề bài đã cho
- vậy ta cần tính diện tích đáy để tính
- được thể tích này diện tích đáy hay
- chính là diện tích nền của lều ấy ta áp
- dụng công thức tính diện tích hình vuông
- 2 nhân 2 2 bình phương bằng 4 đơn vị mét
- vuông
- chiều cao đề bài đã cho bằng 2m thì ta
- áp dụng công thức tính thể tích thể tích
- không khí trong lều v sẽ bằng 1/3 diện
- tích đáy là 4 nhân chiều cao là 2 kết
- quả là 8/3 đơn vị là mét khối nhất trong
- hỏi chấm 3 thì ta lại áp dụng công thức
- tính thể tích ở đó có bạn chú ý nếu bài
- toán mà chỉ cho mình hỏi bằng lời chưa
- thể hình dung ngay được hình vẽ và ta
- phải áp dụng công thức này thế nào ấy
- thì các bạn nên vẽ cho thầy vẽ vào vở
- hoặc vẽ ra nháp hình ảnh của một hình
- chóp tam giác đều hình Cho tứ giác đều
- và liệt kê các yếu tố về độ dài như là
- độ dài cạnh đáy và chiều cao mà đề bài
- đã cho để từ đó áp dụng vào công thức
- cho chính xác nhất vậy bây giờ quay trở
- lại với câu hỏi mở đầu kim tự tháp kéo
- có hình dạng hình chóp tứ giác đều cao
- 147m cạnh đáy là 230m thì thể tích bằng
- bao nhiêu
- công thức v = 1/3 f nhân h thì ta sẽ
- tính diện tích đáy trước
- đáy là hình vuông cạnh 230m thì diện
- tích là 230 bình phương đơn vị mét vuông
- chính xác rồi p = 1/3x nhân h
- cao 147 thì H9 bằng 147 thay số 1/3 nhân
- 230 bình phương nhân 147 thể tích là
- 2.592.100 mét khối thì các bạn có thể
- tưởng tượng được Sự đồ sộ của kim tự
- tháp Kê Úc là như thế nào và câu hỏi mở
- đầu cũng đã kết thúc cho bài học ngày
- nay của chúng ta các bạn cần ghi nhớ cho
- thầy định nghĩa này và hai công thức
- tính diện tích xung quanh cũng như thể
- tích của hình chóp tứ giác đều là j thầy
- Cảm ơn sự theo dõi của các em hẹn gặp
- lại các em trong các bài học tiếp theo
- trên online nhé


Bạn có thể đánh giá bài học này ở đây