Đáp án đề tuyển sinh vào lớp 10 thành phố Hà Nội năm 2021 - 2022 SVIP

Hướng dẫn giải:

1) Thay $x=16$ (TMĐK) vào biểu thức $A$, ta được:

$A=\dfrac{\sqrt{16}}{\sqrt{16}+3}=\dfrac{4}{7}$.

2) Chứng minh $A+B=\dfrac{3}{\sqrt{x}+3}$.

$A+B=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2 \sqrt{x}}{\sqrt{x}-3}-\dfrac{3 x+9}{x-9}=\dfrac{x-3 \sqrt{x}+2 x+6 \sqrt{x}-3 x-9}{(\sqrt{x}+3)(\sqrt{x}-3)}$

$=\dfrac{3(\sqrt{x}-3)}{(\sqrt{x}+3)(\sqrt{x}-3)}=\dfrac{3}{\sqrt{x}+3}$.

Hướng dẫn giải:

1) Gọi số bộ đồ bảo hộ y tế mà tổ sản xuất phải làm trong một ngày theo kế hoạch là $x$ (bộ), $(x>0)$.

Theo giả thiết ta có phương trình $\dfrac{4800}{x}-\dfrac{4800}{x+100}=8$

$\Leftrightarrow x^{2}+100 x-60000=0$ (vì $x>0$ ).

Giải phương trình tìm được $x=-300$ hoặc $x=200$.

Đối chiếu điều kiện và thử lại thấy $x=200$ thỏa mãn.

Vậy theo kế hoạch, mỗi ngày tổ sản xuất phải làm $200$ bộ đồ bảo hộ y tế.

2) Tính diện tích bề măt được sơn của thùng nước.

Diện tích bề mặt được sơn là diện tích xung quanh của thùng nước:

   $S=2 \pi R h \approx 2 . 3.14 . 0,5 . 1,6=5,024$ (m$^2$).

Vậy diện tích bề mặt được sơn của thùng nước xấp xỉ bằng $5,024$ m$^2$.

Hướng dẫn giải:

1) ĐKXĐ: $x \neq-1$.

$\left\{\begin{aligned}&\dfrac{3}{x+1}-2 y=-1 \\ &\dfrac{5}{x+1}+3 y=11\end{aligned} \Leftrightarrow\left\{\begin{aligned}&\dfrac{19}{x+1}=19 \\ &\dfrac{10}{x+1}+6 y=22\end{aligned} \Leftrightarrow\left\{\begin{aligned}&x+1=1 \\ &10+6 y=22\end{aligned} \Leftrightarrow\left\{\begin{aligned}&x=0 \\ &y=2\end{aligned} .\right.\right.\right.\right.$

Đối chiếu điều kiện và kết luận nghiệm của hệ phương trình là $(x ; y)=(0 ; 2)$.

2) Tìm $m$ để $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $\left|x_{1}-x_{2}\right|=2$.

Phương trình hoành độ giao điểm của đường thẳng $(d)$ và parabol $(P)$: $x^{2}=2 x+m-2 \Leftrightarrow x^{2}-2 x-m+2=0$ (1).

Đường thẳng $(d)$ cắt $(P)$ tại hai điểm phân biệt $\Leftrightarrow$ (1) có hai nghiệm phân biệt $\Leftrightarrow \Delta'>0 \Leftrightarrow m-1>0 \Leftrightarrow m>1 .$

Áp dụng định lý Vi-et, có: $\left\{\begin{aligned}&x_{1}+x_{2}=2 \\& x_{1} x_{2}=-m+2\end{aligned}\right.$ (*)

Biển đổi $\left|x_{1}-x_{2}\right|=2 \Leftrightarrow\left(x_{1}-x_{2}\right)^{2}=4 \Leftrightarrow\left(x_{1}+x_{2}\right)^{2}-4 x_{1} x_{2}=4$.

Từ (*) ta có: $4-4(-m+2)=4 \Leftrightarrow m=2$ (tm).

Kết luận $m=2$.

Hướng dẫn giải:

1)

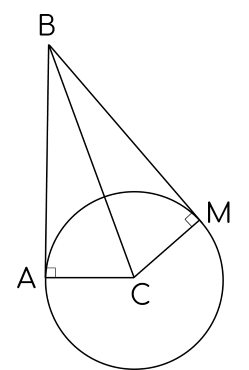
Tam giác $A B C$ vuông tại $A$ nên $\widehat{B A C}=90^{\circ}$

$\Rightarrow A$ thuộc đường tròn đường kính $B C$.

$B M$ là tiếp tuyến của đường tròn $(C)$ nên $\widehat{B M C}=90^{\circ} \Rightarrow M$ thuộc đường tròn đường kính $B C$.

Vậy bốn điểm $A$, $C, M$ và $B$ cùng thuộc đường tròn đường kính $B C$.

2)

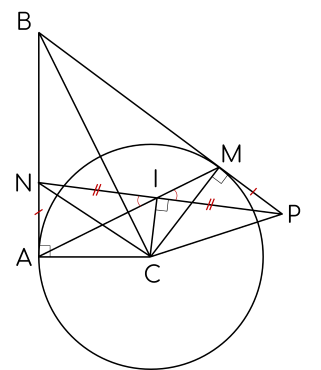
Xét $\triangle C A N$ và $\triangle C M P$ có:

   $C A=C M$;

   $\widehat{C A N}=\widehat{C M P}=90^{\circ}$;

   $A N=M P$

$\Rightarrow \triangle C A N=\Delta C M P$ (c.g.c)

$\Rightarrow C N=C P$.

$\Rightarrow$ Tam giác $C P N$ cân tại $C$.

Gọi $I$ là trung điểm của đoạn thẳng $N P$.

$\triangle C P N$ cân tại $C$ và $I$ là trung điểm của đoạn thẳng $N P$ nên $C I \perp N P$.

Tứ giác $N A C I$ nội tiếp $\Rightarrow \widehat{N I A}=\widehat{N C A}$.

Tứ giác $C I M P$ nội tiếp $\Rightarrow \widehat{M I P}=\widehat{M C P}$.

$\triangle C A N=\triangle C M P \Rightarrow \widehat{N C A}=\widehat{M C P}$.

Ta có $\widehat{N I A}+\widehat{P I A}=180^{\circ}$ (vì $I$ nằm giữa $N$ và $P$ )

$\Rightarrow \widehat{M I P}+\widehat{P I A}=180^{\circ}$.

Mà hai góc này kề nhau $\Rightarrow A, I, M$ là ba điểm thẳng hàng.

Vậy đường thẳng $AM$ đi qua trung điểm của đoạn thẳng $N P$.

Hướng dẫn giải:

Từ điều kiện $a^{2}+b^{2}=2$, ta có $(a+b)^{2}-2ab=2 \Rightarrow a b=\dfrac{1}{2}(a+b)^{2}-1$.

Đặt $x=a+b$.

Khi đó $P=3 x+\dfrac{1}{2} x^{2}-1=\dfrac{1}{2}(x+3)^{2}-\dfrac{11}{2}$.

Ta có $(a+b)^{2} \leq 2\left(a^{2}+b^{2}\right) \Rightarrow x^{2} \leq 4 \Rightarrow-2 \leq x \leq 2$.

Do đó $x+3 \geq 1 \Rightarrow(x+3)^{2} \geq 1 \Rightarrow P \geq-5$.

Dấu bằng xảy ra khi $a=b=-1$.

Vậy giá trị nhỏ nhất của $P$ là $-5$.