🔺Đề thi thử số 5 - bộ Kết nối tri thức (phần tự luận) SVIP

Hướng dẫn giải:

Tổng số khách là $50+x$.

Tổng số tiền mà mỗi khách phải trả là $300-5 x$ (đơn vị tính là nghìn đồng).

Tổng tiền thu là $(50+x)(300-5 x)=-5 x^2+50 x+15000$.

Để công ty không bị lỗ thì phải có $-5 x^2+50 x+15000 \geq 15080 \Leftrightarrow x^2-10 x+16 \leq 0 \Leftrightarrow 2 \leq x \leq 8$.

Vậy số nguyên lớn nhất để chuyến đi không bị lỗ là $x=8$.

Hướng dẫn giải:

Phương trình $\sqrt{-x^2-4 x+m}=x-1 \Leftrightarrow\left\{\begin{aligned}x \geq 1 \\ -x^2-4 x+m=x^2-2 x+1\end{aligned} \Leftrightarrow\left\{\begin{aligned}x \geq 1 \\ m=2 x^2+2 x+1 \, \, \, \left(^*\right)\end{aligned}\right.\right.$

Phương trình có nghiệm $\Leftrightarrow(*)$ có nghiệm lớn hơn hoặc bằng $1$.

Xét hàm số $f(x)=2 x^2+2 x+1$ với $x \geq 1$.

Ta có bảng biến thiên:

Từ bảng biến thiên suy ra điều kiện của $m$ là $m \geq 5$.

Hướng dẫn giải:

Vì $A$ thuộc $d$ nên $A\left(a ; \dfrac{5-2 a}{3}\right)$.

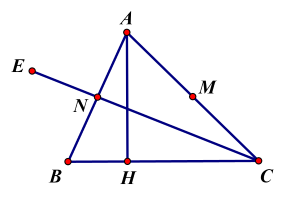
$M$ là trung điểm của $A C$ nên $\left\{\begin{aligned}x_C=2 x_M-x_A \\ y_C=2 y_M-y_A\end{aligned} \Rightarrow C\left(4-a, \dfrac{1+2 a}{3}\right)\right.$.

Ta có $\overrightarrow{A H}=\left(-a ; \dfrac{-14+2 a}{3}\right)$, $\overrightarrow{C H}=\left(a-4 ; \dfrac{10-2 a}{3}\right)$.

Vì $A H$ vuông góc với $C H$ nên $\overrightarrow{A H} . \overrightarrow{C H}=0 \Leftrightarrow-a(a-4)+\left(\dfrac{-14+2 a}{3}\right)\left(\dfrac{10-2 a}{3}\right)=0 \Leftrightarrow\left[\begin{aligned}a=-2 \\ a=\dfrac{70}{13}\end{aligned}\right.$.

Với $a=\dfrac{70}{13} \Rightarrow x_C=4-\dfrac{70}{13}=\dfrac{-18}{13}<0$ (loại).

Với $a=-2$ suy ra $A(-2 ; 3),$ $C(6 ;-1)$ (thỏa mãn).

Đường thẳng $B C$ đi qua $H$ và $C$ nên có phương trình $x-3 y-9=0$.

Đường thẳng $C E$ đi qua $C$ và $E$ nên có phương trình $x+17 y+11=0$.

$B$ thuộc $B C$ nên $B(3 b+9 ; b)$.

Gọi $N$ là trung điểm của $A B$ ta có $N\left(\dfrac{3 b+7}{2} ; \dfrac{b+3}{2}\right)$.

$N$ thuộc $C E$ nên $\dfrac{3 b+7}{2}+17\left(\dfrac{b+3}{2}\right)+11=0 \Leftrightarrow b=-4$.

Vậy $B(-3 ;-4)$.

Hướng dẫn giải:

Gọi $G$ là điểm thỏa mãn $ \overrightarrow{G A}+ \overrightarrow{G B}+ \overrightarrow{G C}=0$.

Tọa độ điểm $G(2 ; 3)$.

Gọi $N$ là điểm thỏa mãn $ \overrightarrow{N A}+2  \overrightarrow{NB}=0$

Tọa độ điểm $N(1 ; 5)$.

Từ đó ta thấy $G, \, N$ nằm về hai phía so với đường thẳng $\Delta$.

Ta có: $| \overrightarrow{M A}+ \overrightarrow{M B}+ \overrightarrow{M C}|=|3 \overrightarrow{ M G}|=3 M G$ và $| \overrightarrow{M A}+2  \overrightarrow{M B}|=|3  \overrightarrow{M N}|=3 M N$.

Khi đó: $| \overrightarrow{M A}+ \overrightarrow{M B}+ \overrightarrow{M C}|+| \overrightarrow{M A}+2  \overrightarrow{M B}|=3(M G+M N) \geq 3 G N$.

Do đó $| \overrightarrow{M A}+ \overrightarrow{M B}+ \overrightarrow{M C}|+| \overrightarrow{M A}+2  \overrightarrow{M B}|$ nhỏ nhất là bằng $3 G N$, đạt được khi ba điểm $G, \,M, \, N$ thẳng hàng.

Suy ra là giao điểm của đường thẳng $G N$ và $\Delta$.

Ta có $ \overrightarrow{G N}=(-1 ; 2)$, phương trình đường thẳng $G N$ là $ 2(x-1)+(y-5)=0 \Leftrightarrow 2 x+y-7=0 .$

Tọa độ điểm $M$ là nghiệm của hệ phương trình:

$\left\{\begin{aligned}2 x+y-7=0 \\ 3 x-y+1=0\end{aligned} \Leftrightarrow\left\{\begin{aligned}x=\dfrac{6}{5} \\ y=\dfrac{23}{5}\end{aligned}\right.\right.$.