Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 5 (thời gian: 90 phút) SVIP
(2,5 điểm)
1) Giải các phương trình sau:
a) \(3x^2-6x=0\);
b) \(x^2-4=0\);
c) \(x^2+6x-7=0\).
2) Giải hệ phương trình:
a) \(\left\{{}\begin{matrix}x-y=1\\x+y=3.\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x-5y=-7\\2x+7y=3.\end{matrix}\right.\)
Hướng dẫn giải:
1) a) \(3x^2-6x=0\Leftrightarrow3x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2.\end{matrix}\right.\)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{0;2\right\}\).
b) \(x^2-4=0\Leftrightarrow\left(x-2\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2.\end{matrix}\right.\)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{-2;2\right\}\).
c) \(x^2+6x-7=0\Leftrightarrow x^2+7x-x-7=0\)
\(\Leftrightarrow x\left(x+7\right)-\left(x+7\right)=0\Leftrightarrow\left(x+7\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+7=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-7\\x=1.\end{matrix}\right.\)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{-7;1\right\}\).
2) a) \(\left\{{}\begin{matrix}x-y=1\\x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=4\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1.\end{matrix}\right.\)
Vậy nghiệm của hệ phương trình đã cho là \(\left(x;y\right)=\left(2;1\right)\).
b) \(\left\{{}\begin{matrix}x-5y=-7\\2x+7y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-10y=-14\\2x+7y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-17y=-17\\x=-7+5y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=-7+5y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=1.\end{matrix}\right.\)
Vậy nghiệm của hệ phương trình đã cho là \(\left(x;y\right)=\left(-2;1\right)\).
(2,0 điểm) Cho phương trình \(x^2-2\left(m+1\right)x+m^2+4=0\) (1), (\(m\) là tham số).
a) Giải phương trình với \(m=2\).
b) Tìm \(m\) để phương trình (1) có $2$ nghiệm.
Hướng dẫn giải:
a) Thay $m=2$ vào phương trình (1) ta được:
\(x^2-6x+8=0\Leftrightarrow\left(x-2\right)\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)
Vậy với \(m=2\) tập nghiệm của phương trình đã cho là \(S=\left\{2;4\right\}\).
b) Phương trình (1) có $2$ nghiệm khi và chỉ khi \(\Delta'\ge0\).
\(\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2+4\right)=2m-3\)
\(\Delta'\ge0\Rightarrow2m-3\ge0\Leftrightarrow m\ge\dfrac{3}{2}\).
Vậy với \(m\ge\dfrac{3}{2}\) thì thỏa mãn ycbt.
(1,5 điểm) Giải bài toán sau bằng cách lập hệ phương trình
Hai vòi nước cùng chảy vào một bể cạn thì sau \(\dfrac{24}{5}\) giờ đầy bể. Mỗi giờ lượng nước vòi I chảy bằng \(\dfrac{3}{2}\) lượng nước chảy được của vòi II. Hỏi nếu mỗi vòi chảy riêng thì sau bao lâu đầy bể?
Hướng dẫn giải:
Gọi thời gian vòi I, vòi II chảy một mình đầy bể lần lượt là $x$, $y$ (giờ) ($x,y>0$).
Trong $1$ giờ, vòi I, vòi II chảy được lần lượt số phần bể là: \(\dfrac{1}{x},\dfrac{1}{y}\) (bể).
Vì hai vòi nước cùng chảy vào một bể cạn thì sau \(\dfrac{24}{5}\) giờ đầy bể nên ta có phương trình
\(\dfrac{24}{5}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{24}\). (1)
Vì mỗi giờ lượng nước vòi I chảy bằng \(\dfrac{3}{2}\) lượng nước chảy được của vòi II nên ta có phương trình
\(\dfrac{1}{x}=\dfrac{3}{2}.\dfrac{1}{y}\Leftrightarrow\dfrac{2}{x}-\dfrac{3}{y}=0\). (2)
Từ (1) và (2) ta có hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{24}\\\dfrac{2}{x}-\dfrac{3}{y}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{8}\\\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=12\end{matrix}\right.\) (thỏa mãn)
Vậy thời gian để vòi I, vòi II chảy một mình đầy bể lần lượt là $8$ giờ, $12$ giờ.
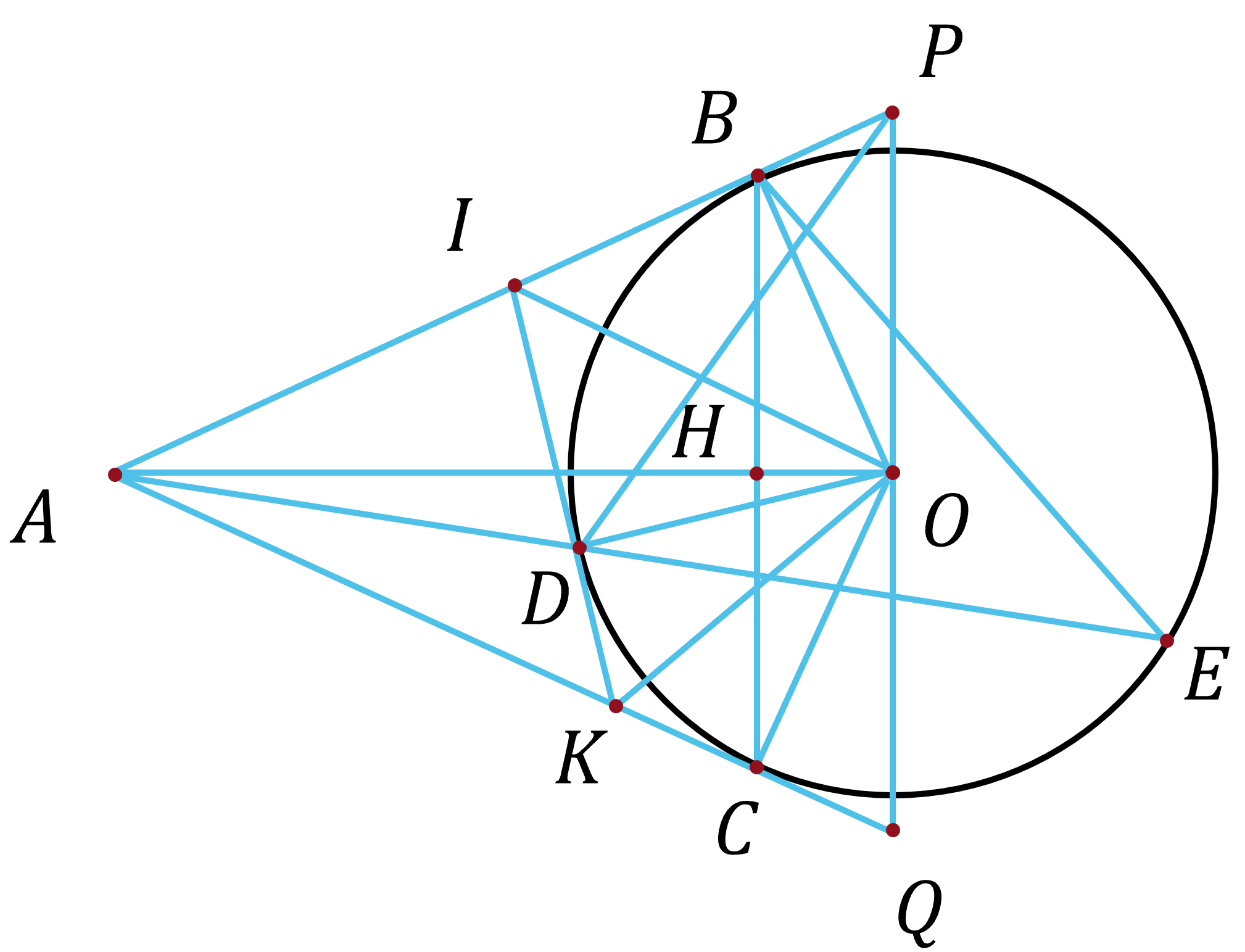
(4,0 điểm) Cho điểm $A$ nằm ngoài đường tròn $(O)$. Từ $A$ kẻ hai tiếp tuyến $AB$, $AC$ và cát tuyến $ADE$ tới đường tròn đó ($B$, $C$ là tiếp điểm; $D$ nằm giữa $A$ và $E$). Gọi $H$ là giao điểm của $AO$ và $BC$.
a) Chứng minh tứ giác $ABOC$ nội tiếp.
b) Chứng minh $AH.AO= AD.AE$.
c) Tiếp tuyến tại $D$ của đường tròn $(O)$ cắt $AB$, $AC$ theo thứ tự tại $I$ và $K$. Qua điểm $O$ kẻ đường thẳng vuông góc với $OA$ cắt $AB$ tại $P$ và cắt $AC$ tại $Q$. Chứng minh $IP+KQ \ge PQ$.
Hướng dẫn giải:
a) Chứng minh tứ giác $ABOC$ nội tiếp.
Ta có $\widehat{ABO} = \widehat{ACO} =90^\circ$ do đó $B$, $C$ cùng nhìn $AO$ dưới góc $90^\circ$ nên $B$, $C$ cùng thuộc đường tròn đường kính $AO$.
Vậy tứ giác $ABOC$ nội tiếp.
b) Chứng minh $AH.AO= AD.AE$.
Tam giác $ABC$ có $AO$ là tia phân giác nên đồng thời cũng là đường cao suy ra $AO \bot BC$ tại $H$.
Xét tam giác $ABO$ vuông tại $B$ đường cao $BH$:
$AH.AO=AB^2$ (hệ thức trong tam giác vuông)
Có $\triangle ABD \backsim \triangle AEB$ (g.g)
suy ra \(\dfrac{AB}{AE}=\dfrac{AD}{AB}\Leftrightarrow AD.AE=AB^2\).
Suy ra $AH.AO=AD.AE$.
c) Chứng minh $IP+KQ \ge PQ$.
Tam giác $APQ$ cân tại $A$ nên $\widehat{APQ} = \widehat{AQP}$.
Theo tính chất hai tiếp tuyến cắt nhau, ta có: $\widehat{OIB} = \widehat{OID}$, $\widehat{OKD} =\widehat{OKC}$.
Xét tứ giác $PQKI$ có:
$\widehat{IPQ} +\widehat{PQK} +\widehat{QKI}+\widehat{KIP} =360^\circ$
$\Leftrightarrow 2\widehat{IPQ} +2\widehat{OIB} +2\widehat{OKC} =360^\circ$
$\Leftrightarrow \widehat{IPQ} +\widehat{OIB} +\widehat{OKC} =180^\circ$
mà $\widehat{IPQ} +\widehat{OIB} +\widehat{IOP} =180^\circ$
suy ra $\widehat{OKC} =\widehat{IOP}$.
Từ đó suy ra $\triangle IOP \backsim \triangle OKQ$ (g.g)
suy ra \(\dfrac{IP}{OQ}=\dfrac{OP}{KQ}\Leftrightarrow IP.KQ=OP.OQ=\dfrac{PQ^2}{4}\).
Lại có \(\left(IP+KQ\right)^2\ge4.IP.KQ=PQ^2\Rightarrow IP+KQ\ge PQ\).
