Đề số 3 (thời gian: 90 phút) SVIP

Hướng dẫn giải:

1. Thế $x=25$ vào biểu thức $A$ ta được:

\(A=\dfrac{\sqrt{25}+1}{25-4}=\dfrac{5+1}{21}=\dfrac{2}{7}\).

2. \(B=\dfrac{18-\sqrt{x}}{x-4}+\dfrac{4}{2-\sqrt{x}}+\dfrac{\sqrt{x}+3}{\sqrt{x}+2}\) (\(x\ge0,x\ne4\))

\(=\dfrac{18-\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{4\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{18-\sqrt{x}-4\sqrt{x}-8+x+\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\).

3. \(P=A.B=\dfrac{\sqrt{x}+1}{x-4}.\dfrac{\sqrt{x}-2}{\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)\

\(=\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}=\dfrac{1}{\sqrt{x}+2}-\dfrac{1}{\left(\sqrt{x}+2\right)^2}\)

\(=-\left[\left(\dfrac{1}{\sqrt{x}+2}\right)^2-2.\dfrac{1}{\sqrt{x}+2}.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]+\dfrac{1}{4}\)

\(=-\left(\dfrac{1}{\sqrt{x}+2}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)

Dấu "\(=\)" xảy ra khi \(\dfrac{1}{\sqrt{x}+2}-\dfrac{1}{2}=0\Leftrightarrow x=0\) (thỏa mãn).

Vậy giá trị lớn nhất của \(P\) là \(\dfrac{1}{4}\) đạt tại \(x=0\).

Hướng dẫn giải:

Gọi số sản phẩm tháng đầu mỗi tổ sản xuất được lần lượt là $x$, $y$ (sản phẩm) ($x,y>0$).

Vì trong tháng đầu, hai tổ làm được $600$ sản phẩm nên ta có phương trình:

$x+y=600$ (1)

Vì sang tháng thứ hai, tổ I vượt mức $10\%$ và tổ hai vượt mức $20\%$ so với tháng đầu, do đó tháng thứ hai cả hai tổ làm được $685$ sản phẩm nên ta có phương trình

$x+10\%x+y+20\%y=685 \Leftrightarrow 1,1x+1,2y=685$ (2) 

Từ (1) và (2) ta có hệ phương trình: 

\(\left\{{}\begin{matrix}x+y=600\\1,1x+1,2y=685\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1,1x+1,1y=660\\1,1x+1,2y=685\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0,1y=25\\x+y=600\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=250\\x=350.\end{matrix}\right.\) (thỏa mãn)

Vậy tháng đầu tổ I sản xuất được $350$ sản phẩm, tổ II sản xuất được $250$ sản phẩm.

Hướng dẫn giải:

1. Phương trình hoành độ giao điểm của $(P)$ và $(d)$ là 

$x^2=x+2 \Leftrightarrow x^2-x-2=0 \Leftrightarrow (x+1)(x-2)=0 $\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2.\end{matrix}\right.\)

Với \(x=-1\) suy ra \(y=1\) ta có điểm \(\left(-1;1\right)\).

Với \(x=2\) suy ra \(y=4\) ta có điểm \(\left(2;4\right)\). 

Vậy $(P)$ và $(d)$ cắt nhau tại hai điểm $(-1;1)$ và $(2;4)$. 

2. Với \(m=0\) hệ phương trình đã cho tương đương với:

\(\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\) thỏa mãn. 

Với $m \neq 0$ hệ phương trình đã cho tương đương với: 

\(\left\{{}\begin{matrix}m^2x+my=2m^2\\x+my=m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m^2-1\right)x=2m^2-m-1\\y=2m-mx\end{matrix}\right.\) (I) 

Với \(m=1\) hệ (I) tương đương với: 

\(\left\{{}\begin{matrix}0x=0\\y=2-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\inℝ\\y=2-x\end{matrix}\right.\) (loại)

Với \(m=-1\) hệ (I) tương đương với:

\(\left\{{}\begin{matrix}0x=2\\y=-2+x\end{matrix}\right.\) (vô nghiệm) 

Với \(m\ne\pm1\) hệ (I) tương đương với:

\(\left\{{}\begin{matrix}x=\dfrac{\left(2m+1\right)\left(m-1\right)}{\left(m-1\right)\left(m+1\right)}\\y=2m-mx\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m+1}\\y=2m-m\dfrac{2m+1}{m+1}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m+1}\\y=\dfrac{m-2m^2}{m+1}\end{matrix}\right.\).

Ta có: \(x=\dfrac{2m+1}{m+1}=\dfrac{2m+2-1}{m+1}=2-\dfrac{1}{m+1}\).

Để \(x\) nhận giá trị nguyên thì \(\dfrac{1}{m+1}\) nhận giá trị nguyên. 

\(\dfrac{1}{m+1}=k\) (\(k\) nguyên)

\(\Leftrightarrow m+1=\dfrac{1}{k}\Leftrightarrow m=\dfrac{1}{k}-1=\dfrac{1-k}{k}\).

\(y=\dfrac{m-2m^2}{m+1}=\dfrac{\dfrac{1-k}{k}-2\left(\dfrac{1-k}{k}\right)^2}{\dfrac{1-k}{k}+1}=\dfrac{-3k^2+5k+2}{k}=-3k+5+\dfrac{2}{k}\)

\(y\) nguyên, \(k\) nguyên suy ra \(\dfrac{2}{k}\)nguyên do đó \(k\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\)

Suy ra \(m\in\left\{-\dfrac{3}{2};-2;0;-\dfrac{1}{2}\right\}\).

Vậy \(m\in\left\{-\dfrac{3}{2};-2;0;-\dfrac{1}{2}\right\}\) thỏa mãn yêu cầu bài toán. 

Hướng dẫn giải:

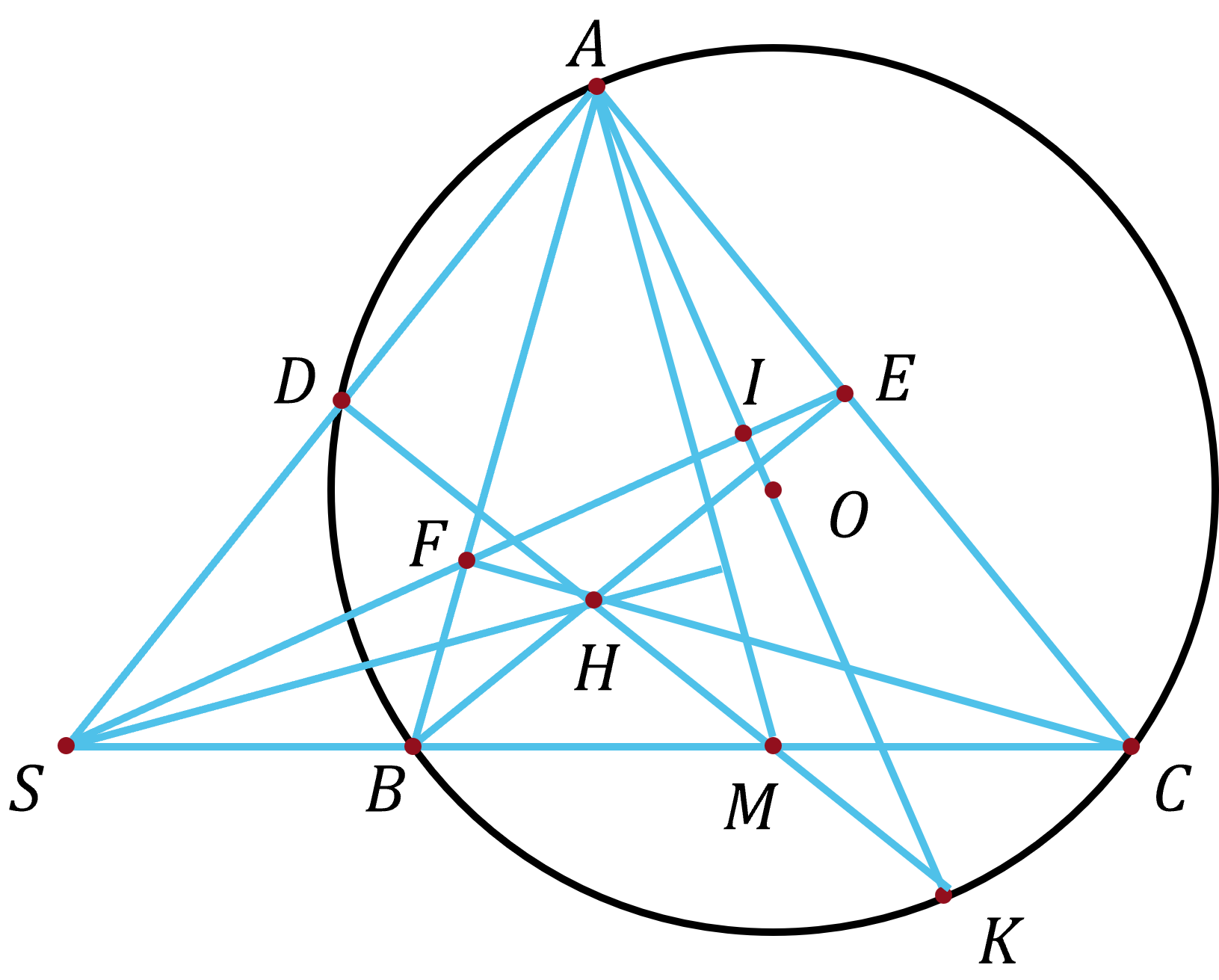
1. Chứng minh tứ giác $BCEF$ nội tiếp. 

Có $\widehat{BFC} = \widehat{BEC} = 90^\circ$ do đó $F$, $E$ cùng nhìn $BC$ dưới một góc $90^\circ$ nên $F$, $E$ cùng thuộc đường tròn đường kính $BC$. 

Suy ra tứ giác $BCEF$ nội tiếp. 

2. Chứng minh $OA \bot EF$. 

Gọi $I$ là giao điểm của $OA$ và $EF$. 

Vì tứ giác $BCEF$ nội tiếp nên $\widehat{FBC} = \widehat{FEA}$.

Suy ra $\widehat{AIE} = 180^\circ - \widehat{IAE} - \widehat{IEA} = 180^\circ - \widehat{IAE} - \widehat{FBC} = 180^\circ$\(-\dfrac{1}{2}sđ\stackrel\frown{CK}-\dfrac{1}{2}sđ\stackrel\frown{AC}\)

$=180^\circ$\(-\dfrac{1}{2}sđ\stackrel\frown{AK}\)$=180^\circ - 90^\circ = 90^\circ$. 

Do đó $OA \ bot EF$.

3.

- Chứng minh $H$, $M$, $K$ thẳng hàng. 

Có $\widehat{KBA} = 90^\circ$ suy ra $KB \bot BA$ mà $CF \bot BA$ suy ra $KB \parallel CF$. 

Tương tự, có $\widehat{KCA} = 90^\circ$ suy ra $KC \bot CA$ mà $BE \bot CA$ suy ra $KC \parallel BE$. 

Xét tứ giác $BHCK$ có: $BH \parallel KC$, $KB \parallel CK$ suy ra tứ giác $BHCK$ là hình bình hành. 

Do đó hai đường chéo $BC$, $HK$ cắt nhau tại trung điểm mỗi đường. 

Mà $M$ là trung điểm của $BC$ suy ra $M$ là trung điểm của $HK$. 

Do đó $H$, $M$, $K$ thẳng hàng. 

- Chứng minh $SH \bot AM$.

Gọi $D$ là giao điểm của $SA$ và $(O)$. 

Có $\triangle SBF \backsim \triangle SCE$ (g.g) 

suy ra \(\dfrac{SF}{SC}=\dfrac{SB}{SE}\Rightarrow SF.SE=SB.SC\).

Có $\triangle SBD \backsim \triangle SAC$ (g.g) 

suy ra \(\dfrac{SB}{SA}=\dfrac{SD}{SC}\Rightarrow SB.SC=SA.SD\).

Suy ra \(SF.SE=SA.SD\Rightarrow\dfrac{SF}{SA}=\dfrac{SD}{SE}\).

Xét $\triangle SFD$ và $\triangle SAE$ có: 

\(\dfrac{SF}{SA}=\dfrac{SD}{SE}\)

$widehat{FSD} = \widehat{ASE}$ (góc chung)

suy ra $\triangle SFD \backsim \triangle SAE$ (c.g.c)

\(\Rightarrow\widehat{SDF}=\widehat{SEA}\)

do đó tứ giác $ADFE$ nội tiếp.

Mà tứ giác $AFHE$ nội tiếp đường tròn đường kính $AH$ (vì $F$, $E$ cùng nhìn $AH$ dưới một góc vuông$ 

do đó $ADFHE$ nội tiếp đường tròn đường kính $AH$.

Suy ra $\widehat{ADH} = 90^\circ$. 
Mà $\widehat{ADK} = 90^\circ$ suy ra $D$, $H$, $K$ thẳng hàng và $KH \bot AS$. Lại có $H$, $M$, $K$ thẳng hàng nên $MH \bot AS$.

Xét tam giác $ASM$ có: $AH \bot SM$, $MH \bot AS$ suy ra $H$ là trực tâm của tam giác $ASM$. 

Suy ra $SH \bot AM$.

Hướng dẫn giải:

- Tìm GTLN

\(S^2=\left(\sqrt{4-x^2}+\sqrt{4-y^2}+\sqrt{4-z^2}\right)^2\)

\(\le\left(1^2+1^2+1^2\right)\left(12-x^2-y^2-z^2\right)=18\)

Suy ra \(S\le3\sqrt{2}\).

Dấu "\(=\)" xảy ra khi \(x=y=z=\sqrt{2}\).

- Tìm GTNN

Đặt \(\sqrt{4-x^2}=a,\sqrt{4-y^2}=b,\sqrt{4-z^2}=c\).

Suy ra \(0\le a,b,c\le\sqrt{3},a^2+b^2+c^2=6\).

Ta có: 

\(\left(\sqrt{3}-a\right)\left(\sqrt{3}-b\right)\left(\sqrt{3}-c\right)\ge0\)

\(\Leftrightarrow3\sqrt{3}-3\left(a+b+c\right)+\sqrt{3}\left(ab+bc+ca\right)\ge abc\ge0\)

\(\Leftrightarrow3\sqrt{3}-3S+\sqrt{3}.\dfrac{S^2-6}{2}\ge0\)

\(\Leftrightarrow-3S+\dfrac{\sqrt{3}S^2}{2}\ge0\)

\(\Leftrightarrow S\left(S-2\sqrt{3}\right)\ge0\Leftrightarrow S\ge2\sqrt{3}\)

Dấu "$=$" xảy ra chẳng hạn \(a=b=\sqrt{3},c=0\Leftrightarrow x=y=1,z=2\).