Đề số 4 (thời gian: 90 phút) SVIP

Hướng dẫn giải:

1. Thay $x=9$ vào $A$: \(A=\dfrac{\sqrt{9}-1}{\sqrt{9}+1}=\dfrac{1}{2}\).

Vậy $x=9$ thì giá trị của \(A\) bằng \(\dfrac{1}{2}\).

2.  \(B=\dfrac{\sqrt{x}+5}{\sqrt{x}+1}-\dfrac{1}{1-\sqrt{x}}+\dfrac{8}{x-1}\) (\(x\ge0,x\ne1\))

\(\begin{aligned} & =\frac{\sqrt{x}+5}{\sqrt{x}+1}+\frac{1}{\sqrt{x}+1}+\frac{8}{(\sqrt{x}-1)(\sqrt{x}+1)} \\ & =\frac{(\sqrt{x}+5)(\sqrt{x}-1)+\sqrt{x}+1+8}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{x+4 \sqrt{x}-5+\sqrt{x}+1+8}{(\sqrt{x}-1)(\sqrt{x}+1)} \\ & =\frac{x+5 \sqrt{x}+4}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{(\sqrt{x}+1)(\sqrt{x}+4)}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{\sqrt{x}+4}{\sqrt{x}-1} \end{aligned}\)

3. Điều kiện: \(x \ge 0, x \neq 1\).

\(\displaystyle P=A \cdot B=\frac{\sqrt{x}-1}{\sqrt{x}+1} \cdot \frac{\sqrt{x}+4}{\sqrt{x}-1}=\frac{\sqrt{x}+4}{\sqrt{x}+1}=1+\frac{3}{\sqrt{x}+1}\)

Ta có: \(\sqrt{x}+1\ge1\Leftrightarrow\dfrac{3}{\sqrt{x}+1}\le3\) do đó \(P\le4\).

\(\sqrt{x}+1\ge1\Rightarrow\dfrac{3}{\sqrt{x}+1}>0\) do đó \(P>1\).

Mà \(P\) nguyên nên \(P\in\left\{2;3;4\right\}\).

TH1: \(P=2\)

\(\displaystyle P=2 \Rightarrow 1+\frac{3}{\sqrt{x}+1}=2 \Leftrightarrow \frac{3}{\sqrt{x}+1}=1 \Leftrightarrow \sqrt{x}+1=3 \Leftrightarrow \sqrt{x}=2 \Leftrightarrow x=4\) (tm)

TH2: $P=3$

\(\displaystyle P=3 \Rightarrow 1+\frac{3}{\sqrt{x}+1}=3 \Leftrightarrow \frac{3}{\sqrt{x}+1}=2 \Leftrightarrow \sqrt{x}+1=\frac{3}{2} \Leftrightarrow \sqrt{x}=\frac{1}{2} \Leftrightarrow x=\frac{1}{4}\) (tm)

TH3: $P=4$

\(\displaystyle P=4 \Rightarrow 1+\frac{3}{\sqrt{x}+1}=4 \Leftrightarrow \frac{3}{\sqrt{x}+1}=3 \Leftrightarrow \sqrt{x}+1=1 \Leftrightarrow \sqrt{x}=0 \Leftrightarrow x=0\) (tm)

Vậy \(x\in\left\{0;\dfrac{1}{4};4\right\}\) thỏa mãn ybct.

Hướng dẫn giải:

1. \(\left\{\begin{array} { l } { 3 x - 2 y = 5 } \\ { x + 2 y = 4 } \end{array} \Leftrightarrow \left\{\begin{array} { c } { 6 x - 2 y = 1 0 } \\ { x + 2 y = 4 } \end{array} \Leftrightarrow \left\{\begin{array} { c } { 7 x = 1 4 } \\ { x + 2 y = 4 } \end{array} \Leftrightarrow \left\{\begin{array} { c } { x = 2 } \\ { 2 + 2 y = 4 } \end{array} \Leftrightarrow \left\{\begin{array}{l} x=2 \\ y=1 \end{array}\right.\right.\right.\right.\right.\)

Vậy hệ phương trình có nghiệm \(\left(x;y\right)=\left(2;1\right)\).

2. Điều kiện: $x \ge -1, y \ge 2$.

\(\begin{aligned} & \left\{\begin{array} { l } { 2 \sqrt { x + 1 } - 3 \sqrt { y - 2 } = 5 } \\ { 4 \sqrt { x + 1 } + \sqrt { y - 2 } = 1 7 } \end{array} \Leftrightarrow \left\{\begin{array} { c } { 2 \sqrt { x + 1 } - 3 \sqrt { y - 2 } = 5 } \\ { 1 2 \sqrt { x + 1 } + 3 \sqrt { y - 2 } = 5 1 } \end{array} \Leftrightarrow \left\{\begin{array}{c} 2 \sqrt{x+1}-3 \sqrt{y-2}=5 \\ 14 \sqrt{x+1}=56 \end{array}\right.\right.\right. \\ & \Leftrightarrow\left\{\begin{array} { c } { 2 \sqrt { x + 1 } - 3 \sqrt { y - 2 } = 5 } \\ { \sqrt { x + 1 } = 4 } \end{array} \Leftrightarrow \left\{\begin{array}{c} 2.4-3 \sqrt{y-2}=5 \\ \sqrt{x+1}=4 \end{array}\right.\right. \\ & \Leftrightarrow\left\{\begin{array} { l } { \sqrt { y - 2 } = 1 } \\ { \sqrt { x + 1 } = 4 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { y - 2 = 1 } \\ { x + 1 = 1 6 } \end{array} \Leftrightarrow \left\{\begin{array}{ll} y=3 & \text{(tm)} \\ x=15 & \text{(tm)} \end{array}\right.\right.\right. \\ & \end{aligned}\)Vậy hệ phương trình đã cho có nghiệm là \(\left(x;y\right)=\left(15;3\right)\).

Hướng dẫn giải:

Gọi thời gian vòi một và vòi hai chảy một mình đầy bể lần lượt là $x$, $y$ (giờ) ($x,y>0$).

Mỗi giờ hai vòi chảy được lần lượt $\displaystyle \frac{1}{x}, \frac{1}{y}$ (bể).

Do hai vòi nước cùng chảy vào bể không có nước thì sau $12$ giờ đầy bể nên ta có phương trình

\(\dfrac{12}{x}+\dfrac{12}{y}=1\). (1)

Vì nếu người ta mở cả hai vòi chảy trong $4$ giờ rồi khóa vòi hai lại và để vòi một chảy tiếp $14$ giờ nữa thì mới đầy bể nên ta có phương trình

\(4\left(\dfrac{1}{x}+\dfrac{1}{y}\right)+\dfrac{14}{x}=1\Leftrightarrow\dfrac{18}{x}+\dfrac{4}{y}=1\). (2)

Từ (1) và (2) ta có hệ phương trình: 

\(\left\{{}\begin{matrix}\dfrac{12}{x}+\dfrac{12}{y}=1\\\dfrac{18}{x}+\dfrac{4}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{21}\\\dfrac{1}{y}=\dfrac{1}{28}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=21\\y=28\end{matrix}\right.\) (tm)

Vậy thời gian vòi một, vòi hai chảy một mình đầy bể lần lượt là $21$ giờ, $28$ giờ. 

Hướng dẫn giải:

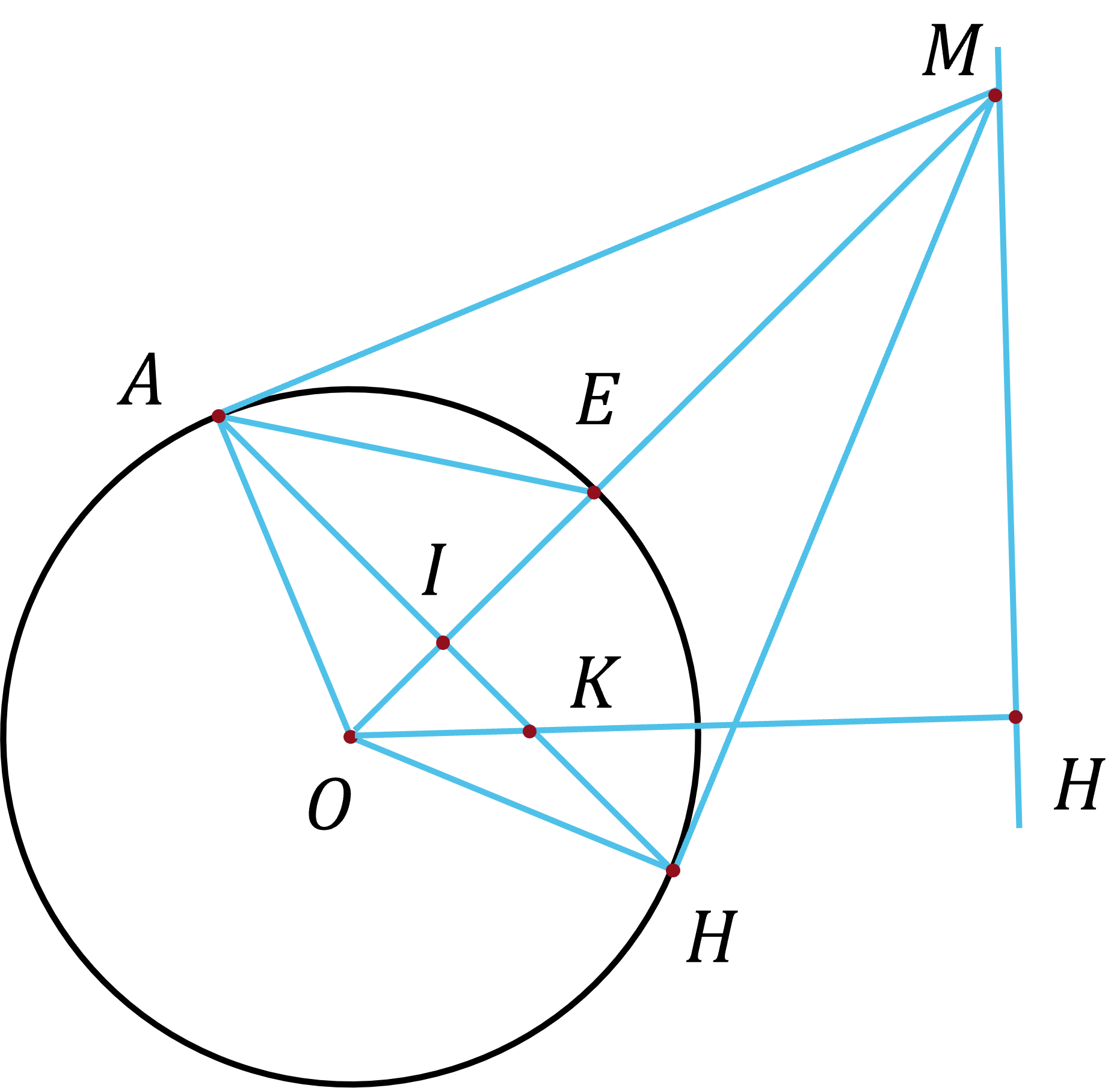
a) Chứng minh $AOBM$ là tứ giác nội tiếp.

Ta có $\widehat{MAO} =\widehat{MBO}=90^\circ$ 

suy ra $A$, $B$ cùng nhìn $MO$ dưới một góc $90^\circ$ nên $A$, $B$ cùng thuộc đường tròn đường kính $MO$. 

Vậy tứ giác $AOBM$ nội tiếp. 

b) Chứng minh $OI.OM=OK.OH$.

Ta có $\triangle OIK \backsim \triangle OHM$ (g.g) 

suy ra \(\dfrac{OI}{OH}=\dfrac{OK}{OM}\Leftrightarrow OI.OM=OK.OH\).

c) Chứng minh $E$ là tâm đường tròn nội tiếp tam giác $MAB$.

Xét $(O)$ có: $\widehat{AOE} = \widehat{BOE}$ (tính chất hai tiếp tuyến cắt nhau)

suy ra \(sđ\stackrel\frown{AE}=sđ\stackrel\frown{BE}\) nên $\widehat{BAE} = \widehat{MAE}$.

Xét tam giác $MAB$ có: 

$MO$ là tia phân giác của $\widehat{AMB}$,

$AE$ là tia phân giác của $\widehat{BAM}$ 

hai tia phân giác này cắt nhau tại $E$ suy ra $E$ là tâm đường tròn nội tiếp tam giác $MAB$.

d) Tìm vị trí của $M$ trên đường thẳng $d$ để diện tích tam giác $OIK$ có giá trị lớn nhất.

Có \(OH.OK=OI.OM=OB^2=R^2\) suy ra \(OK=\dfrac{R^2}{OH}\).

Mà \(OH\) không đổi, $R$ không đổi nên $OK$ không đổi. 

\(S_{OIK}=\dfrac{1}{2}OI.IK\le\dfrac{1}{4}\left(OI^2+IK^2\right)=\dfrac{1}{4}OK^2\)

Dấu "\(=\)" xảy ra khi \(OI=IK\) khi đó \(1=\dfrac{OI}{IK}=\dfrac{OH}{HM}\) suy ra \(OH=HM\).

Vậy điểm $M$ nằm trên đường thẳng $(d)$ sao cho $OH=HM$ thì diện tích tam giác $OIK$ đạt giá trị lớn nhất. 

Hướng dẫn giải:

Ta có \(x+y\ge2\sqrt{xy}\Rightarrow0< xy\le\dfrac{1}{4}\).

\(\displaystyle \begin{aligned} & A=\left(x+\frac{1}{x}\right)^2+\left(y+\frac{1}{y}\right)^2=x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}+4 \\ & \geq 2 x y+2 \frac{1}{x y}+4=2\left(x y+\frac{1}{16 x y}+\frac{15}{16 x y}\right)+4 \\ & \Rightarrow A \geq 2\left(2 \sqrt{x y \cdot \frac{1}{16 x y}}+\frac{15}{16 x y}\right)+4=2\left(2 \cdot \frac{1}{4}+\frac{15}{16 \cdot \frac{1}{4}}\right)+4=\frac{25}{2} \end{aligned}\)

Dấu "$=$" xảy ra khi \(x=y=\dfrac{1}{2}\).

Vậy giá trị nhỏ nhất của \(A\) là \(\dfrac{25}{2}\) đạt tại \(x=y=\dfrac{1}{2}\).