Bài học cùng chủ đề
- Hình bình hành
- Hình thoi
- Khái niệm và tính chất hình bình hành
- Dấu hiệu nhận biết hình bình hành (theo cạnh)
- Dấu hiệu nhận biết hình bình hành (theo góc và đường chéo)
- Hình thoi
- Khái niệm và tính chất của hình bình hành
- Dấu hiệu nhận biết hình bình hành
- Bài tập tự luận: Hình bình hành
- Hình thoi
- Bài tập tự luận: Hình thoi
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Dấu hiệu nhận biết theo góc và đường chéo. Tứ giác có:
+ các góc đối bằng nhau là một hình bình hành.
+ hai đường chéo cắt nhau tại trung điểm mỗi đường là một hình bình hành.
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
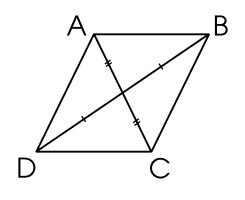
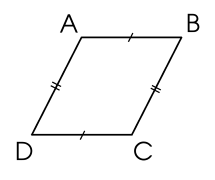
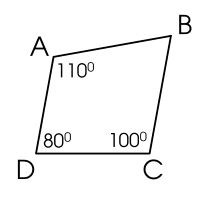
Những tứ giác nào dưới đây là hình bình hành?



Câu 2 (1đ):
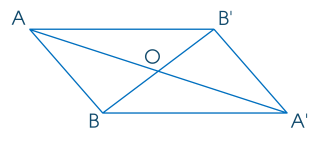
Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A', B' là các điểm sao cho O là trung điểm của AA', BB'.
Khi đó, tứ giác AB'A'B có hai đường chéo AA' và BB' cắt nhau tại trung điểm mỗi đường, suy ra AB'A'B là
hình thang.
hình bình hành.
hình thang cân.
Câu 3 (1đ):
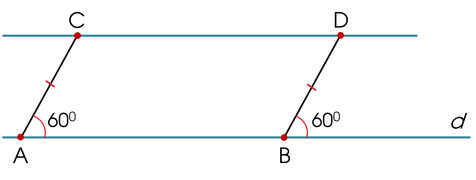
Cho hình vẽ, có CD // AB nên ABDC là hình thang.
AC=BD (1)
Và A=B=60∘, hai góc ở vị trí đồng vị
Suy ra (2)
Từ (1) và (2) ta suy ra tứ giác ABDC là .
AC // BD hình bình hành AB // CD hình thang hình thang cân
(Kéo thả hoặc click vào để điền)
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- [âm nhạc]
- tiếp theo là các dấu hiệu liên quan tới
- góc và đường chéo thì các bạn sẽ ghi lại
- cho thầy định lý 3 tứ giác mà có các góc
- đối bằng nhau cũng là một hình bình hành
- và tứ giác có hai đường chéo cắt nhau
- tại trung điểm của mỗi đường là hình
- bình hành vậy ta sẽ có hai dấu hiệu tiếp
- theo để nhận biết một tứ giác là hình
- bình hành thứ nhất là các góc đối bằng
- nhau thứ hai là hai đường chéo cắt nhau
- tại trung điểm của mỗi đường
- thấy có thể viết ngắn gọn dưới dạng giả
- thiết kết luận như sau nếu Cho tứ giác
- ABCD mà có các góc đối là góc A bằng góc
- C và góc B bằng góc D thì tứ giác đó là
- hình bình hành
- hoặc A B C D có hai đường chéo cắt nhau
- tại I I là trung điểm của mỗi đường AC
- BD thì a b c d cũng là hình bình hành
- nhé
- từ hai dấu hiệu này thì các bạn sẽ trả
- lời cho thầy câu hỏi hỏi chấm 4 tứ giác
- nào dưới đây là hình bình hành và tại
- sao
- chính xác tứ sát đầu tiên là hình bình
- hành bởi vì Theo định lý 2 tứ giác mà
- các cạnh đối bằng nhau là hình bình hành
- tứ giác thứ hai thì không phải là hình
- bình hành bởi vì hai góc đối là góc A và
- góc C không bằng nhau
- còn hình cuối cùng là hình bình hành
- bởi vì a b c d có hai đường chéo acbd
- cắt nhau tại trung điểm của mỗi đường
- Tức là Theo định lý 3 này
- tương tự như thế các bạn sẽ vận dụng hai
- dấu hiệu nhận biết vừa học và hỏi chấm
- năm cho hai điểm A B phân biệt và điểm O
- không nằm trên đường thẳng AB
- gọi a'b' là các điểm sao cho O là trung
- điểm của aa' và bb' chứng minh A phẩy B
- phẩy bằng AB và a'b' song song với AB
- thì chúng ta nhận xét này để mà cặp cạnh
- đối a'b' và AB vừa song song Vừa bằng
- nhau ấy thì thì AB a'b' phải là hình
- bình hành có đúng không nào
- rất chính xác tứ giác
- ab.a'b' có hai đường chéo chính là aa'
- và bb' cắt nhau tại trung điểm O của mỗi
- đường giả thiết cho O là trung điểm của
- cả aa' và bb' mà dẫn tới a b A phẩy B
- phẩy chính là một hình bình hành
- theo định lý 3 mà hình bình hành thì có
- cặp cạnh đối song song và bằng nhau rồi
- dẫn tới A phẩy B phẩy bằng AB và a'b'
- song song với AB ta có chứng minh của
- hỏi chấm 5 vậy bây giờ thầy quay trở lại
- câu hỏi ở phần mở đầu là dịch chuyển êke
- dọc theo đường thẳng D sao cho
- cạnh dài luôn nằm trên đường thẳng d ban
- đầu đỉnh góc 60 độ và đỉnh góc vuông
- trùng với AC sau khi dịch thước thì nó
- trùng với B và D Vậy thì tứ giác ABC thu
- được là hình gì
- như cách vẽ thì do AC và BD cùng chung
- với một cạnh của thước do đó chúng phải
- bằng nhau
- và góc A góc B này cùng bằng 60 độ
- chính xác từ việc góc A và cùng bằng 60
- độ hai góc này lại ở vị trí đồng vị dẫn
- tới AC song song với BD
- hai cạnh đó lại bằng nhau theo giả thiết
- này dẫn tới a b d c là tứ giác có một
- cặp cạnh đối song song bằng nhau Theo
- định lý 2 abdc chính là một hình bình
- hành vậy ta đã có câu trả lời cho phần
- mở đầu và cũng kết thúc cho bài học ngày
- hôm nay của chúng ta như vậy các bạn sẽ
- ghi nhớ cho thầy này chúng ta có các dấu
- hiệu nhận biết hình bình hành như sau
- đầu tiên là sử dụng định nghĩa Nếu tứ
- giác có các cạnh đối song song đó là
- hình bình hành
- thứ hai các cạnh đối của tứ giác bằng
- nhau thì tứ giác là hình bình hành các
- góc đối bằng nhau
- một cặp cạnh đối song song và bằng nhau
- hoặc hai đường chéo cắt nhau tại trung
- điểm mỗi đường thì tứ giác đều là hình
- bình hành các bạn sẽ ghi nhớ cho thầy 5
- dấu hiệu này để phục vụ cho việc chứng
- minh nhé các bài tập luyện tập các bạn
- sẽ làm thêm trên online mới chấm vn để
- chúng ta hiểu bài hơn tới đây bài học
- của chúng ta đã kết thúc thầy Cảm ơn sự
- theo dõi của các em và hẹn gặp lại các
- em trong các bài học tiếp theo trên
- online.vn
OLMc◯2022


Bạn có thể đánh giá bài học này ở đây