Bài tập tự luận: Hình bình hành SVIP

Hướng dẫn giải:

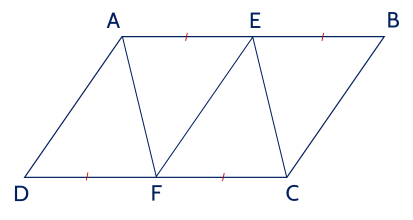
a) Vì ABCD là hình bình hành nên AB = CD, AB // CD.

Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE = $\dfrac12$AB, CF = DF = $\dfrac12$CD

Do đó AE = BE = CF = DF.

Xét tứ giác AEFD có:

     AE // DF (vì AB // CD);

     AE = DF (chứng minh trên)

Do đó tứ giác AEFD là hình bình hành.

Xét tứ giác AECF có:

     AE // CF (vì AB // CD);

     AE = CF (chứng minh trên)

Do đó tứ giác AECF là hình bình hành.

Vậy hai tứ giác AEFD, AECF là những hình bình hành.

b) Vì tứ giác AEFD là hình bình hành nên EF = AD.

Vì tứ giác AECF là hình bình hành nên AF = EC.

Vậy EF = AD, AF = EC.

Hướng dẫn giải:

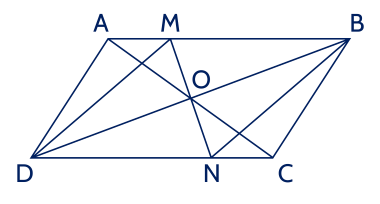
Vì $ABCD$ là hình bình hành nên ta có:

+ Hai đường chéo $AC$ và $BD$ cắt nhau tại $O$ nên $OA = OC$, $OB = OD$.

+ $AB$ // $CD$ nên $AM$ // $CN$ suy ra $\widehat{OAM} = \widehat{OCN}$ (hai góc so le trong).

Xét $\Delta OAM$ và $\Delta OCN$ có:

        $\widehat{O A M} = \widehat{O C N} (chứng minh trên)

        $OA = OC$ (chứng minh trên)

        $\widehat{A O M} = $\widehat{C O N} (hai góc đối đỉnh)

Do đó $\Delta OAM = \Delta OCN$ (g.c.g).

Suy ra $AM = CN$ (hai cạnh tương ứng).

Mặt khác, $AB = CD$ (chứng minh trên);

$AB = AM + BM$; $CD = CN + DN$.

Suy ra $BM = DN$.

Xét tứ giác $MBND$ có:

        $BM$ // $DN$ (vì $AB$ // $CD$)

        $BM = DN$ (chứng minh trên)

Do đó, tứ giác $MBND$ là hình bình hành.

Hướng dẫn giải:

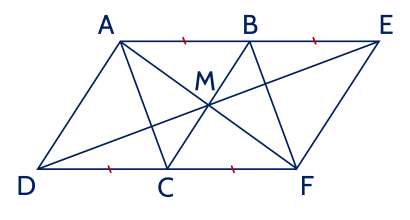
a) Vì ABCD là hình bình hành nên AB = CD; AB // CD.

Mà hai điểm B, C lần lượt là trung điểm AE, DF.

Suy ra AE = DF; AB = BE = CD = CF.

Tứ giác AEFD có AE // DF (vì AB // CD); AE = DF (chứng minh trên).

Do đó tứ giác AEFD là hình bình hành.

Tứ giác ABFC có AB // CF (vì AB // CD); AB = CF (chứng minh trên).

Do đó tứ giác ABFC là hình bình hành.

b) Vì hình bình hành AEFD có hai đường chéo AF và DE nên chúng cắt nhau tại trung điểm của mỗi đường, ta gọi giao điểm đó là O.

Hình bình hành AEFD có hai đường chéo AF và BC.

Mà O là trung điểm của AF.

Suy ra O cũng là trung điểm của BC.

Vậy các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

Hướng dẫn giải:

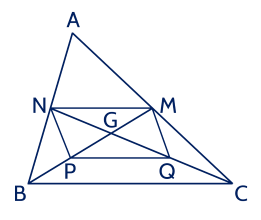
Xét tam giác $ABC$ có hai đường trung tuyến $BM$ và $CN$ cắt nhau tại $G$ (giả thiết) nên $G$ là trọng tâm của $\Delta ABC$.

Suy ra $GM = \dfrac{GB}2$; $GN = \dfrac{GC}2$ (tính chất trọng tâm của tam giác) (1)

Mà $P$ là trung điểm của $GB$ (giả thiết) nên $G P = P B = \dfrac{GB}2$ (2)

$Q$ là trung điểm của $GC$ (giả thiết) nên $G Q = Q C = \dfrac{GC}2$ (3)

Từ (1), (2) và (3) suy ra $GM = GP$ và $GN = GQ$.

Xét tứ giác $PQMN$ có: $GM = GP$ và $GN = GQ$ (chứng minh trên)

Do đó tứ giác $PQMN$ có hai đường chéo $MP$ và $NQ$ cắt nhau tại trung điểm $G$ của mỗi đường nên là hình bình hành.

Hướng dẫn giải:

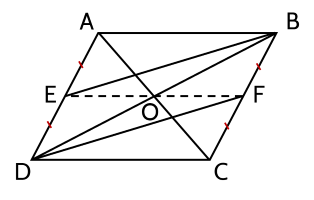
a) ABCD là hình bình hành nên AD = BC và AD // BC.

Mà E là trung điểm của AD nên AE = ED;

F là trung điểm của BC nên BF = FC.

Suy ra DE = BF.

Xét tứ giác EBFD có DE // BF (do AD // BC) và DE = BF nên là hình bình hành (dấu hiệu nhận biết).

b) Ta có O là giao điểm của hai đường chéo của hình bình hành ABCD nên O là trung điểm của BD.

Do EBFD là hình bình hành nên hai đường chéo BD và EF cắt nhau tại trung điểm của mỗi đường.

Mà O là trung điểm của BD nên O là trung điểm của EF.

Vậy ba điểm E, O, F thẳng hàng.

Hướng dẫn giải:

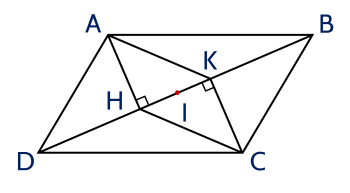
a) Do $ABCD$ là hình bình hành nên $AD$ // $BC$ và $AD = BC$.

Do $AD$ // $BC$ nên $\widehat{ADB} = \widehat{CBD}$ (so le trong)

Xét $\Delta ADH$ và $\Delta CBK$ có:

     $\widehat{AHD} = \widehat{CKB}= 90^\circ$;

     $AD = BC$ (chứng minh trên);

     $\widehat{ADH} = \widehat{CBK}$ (do $\widehat{ADB} = \widehat{CBD}$).

Do đó $\Delta ADH = \Delta CBK$ (cạnh huyền – góc nhọn).

Suy ra $AH = CK$ (hai cạnh tương ứng).

Ta có $AH \perp DB$ và $CK \perp DB$ nên $AH$ // $CK$.

Tứ giác $AHCK$ có $AH$ // $CK$ và $AH = CK$ nên $AHCK$ là hình bình hành (dấu hiệu nhận biết).

b) Do $AHCK$ là hình bình hành (câu a) nên hai đường chéo $AC$ và $HK$ cắt nhau tại trung điểm của mỗi đường.

Mà $I$ là trung điểm của $HK$ (giả thiết) nên $I$ là trung điểm của $AC$.

Do $ABCD$ là hình bình hành nên hai đường chéo $AC$ và $BD$ cắt nhau tại trung điểm của mỗi đường.

Mà $I$ là trung điểm của $AC$ nên $I$ là trung điểm của $BD$, hay $IB = ID$.