Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài toán liên quan đến hai đường tròn cắt nhau SVIP
Cho hai đường tròn $(O;12$ cm$)$ và $(O';5$ cm$)$, $OO'=13$ cm.
a) Chứng minh rằng hai đưòng tròn $(O)$ và $(O')$ cắt nhau tại hai điểm phân biệt.
b) Gọi $A, \, B$ là giao điểm của hai đường tròn $(O)$ và $(O')$. Chứng minh rằng $OA$ là tiếp tuyến của đường tròn $(O')$, $O'A$ là tiếp tuyến của đường tròn $(O)$. Tính độ dài $AB$.
Hướng dẫn giải:
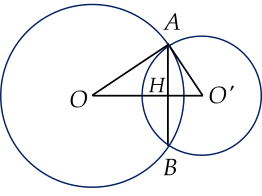
a) Ta có: $12-5<13<12+5$ hay $R-R'<d<R+R'$ nên hai đường tròn $(O)$ và $(O')$ cắt nhau tại hai điểm phân biệt
b) $OA^2+O'A^2=12^2+5^2=169$;
$O'O^2=13^2=169$
$\Delta OAO'$ có: $OA^2+O'A^2=O'O^2$, theo định lí Pythagore đảo suy ra tam giác $\Delta OAO'$ vuông tại $A$.
Có $OA \bot O'A$ do đó $OA$ là tiếp tuyến của đường tròn $(O')$ và $O'A$ là tiếp tuyến của đường tròn $(O)$.
$O'O$ là đường trung trực của đoạn $AB$.
Gọi $H$ là giao điểm của $O'O$ và $AB$ nên $AH.O'O=OA.O'A$ suy ra $AH=\dfrac{OA.O'A}{O'O}=\dfrac{12.5}{13}=\dfrac{60}{13}$ cm.
Vậy $AB=2AH=\dfrac{120}{13}$ cm.
Cho hai đường tròn $(O)$ và $(O')$ cắt nhau ở $A$ và $B$, ($O$ và $O'$ thuộc hai nửa mặt phẳng bờ $AB$). Kẻ các đường kính $BOC$ và $BO'D$.
a) Chứng minh rằng ba điểm $C$, $A$, $D$ thẳng hàng.
b) Biết $OO'=5$ cm, $OB=4$ cm, $O'B=3$ cm. Tính diện tích tam giác $BCD$.
Hướng dẫn giải:

a) $\Delta BCD$ có $OO'$ là đường trung bình suy ra $OO'$ // $CD$ (1)
$\Delta ABC$ có $OI$ là đường trung bình suy ra $OO'$ // $CA$ (2)
Từ (1) và (2) suy ra $C$, $A$, $D$ thẳng hàng.
b) Ta có: $\Delta OBO'$ vuông tại $B$ suy ra $\Delta BCD$ vuông tại $B$
Suy ra $S_{BCD}=\dfrac12.BC.BD=\dfrac{1}{2}.8.6=24$ (cm$^{2}$).
Cho hai đường tròn $(O)$ và $(O')$ giao nhau tại $M$ và $N$. Gọi $I$ là trung điểm của $OO'$. Đường thẳng kẻ qua $M$ vuông góc $MI$ cắt đường tròn $(O)$ và $(O')$ lần lượt ở $A$ và $B$. Hai đường thẳng vuông góc với $AB$ tại $A$ và $B$ cắt đường tròn $(O)$ ở $P$, $(O')$ ở $Q$
a. Chứng minh rằng $M$ là trung điểm của $AB$.
b. $MI$ cắt $PQ$ ở $E$, chứng minh $EP=EQ$.
c. Chứng minh $IH=IK$.
Hướng dẫn giải:
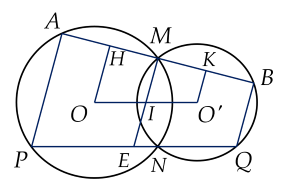
a. Kẻ $OH \bot AM$; $O'K \bot MB$ suy ra $OH$ // $O'K$.
Tứ giác $HKOO'$ là hình thang, $MI \bot AB$ suy ra $MI$ // $OH$ và $IO$ // $IO'$
Suy ra $MH=MK$.
Mà $OH \bot AM$ suy ra $HA=HM=MK=KB$ (đpcm).
b. Ta có $ME$ là đường trung bình của hình thang $ABQP$
Suy ra $EP=EQ$.
c. Xét $\Delta HIK$, có $IM$ là đường trung tuyến đồng thời là đường cao.
Suy ra $\Delta HIK$ cân tại $I$ (đpcm).
Cho góc vuông $xOy$. Lấy các điểm $I$ và $K$ lần lượt trên các tia $Ox, \, Oy$. Đường tròn $( I;OK)$ cắt tia $Ox$ tại $M$ ($I$ nằm giữa $O$ và $M$), đường tròn $( K;OI )$ cắt tia $Oy$ tại $N$ ($K$ nằm giữa $O$ và $N$)
a. Chứng minh $(I)$ và $(K)$ luôn cắt nhau.
b. Tiếp tuyến tại $M$ của $(I)$, tiếp tuyến tại $N$ của $(K)$ cắt nhau tại $C$. Chứng minh tứ giác $OMCN$ là hình vuông.
c. Gọi $A, \, B$ là các giao điểm của $(I)$ và $(K)$ trong đó $B$ ở miền trong góc $xOy$. Chứng minh ba điểm $A, \, B, \, C$ thẳng hàng.
d. Giả sử $I$ và $K$ theo thứ tự đi động trên các tia $Ox$ và $Oy$ sao cho $OI+OK=a$ không đổi. Chứng minh đường thẳng $AB$ luôn đi qua một điểm cố định.
Hướng dẫn giải:
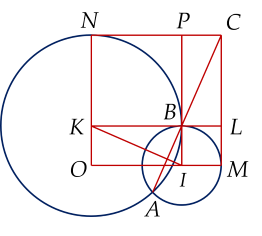
a. $| OI-OK |<IK<OI+OK$ suy ra $( I )$ và $( K )$ luôn cắt nhau
b. Do $OI=NK$; $OK=IM$ suy ra $OM=ON$,
Mà $OMCN$ là hình chữ nhật nên $OMCN$ là hình vuông.
c. Gọi $L$ là giao điểm của $KB$ và $MC$; $P$ là giao điểm của $IB$ và $NC$
Suy ra $OBKI$ là hình chữ nhật và $BLMI$ là hình vuông nên $\Delta BLC=\Delta KIO$
Suy ra $\widehat{LBC}=\widehat{OKI}=\widehat{BIK}$
Mà $\widehat{BIK}+\widehat{IBA}=90^\circ$ suy ra $\widehat{LBC}+\widehat{IBA}=90^\circ$
Do đó, $\widehat{LBC}+\widehat{LBI}+\widehat{IBA}=180^\circ$.
d. Có $OMCN$ là hình vuông cạnh $a$ cố định nên $C$ cố định và $AB$ luôn đi qua $C$.
