Bài tập tự luận: Định lí Thalès trong tam giác SVIP

Hướng dẫn giải:

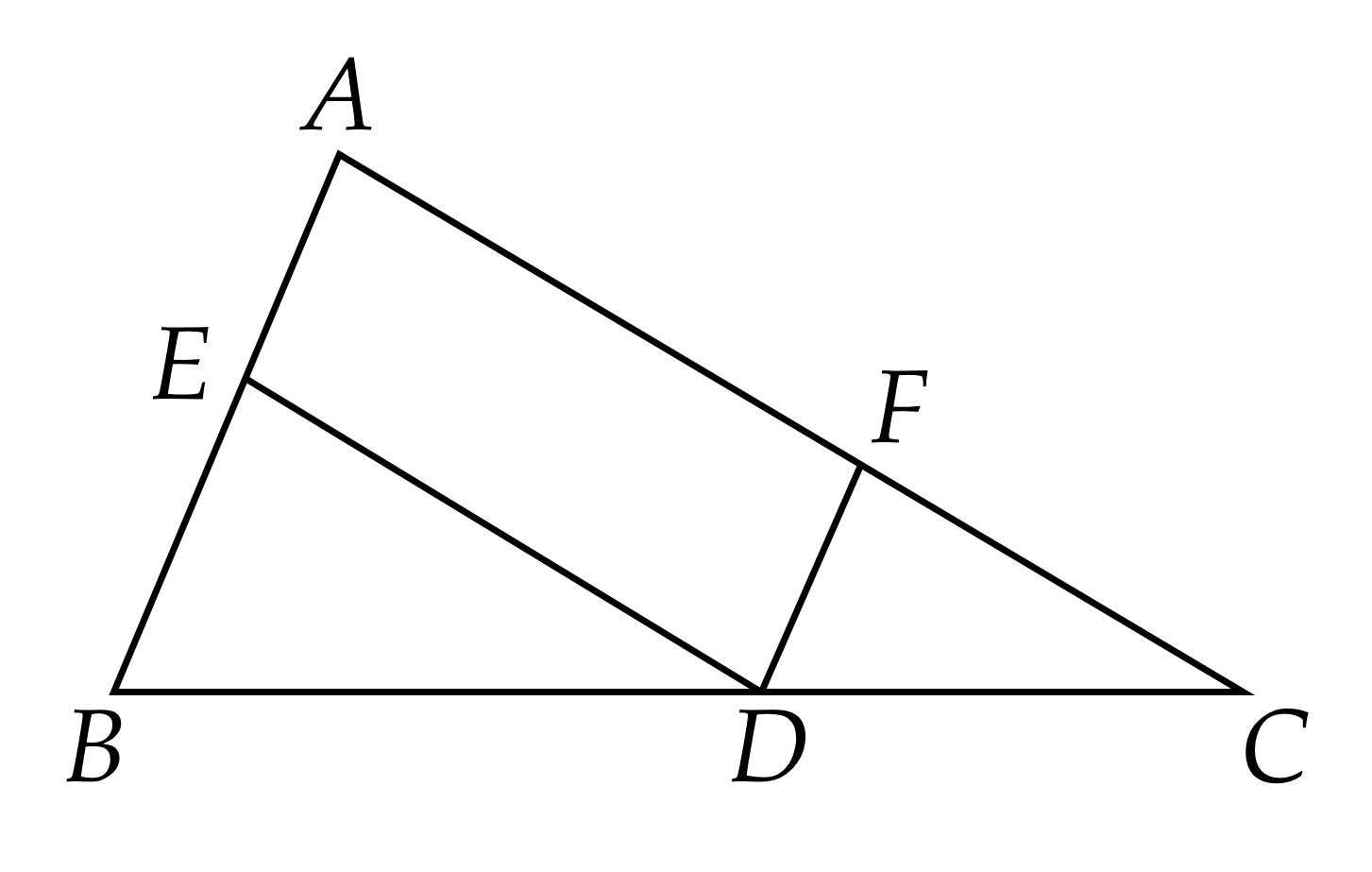
Áp dụng định lí Thalès trong tam giác:

⚡$DE$ // $AC$ nên $\dfrac{A E}{A B}=\dfrac{C D}{B C}$;

⚡$DF$ // $AC$ nên $\dfrac{A F}{A C}=\dfrac{B D}{B C}$.

Khi đó, $\dfrac{A E}{A B}+\dfrac{A F}{A C}=\dfrac{C D}{B C}+\dfrac{B D}{B C}=\dfrac{B C}{B C}=1$.

Hướng dẫn giải:

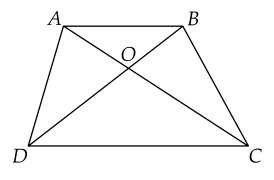
$ABCD$ là hình thang suy ra $AB$ // $CD$.

Áp dụng hệ quả định lí Thalès, ta có: $\dfrac{OA}{OC} = \dfrac{OB}{OD} $

Suy ra $O A . O D = O B . O C$ (đpcm).

Hướng dẫn giải:

Lấy $D$ là trung điểm của cạnh $BC$.

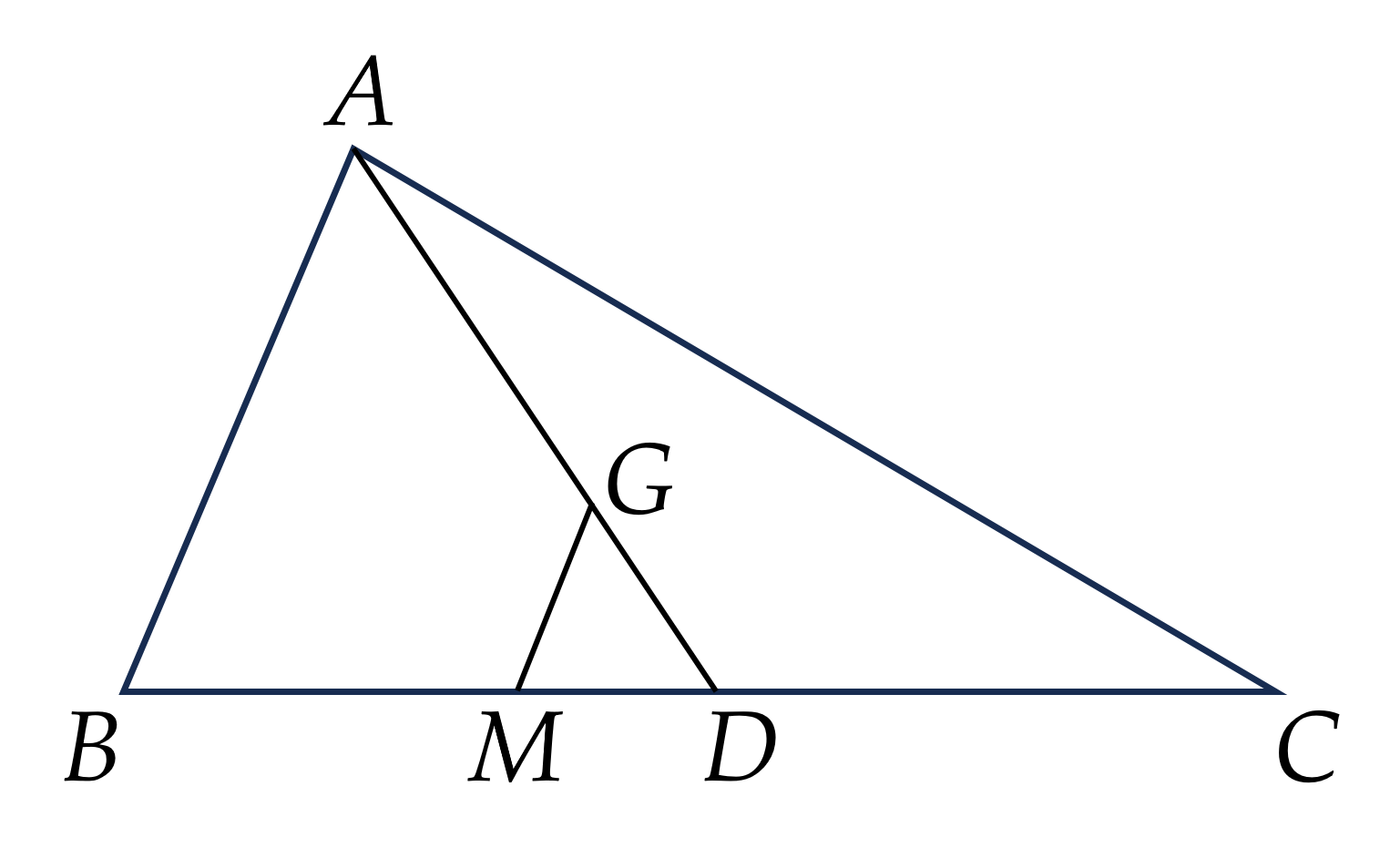
Khi đó, $A D$ là đường trung tuyến của tam giác $A B C$.

Vì $G$ là trọng tâm của tam giác $A B C$ nên điểm $G$ nằm trên cạnh $A D$.

Ta có $\dfrac{A G}{A D}=\dfrac{2}{3}$ hay $A G=\dfrac{2}{3} A D$.

Vì $MG$ // $AB$, theo định lí Thalès, ta suy ra: $\dfrac{A G}{A D}=\dfrac{B M}{B D}=\dfrac{2}{3}$.

Ta có $BD=CD$ (vì $D$ là trung điểm của cạnh $BC$) nên $\dfrac{B M}{B C}=\dfrac{B M}{2 B D}=\dfrac{2}{2 . 3}=\dfrac{1}{3}$.

Do đó $B M=\dfrac{1}{3} B C$ (đpcm).

Hướng dẫn giải:

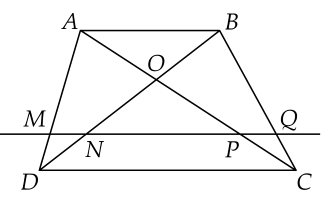
Trong tam giác $ADB$, ta có: $MN$ // $AB$ (gt)

Suy ra $\dfrac{DN}{DB} = \dfrac{MN}{AB}$ (hệ quả định lí Thalès) (1)

Trong tam giác $ACB$, ta có: $PQ$ // $AB$ (gt)

Suy ra $\dfrac{CQ}{CB} = \dfrac{PQ}{AB}$ (hệ quả định lí Thalès) (2)

Lại có: $NQ$ // $AB$ (gt); $AB$ // $CD$ (gt)

Suy ra $NQ$ // $CD$

Trong tam giác $BDC$, ta có: $NQ$ // $CD$ (chứng minh trên)

Suy ra $\dfrac{DN}{DB} = \dfrac{CQ}{CB}$ (định lí Thalès) (3)

Từ (1), (2) và (3) suy ra $\dfrac{MN}{AB} = \dfrac{PQ}{AB} hay $MN = PQ$ (đpcm).

Hướng dẫn giải:

Xét tam giác $ABC$ có $BC \perp AB'$ và $B'C' \perp AB'$ nên suy ra $BC$ // $B'C'$.

Theo hệ quả định lí Thalès, ta có: $\dfrac{AB}{AB'} = \dfrac{BC}{BC'}$

Suy ra $\dfrac{x}{x + h} = \dfrac a{a'}$

$a'.x = a ( x + h ) $

$a'.x − a x = a h$

$x ( a' − a ) = a h$

$x = \dfrac {ah }{a' − a}$.