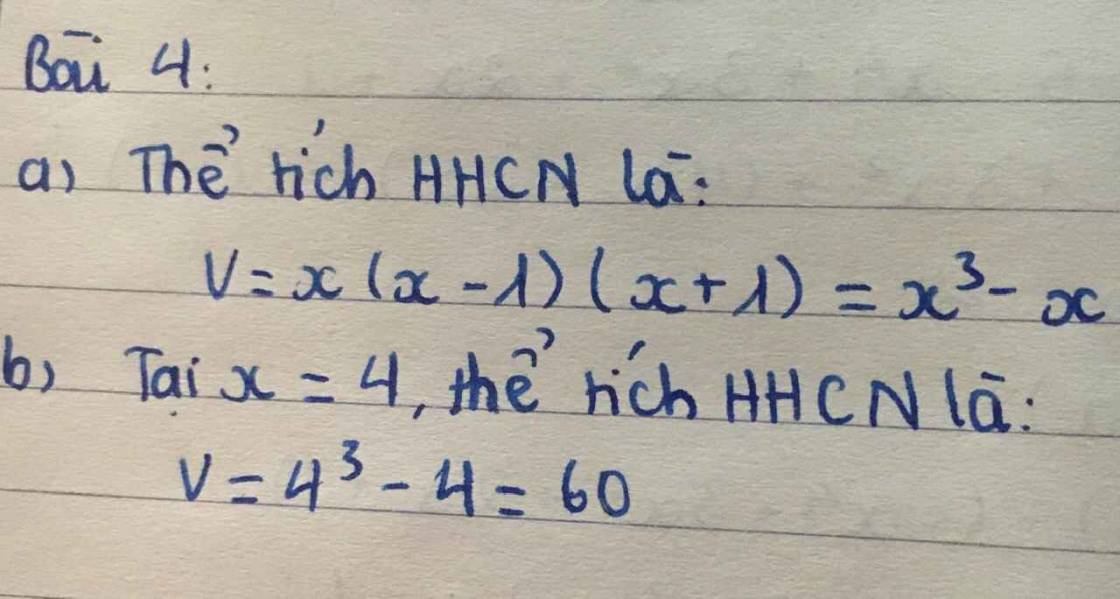
a) Xét hai tam giác BADBAD và BFDBFD có:

     ABD^ = FBD^ABD = FBD

(vì BDBD là tia phan giác của góc BB);

     AB = BF AB = BF (ΔABFΔABF cân tại BB);

     BDBD là cạnh chung;

Vậy ΔBAD = ΔBFD ΔBAD = ΔBFD (c.g.c).

b) ΔBAD = Δ BFDΔBAD = Δ BFD suy ra BAD^ = BFD^ = 100∘BAD

= BFD

= 100∘ (hai góc tương ứng).

Suy ra DFE^ = 180∘−BFD^ = 80∘DFE

=180∘ − BFD

=80∘. (1)

Tam giác ABCABC cân tại AA nên B^ = C^ =  180∘−100∘2 = 40∘B

= C

= 2180∘−100∘ ​= 40∘

Suy ra DBE^ = 20∘DBE

= 20∘.

Tương tự, tam giác BDEBDE cân tại BB nên BED^ = 180∘−20∘2 = 80∘BED

= 2180∘−20∘​ = 80∘. (2)

Từ (1) và (2) suy ra ΔDEFΔDEF cân tại D.

Gọi số máy cày của ba đội lần lượt là �$x$, �$y$, �$z$ (máy).

Vì diện tích cày là như nhau nên số máy cày và thời gian là hai đại lượng tỉ lệ nghịch.

Nên  �.5=�.6=�.8⇒�24=�20=�15x.5 = y.6 = z.8⇒

​ x / 24 = y/20 = z/ 15

Đội thứ hai có nhiều hơn đội thứ ba 5$5$ máy nên �−�=5$y-z=5$.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

�24=�20=�15=�−�20−15=55=1x/24 = y/ 25 = x/ 15 = y - z / 20 - 15 = 5/5 = 1

Suy ra  �=24$x=24$ �=20$;\; y=20$ ; �=15$z=15$.

                    x3  - 3x2 +  x + 1

              -   2x3 -   x2 + 3x - 4

              _________________

               -x3  -  2x2 - 2x + 5 

P(x) - Q(x) = -x3 - 2x2 - 2x + 5

b, Thay x = 1 vào P(x); Q(x) ta có : 

P(1) = 13 - 3.12 + 1 + 1 = 0  

Q(1) = 2.13 - 12 + 3.1 - 4 = 0

Vậy 1 là nghiệm của cả hai đa thức P(x) và Q(x)

a) x/-4 = - 11/ 2                                         b) 15 - x / x + 9 = 3/5

x = (- 11) . (- 4) / 2                                        ( 15 - x ) . 5 = ( x + 9 ). 3

x = 22                                                            75 - 5x  = 3x + 27 

                                                                        8x = 48          x = 6