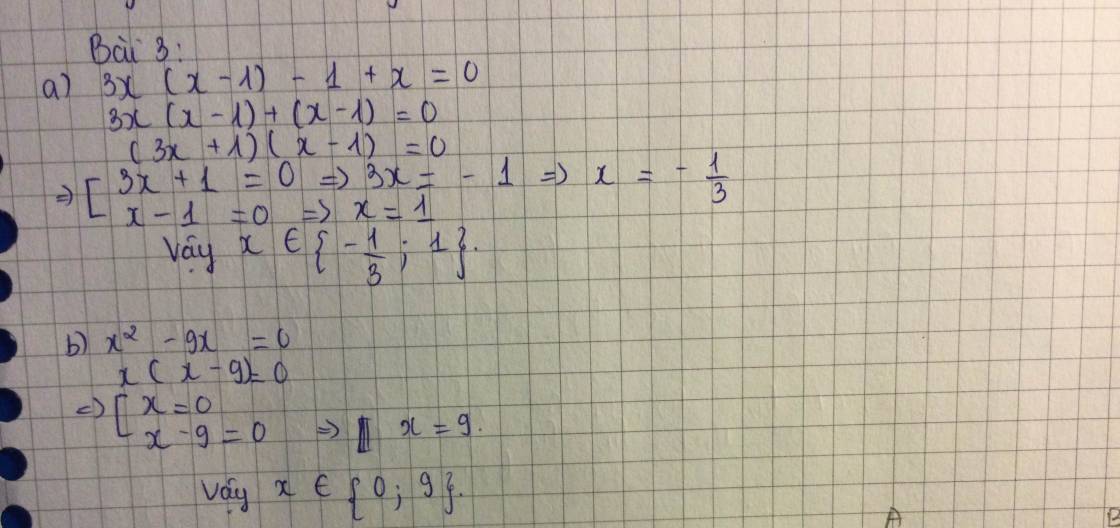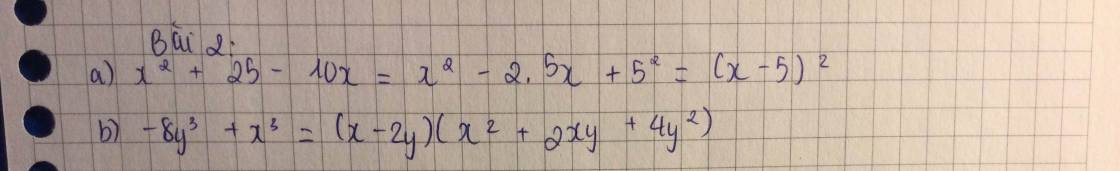Lâm Thị Thảo
Giới thiệu về bản thân



































Do AB//CD( vì cùng vuông góc với BD)
Nên áp dụng định lí Ta lét , ta được :
EB/ED=AB/CD
=> EB/6 = 150/4
=> EB = 150.6/4 = 225 (cm)
a) x - 3 = (3 - x)²
x - 3 = (x - 3)²
x - 3 - (x - 3)² = 0
(x - 3)[1 - (x - 3)] = 0
(x - 3)(1 - x + 3) = 0
(x - 3)(4 - x) = 0
x - 3 = 0 hoặc 4 - x = 0
*) x - 3 = 0
x = 3
*) 4 - x = 0
x = 4
Vậy x = 3; x = 4
b) x³ + 3/2 x² + 3/4 x + 1/8 = 1/64
(x + 1/2)³ = 1/64
(x + 1/2)³ = (1/4)³
x + 1/2 = 1/4
x = 1/4 - 1/2
x = -1/2
a) x² + 2xy + y² - x - y
= (x² + 2xy + y²) - (x + y)
= (x + y)² - (x + y)
= (x + y)(x + y + 1)
b) 2x³ + 6x² + 12x + 8
= 2(x³ + 3x² + 6x + 4)
= 2(x³ + x² + 2x² + 2x + 4x + 4)
= 2[(x³ + x²) + (2x² + 2x) + (4x + 4)]
= 2[x²(x + 1) + 2x(x + 1) + 4(x + 1)]
= 2(x + 1)(x² + 2x + 4)
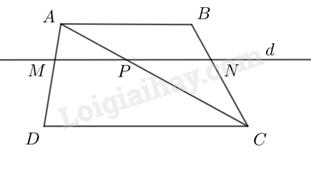
a) Vì
d
∥
C
D
𝑑
∥
𝐶
𝐷
nên
M
P
∥
C
D
𝑀
𝑃
∥
𝐶
𝐷
Xét tam giác ADC với
M
P
∥
C
D
𝑀
𝑃
∥
𝐶
𝐷
có:
A
M
M
D
=
A
P
P
C
(
1
)
𝐴
𝑀
𝑀
𝐷
=
𝐴
𝑃
𝑃
𝐶
(
1
)
(Định lý Thales)
Vì
d
∥
A
B
𝑑
∥
𝐴
𝐵
nên
P
N
∥
A
B
𝑃
𝑁
∥
𝐴
𝐵
Xét tam giác ABC với
P
N
∥
A
B
𝑃
𝑁
∥
𝐴
𝐵
có:
B
N
N
C
=
A
P
P
C
(
2
)
𝐵
𝑁
𝑁
𝐶
=
𝐴
𝑃
𝑃
𝐶
(
2
)
(Định lý Thales)
Từ (1) và (2) ta có
A
M
M
D
=
B
N
N
C
𝐴
𝑀
𝑀
𝐷
=
𝐵
𝑁
𝑁
𝐶
.
b) Vì
M
D
=
2
M
A
𝑀
𝐷
=
2
𝑀
𝐴
nên
A
M
M
D
=
1
2
⇒
A
M
A
D
=
1
3
𝐴
𝑀
𝑀
𝐷
=
1
2
⇒
𝐴
𝑀
𝐴
𝐷
=
1
3
Xét tam giác ADC với
M
P
∥
C
D
𝑀
𝑃
∥
𝐶
𝐷
có:
A
M
A
D
=
M
P
D
C
𝐴
𝑀
𝐴
𝐷
=
𝑀
𝑃
𝐷
𝐶
(Hệ quả định lý Thales)
⇒
M
P
D
C
=
1
3
⇒
M
P
=
1
3
D
C
=
2
c
m
⇒
𝑀
𝑃
𝐷
𝐶
=
1
3
⇒
𝑀
𝑃
=
1
3
𝐷
𝐶
=
2
𝑐
𝑚
Vì
A
M
A
D
=
1
3
⇒
A
P
A
C
=
1
3
⇒
P
C
C
A
=
2
3
𝐴
𝑀
𝐴
𝐷
=
1
3
⇒
𝐴
𝑃
𝐴
𝐶
=
1
3
⇒
𝑃
𝐶
𝐶
𝐴
=
2
3
Xét tam giác ABC với
P
N
∥
A
B
𝑃
𝑁
∥
𝐴
𝐵
có:
C
P
C
A
=
P
N
A
B
𝐶
𝑃
𝐶
𝐴
=
𝑃
𝑁
𝐴
𝐵
(Hệ quả định lý Thales)
⇒
P
N
A
B
=
2
3
⇒
P
N
=
2
3
A
B
=
8
3
c
m
⇒
𝑃
𝑁
𝐴
𝐵
=
2
3
⇒
𝑃
𝑁
=
2
3
𝐴
𝐵
=
8
3
𝑐
𝑚
Mà
M
N
=
M
P
+
P
M
=
2
+
8
3
=
14
3
c
m
𝑀
𝑁
=
𝑀
𝑃
+
𝑃
𝑀
=
2
+
8
3
=
14
3
𝑐
𝑚
.
a) 5000
b) 1
Lời giải:
Vậy .
Giá trị này đạt tại