

Phạm Thảo Nguyên
Giới thiệu về bản thân



































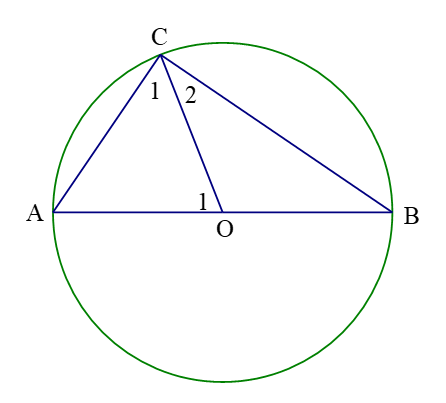
Tam giác có ba cạnh bằng nhau nên là tam giác đều
Suy ra .
Ta có: có nên cân tại suy ra ;
là góc ngoài của .
Do đó
Vậy .
có trung tuyến bằng nửa cạnh đối xứng nên vuông tại với
Suy ra và
Vậy có .
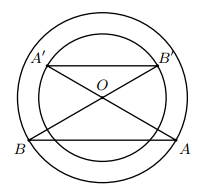
a) Từ giả thiết, ta có ;
.
Suy ra .
b) Vì nên theo hệ quả của định lí Thalès ta có:
// .
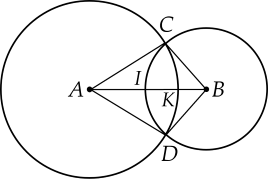
a) Hai đường tròn cm và cm cắt nhau tại và nên cm, cm.
b) cm, cm.
Suy ra cm.
Điểm là trung điểm của đoạn thẳng .
c) Ta có: cm nên cm.

a) Hai đường tròn cm và cm cắt nhau tại và nên cm, cm.
b) cm, cm.
Suy ra cm.
Điểm là trung điểm của đoạn thẳng .
c) Ta có: cm nên cm.
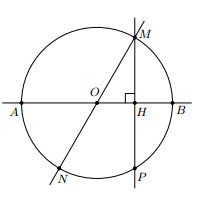
a) Do là tâm đối xứng của nên điểm đối xứng với điểm qua tâm phải vừa thuộc , vừa thuộc .
Vậy là giao điểm của đường thẳng với .
b) Do là trục đối xứng của nên điểm đối xứng với điểm qua phải vừa thuộc , vừa thuộc đường thẳng vuông góc hạ từ xuống .
Vậy là giao điểm của với đường thẳng đi qua và vuông góc với .
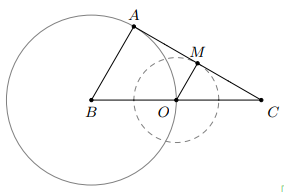
a) Điểm cố định. Điểm cách một khoảng là cm nên nằm trên đường tròn cm.
b) Gọi là trung điểm của thì là một điểm cố định.
Ta có cm.
Điểm cách điểm một khoảng cm nên nằm trên đường tròn cm.
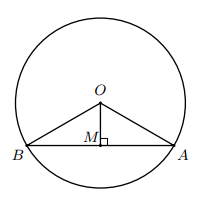
a) Ta có cân tại vì .
Mà là trung điểm của nên là đường trung tuyến của tam giác .
Khi đó cũng là đường trung trực của đoạn thẳng .
b) Khoảng cách từ điểm đến đường thẳng chính là đoạn thẳng .
là trung điểm của nên cm.
Xét vuông tại , có (định lí Pythagore).
Suy ra cm.
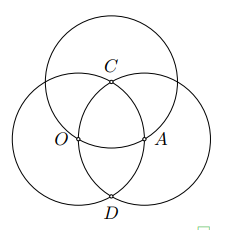
b) Đường tròn cm và cm cắt nhau tại , , điểm nằm trên đường tròn tâm nên:
cm, cm.
Suy ra cm.
Do đó đường tròn cm đi qua hai điểm và .