

Phạm Thảo Nguyên
Giới thiệu về bản thân



































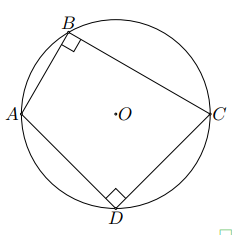
Tứ giác có nên (đường cao ứng với cạnh huyền).
Suy ra bốn điểm , , , cùng nằm trên một đường tròn tâm , đường kính .
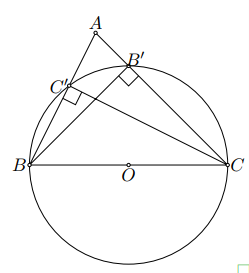
Tam giác có hai đường cao và nên
Suy ra (đường cao ứng với cạnh huyền).
Do đó bốn điểm , , , cùng nằm trên một đường tròn.
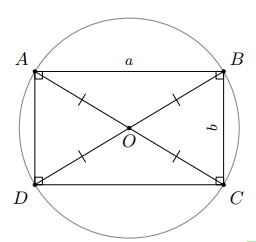
Gọi là giao điểm của hai đường chéo và .
Theo tính chất hai đường chéo của hình chữ nhật, ta có .
Vậy bốn điểm , , , cùng thuộc .
Áp dụng định lí Pythagore vào tam giác vuông , ta có:
Do đó .
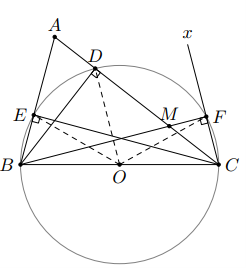
Gọi là trung điểm của .
Ta có là đường cao nên , hay tam giác vuông tại .
Trong tam giác vuông có là trung tuyến ứng với cạnh huyền nên:
Tương tự ta có:
Và
Từ , và suy ra .
Do đó năm điểm , , , , cùng thuộc một đường tròn.
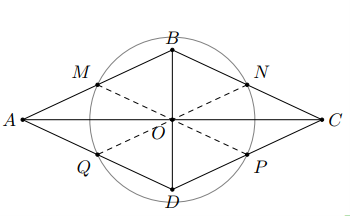
Gọi , , , lần lượt là trung điểm của bốn cạnh , , và của hình thoi .
Gọi là giao điểm của và .
Ta có .
Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông, ta được:
; ;
;
Mặt khác nên .
Do đó bốn điểm , , , cùng nằm trên một đường tròn.
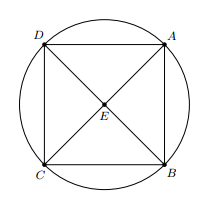
a) Vì hình vuông có tâm suy ra .
Do đó, các điểm , , và cùng thuộc một đường tròn tâm .
Hai trục đối xứng của đường tròn là và .
b) Cạnh hình vuông bằng cm nên áp dụng định lí Pythagore, ta có:
suy ra .
Vậy bán kính của đường tròn là cm.
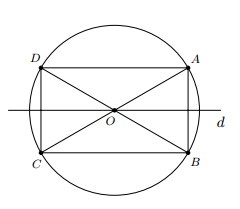
a) Giả sử đường tròn có bán kính suy ra
Do là điểm đối xứng với qua suy ra
Do là điểm đối xứng với qua suy ra
Do là điểm đối xứng với qua suy ra
Từ , , và suy ra , và cùng thuộc .
b) Ta thấy và cắt nhau tại là trung điểm của mỗi đường, suy ra là hình chữ nhật.
c) Ta thấy suy ra là đường trung trực của .
Suy ra và đối xứng với nhau qua .
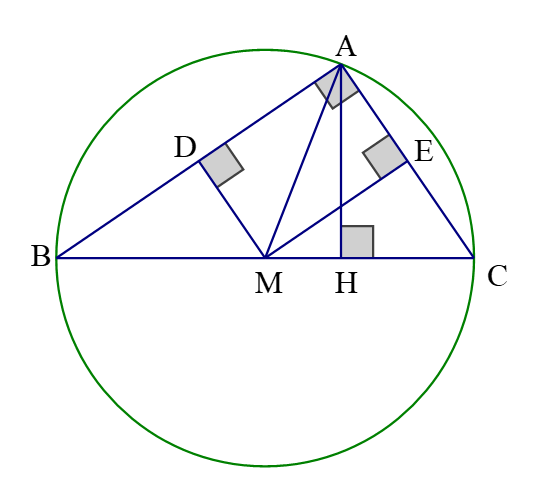
Vì ba tam giác có chung cạnh huyền nên ba đỉnh góc vuông nằm trên đường tròn đường kính có tâm là trung điểm của .
Vậy năm điểm cùng nằm trên một đường tròn.
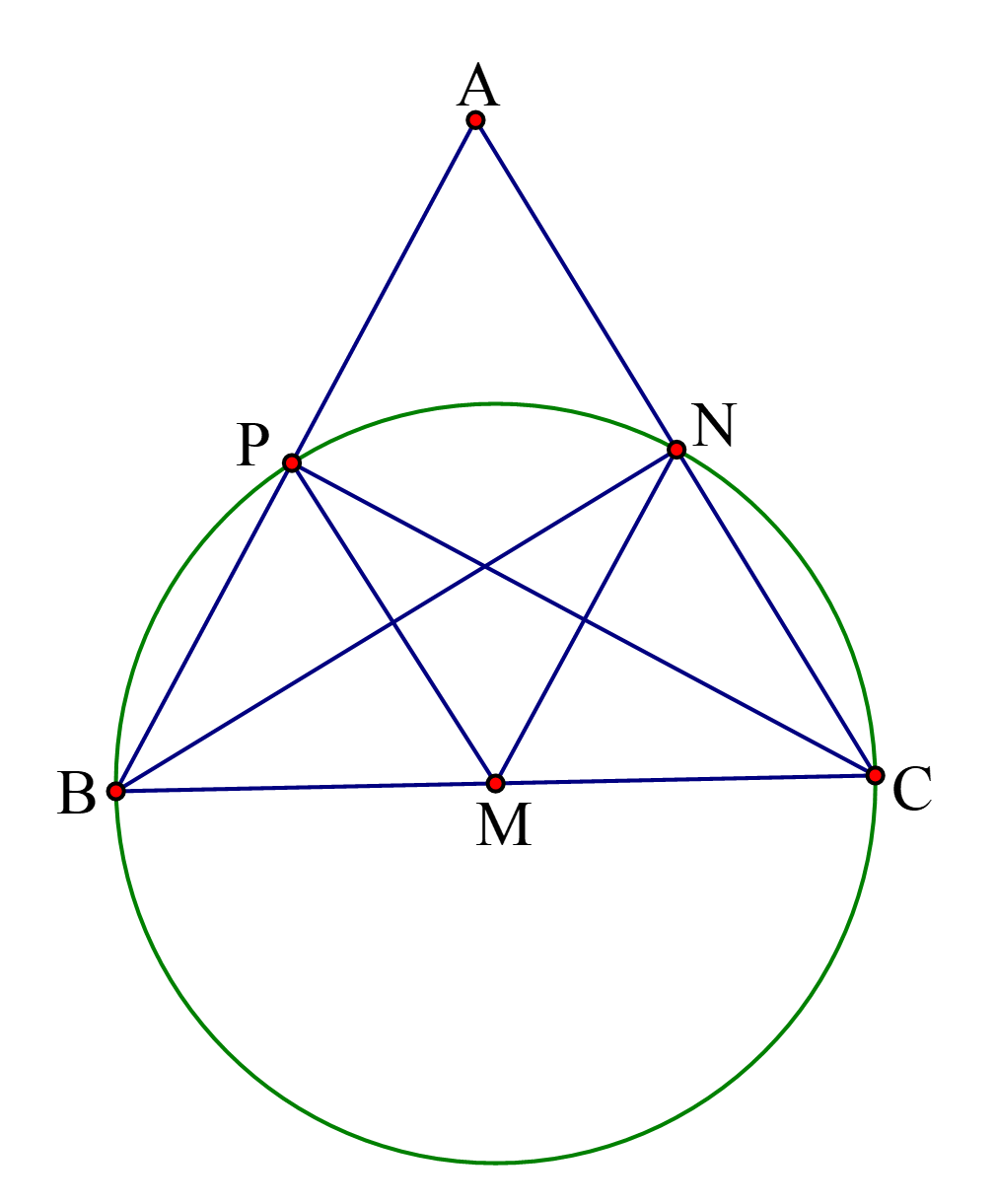
Vì tam giác đều nên các trung tuyến đồng thời cũng là đường cao.
Suy ra lần lượt vuông góc với .
là tam giác vuông, có là cạnh huyền nên (1)
là tam giác vuông, có là cạnh huyền nên (2)
Từ (1) và (2) suy ra hay các điểm cùng thuộc đường tròn, đường kính , tâm đường tròn là trung điểm của .
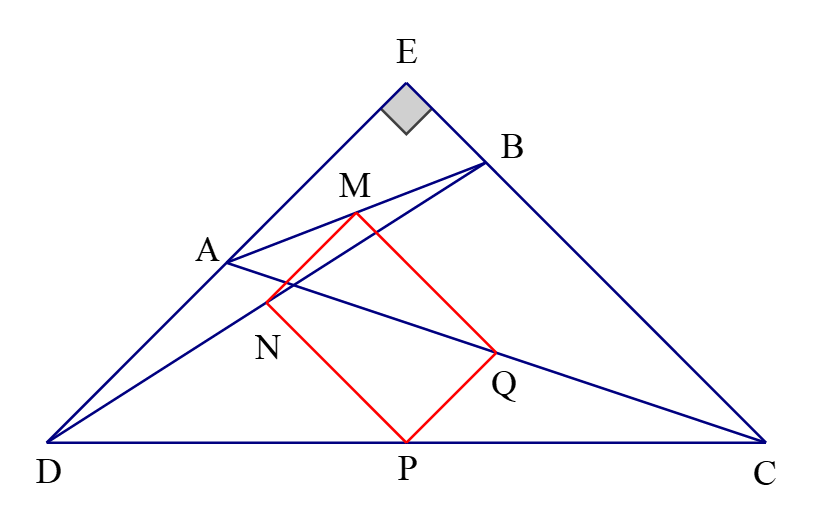
Xét tứ giác , ta có: // và // suy ra là hình bình hành.
Kéo dài và cắt nhau tại .
Ta có: suy ra .
Lại có: // và // suy ra
Do đó là hình chữ nhật suy ra nằm trên một đường tròn với tâm là giao điểm của hai đường chéo của hình chữ nhật, bán kính bằng nửa đường chéo.