Luận điểm 1: Khổ thơ đầu thể hiện khát vọng được cống hiến của nhà thơ.
"Ta làm con chim hót,
 Ta làm một cành hoa
 Ta nhập vào hòa ca,
 Một nốt trầm xao xuyến"
- Khổ thơ sử dụng phép điệp từ với từ "Ta làm" cùng nhịp thơ nhanh, dồn dập => Thể hiện khát vọng mãnh liệt được cống hiến của nhà thơ.
\(\cdot\) Làm con chim hót: góp tiếng hót, âm thanh tươi mới, hân hoan cho đời.
\(\cdot\) Làm một cành hoa: góp hương thơm, sắc thắm cho đời, điểm to cho cuộc sống.
=> Đó là những ước mơ vô cùng nhỏ bé, đơn sơ, tô điểm cho mùa xuân của đất nước.
+ Một nốt trầm: một âm trầm, không ồn ào, không nổi bật, không cao điệu, chỉ âm thầm lặng lẽ nhập vào khúc ca đón mừng xuân về của nhân dân.
- Nhà thơ sử dụng đại từ "ta" chính là muốn nói đây không phải chỉ là tâm niệm riêng của ông, mà nó còn là khát vọng chung của một dân tộc.
=> Khổ thơ đã thể hiện rõ nét khát vọng được nhập vào cuộc đời, được cống hiến một phần tốt đẹp, dù nhỏ bé, của mình cho cuộc đời chung, nguyện vì sự phồn vinh của dân tộc mà hi sinh mình. Đây chính là tâm niệm cao đẹp, đáng quý của một nhà cách mạng, một nhà thơ đã sống trọn nhịp thở với đất nước, với quê hương.

Luận điểm 2: Khổ thơ cuối đoạn thể hiện ước nguyện được cống hiến chân thành, tha thiết, không kể tuổi tác.
"Một mùa xuân nho nhỏ
 Lặng lẽ dâng cho đời
 Dù là tuổi hai mươi
 Dù là khi tóc bạc."
\(\cdot\) "Mùa xuân nho nhỏ" là một hình ảnh ẩn dụ cho cuộc đời của mỗi con người, thể hiện cho mỗi một sự cống hiến thầm lặng => Nhà thơ muốn được góp một phần công sức nhỏ bé của mình để điểm tô cho mùa xuân vĩ đại của đất nước.
\(\cdot\) Nhà thơ đã sử dụng các từ láy "lặng lẽ", "nho nhỏ", đây là một cách nói khiêm tốn và chân thành của nhân cách sống cao đẹp khi luôn muốn góp vào lợi ích chung của dân tộc.
=> Nhà thơ có một cách sống đẹp, đó là một lẽ sống cống hiến khiêm tốn, lặng lẽ, âm thầm, không mong cầu được tôn vinh.
\(\cdot\) Điệp ngữ "dù là" thể hiện thái độ tự tin, cứng cỏi trước mọi khó khăn của cuộc đời.
\(\cdot\) "Tuổi hai mươi", "khi tóc bạc": sự cống hiến âm thầm bất kể tuổi tác, bất kể thời gian, bất kể khi còn hăng hái hay đã sắp cạn sức lực, vẫn muốn đóng góp mọi thứ của mình cho sự nghiệp chung.
-> Đây chính là lời tự nhủ bản thân phải kiên trì, phải quật cường dẫu cho thời gian có thể cướp đi sức trẻ của con người, để có thể mãi là một mùa xuân nho nhỏ trong mùa xuân lớn của quên hương.
Đánh giá
Nhà thơ thành công trong việc sử dụng thể thơ năm chữ, hình ảnh thơ giản dị, trong sáng, giọng thơ nhẹ nhàng, sâu lắng, tha thiết, giàu hình ảnh, giàu nhạc điệu, ẩn dụ, điệp ngữ, đoạn thơ thể hiện điều tâm niệm thật chân thành, tha thiết của nhà thơ. Thanh Hải đã vượt lên cả bệnh tật, tuổi già bằng một niềm yêu đời tha thiết, mãnh liệt để luôn hướng mình đến lối sống có ích cho đời.

\(b\)) \(x^2-\left(2m+1\right)x+m^2-1=0\) \(\left(1\right)\)
Ta có: \(\Delta=b^2-4ac=\left[-\left(2m+1\right)\right]^2-4\cdot1\cdot\left(m^2-1\right)\)
\(=4m^2+4m+1-4m^2+4\)
\(=4m+5\)
Để phương trình có hai nghiệm \(x_1,x_2\) thì \(\Delta\ge0\)
\(\Leftrightarrow4m+5\ge0\Leftrightarrow m\ge-\dfrac{5}{4}\)
Theo viet ta có
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(2m+1\right)}{1}=2m+1\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{m^2-1}{1}=m^2-1\end{matrix}\right.\)
Do \(x_1\) là nghiệm của phương trình \(\left(1\right)\) nên
\(x_1^2-\left(2m+1\right)x_1+m^2-1=0\)
\(\Leftrightarrow x_1^2=\left(2m+1\right)x_1-m^2+1\) \(\left(2\right)\)
Thay \(\left(2\right)\) vào \(\left(x_1^2-2mx_1+m^2\right)\left(x_2+1\right)=4\)
ta được \(\left[\left(2m+1\right)x_1-m^2+1-2mx_1+m^2\right]\left(x_2+1\right)=4\)
\(\Leftrightarrow\left(x_1+1\right)\left(x_2+1\right)=4\)
\(\Leftrightarrow x_1x_2+x_1+x_2+1=4\)
\(\Leftrightarrow m^2-1+2m+1+1=4\)
\(\Leftrightarrow m^2+2m-3=0\) \(\left(3\right)\)
Giải phương trình ta được \(m_1=1\) (Thỏa điều kiện)\(;\)
\(m_2=-3\) (Không thỏa điều kiện)
Vậy \(m=1\)

Gọi \(a,b,c\) là ba số cần tìm.
Theo đề bài ta có:
\(a+b+c=420\)
\(\dfrac{6}{7}\cdot a=\dfrac{9}{11}\cdot b=\dfrac{2}{3}\cdot c\)
\(\Rightarrow\dfrac{18a}{21}=\dfrac{18b}{22}=\dfrac{18c}{27}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được
\(\dfrac{18a}{21}=\dfrac{18b}{22}=\dfrac{18c}{27}=\dfrac{18a+18b+18c}{21+22+27}=\dfrac{18\left(a+b+c\right)}{70}=\dfrac{18\cdot420}{70}=108\)
* \(\dfrac{18a}{21}=108\Rightarrow a=126\)
* \(\dfrac{18b}{22}=108\Rightarrow b=132\)
* \(\dfrac{18c}{27}=108\Rightarrow c=162\)
Vậy ba số cần tìm là \(126;132;162\)

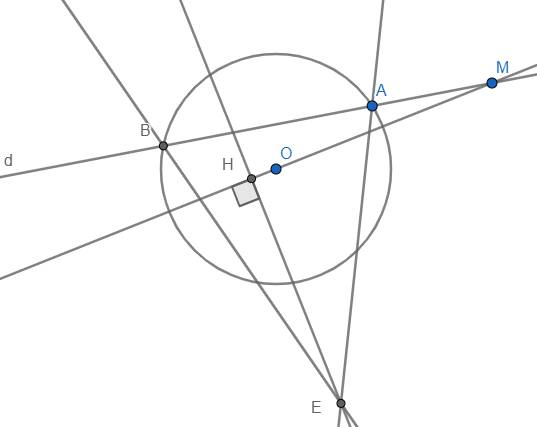
Gọi \(F\) là giao điểm của \(AB\) và \(EI\)
Xét \(\Delta IAF\) và \(\Delta ICE\)
có: \(\widehat{IAF}=\widehat{ICE}=90^o\left(gt\right)\)
      \(IA=IC\left(gt\right)\)
      \(\widehat{AIF}=\widehat{CIE}\) (đối đỉnh)
\(\Rightarrow\Delta IAF=\Delta ICE\left(g-c-g\right)\)
\(\Rightarrow IF=IE\) (hai cạnh tương ứng)
Xét tứ giác \(AFCE\)
có: \(IA=IC\left(gt\right)\)
      \(IF=IE\left(cmt\right)\)
\(\Rightarrow\) Tứ giác \(AFCE\) là hình bình hành
\(\Rightarrow AE//FC\left(1\right)\)
Xét \(\Delta BFC\)
có: \(CI\perp BF\left(gt\right)\)
      \(FI\perp BC\left(gt\right)\)
\(\Rightarrow I\) là trực tâm của \(\Delta BFC\)
\(\Rightarrow BI\perp FC\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow AE\perp BI\left(đpcm\right)\)

\(9999=99\times101=909\times11=33\times303=9999\times1\)

Ta thấy: \(2024\equiv1\) (\(mod\) \(2023\))
\(20242024\equiv1909\) (\(mod\) \(2023\))
...
\(2024...2024:2023\) dư một số nào đó là một trong các số từ \(1\) đến \(2022\) (\(2023\) số).
* Xét \(2024\) số: \(2024;20242024;...;20242024...2024\) (Gồm \(2024\) bộ số \(2024\))
 + Lấy \(2024\) số trên chia cho \(2023\), ta có \(2024\) số dư từ \(0\) đến \(2022\).
\(\Rightarrow\) Tồn tại hai số chia cho \(2023\) có cùng số dư.
Giả sử hai số đó là \(a=2024...2024\) (\(i\) bộ số \(2024\)) và \(b=2024...2024\) (\(j\) bộ số \(2024\)) \(\left(1\le i\le j\le2024\right)\)
+ \(a-b=2024...2024\cdot10^{4i}\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\)
+ \(ƯCLN\left(10^{4i};2023\right)=1\)
\(\Rightarrow2024...2024\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\) \(\left(đpcm\right)\).

+ \(x-y-z=0\)
\(\Rightarrow\dfrac{x}{x}-\dfrac{\left(y+z\right)}{x}=0\) (Do \(x\ne0\))
\(\Leftrightarrow1-\dfrac{y+z}{x}=0\)
+ \(x-y-z=0\)
\(\Rightarrow\dfrac{\left(x-z\right)}{y}-\dfrac{y}{y}=0\) (Do \(y\ne0\))
\(\Leftrightarrow1-\dfrac{x-z}{y}=0\)
+ \(x-y-z=0\)
\(\Rightarrow\dfrac{\left(x-y\right)}{z}-\dfrac{z}{z}=0\) (Do \(z\ne0\))
\(\Leftrightarrow1-\dfrac{x-y}{z}=0\)
Ta có: \(B=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\)
\(=\left(1-\dfrac{x}{y}-\dfrac{z}{x}+\dfrac{zx}{xy}\right)\left(1+\dfrac{y}{z}\right)\)
\(=\left(1-\dfrac{x}{y}-\dfrac{z}{x}+\dfrac{z}{y}\right)\left(1+\dfrac{y}{z}\right)\)
\(=1+\dfrac{y}{z}-\dfrac{x}{y}-\dfrac{xy}{yz}-\dfrac{z}{x}-\dfrac{zy}{xz}+\dfrac{z}{y}+\dfrac{zy}{yz}\)
\(=1-\dfrac{y+z}{x}+1-\dfrac{x-z}{y}+1-\dfrac{x-y}{z}-1\)
\(=-1\)
Vậy \(B=-1\)

\(x^4-3x+2=\left(x-1\right)\left(x^3+ax^2+bx-2\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x^3+x^2+x-2\right)=\left(x-1\right)\left(x^3+ax^2+bx-2\right)\)
\(\Rightarrow x^3+x^2+x-2=x^3+ax^2+bx-2\)
\(\Rightarrow1\cdot x^2+1\cdot x=ax^2+bx\)
\(\Rightarrow a=1\) và \(b=1\)